What Is 4/20 As A Percent
Kalali
Mar 29, 2025 · 4 min read
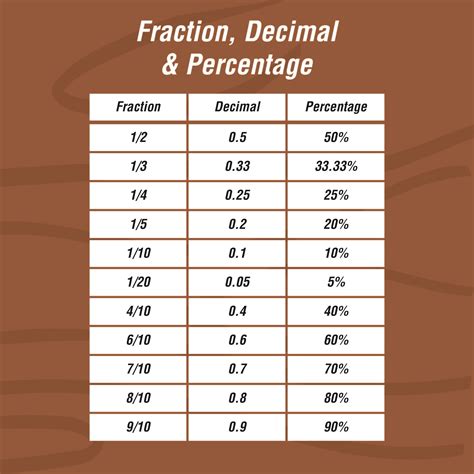
Table of Contents
What is 4/20 as a Percent? A Comprehensive Guide
The simple fraction 4/20 might seem insignificant at first glance, but understanding its percentage equivalent opens doors to a wider world of mathematical applications. This guide will explore not just the answer, but also the underlying principles of converting fractions to percentages, providing you with a solid foundation for future calculations. We'll delve into various methods, real-world examples, and address common misconceptions.
Understanding Fractions and Percentages
Before diving into the calculation, let's establish a clear understanding of the terms involved.
Fractions: A fraction represents a part of a whole. It's expressed as a ratio of two numbers – the numerator (top number) and the denominator (bottom number). In our case, 4/20 means 4 parts out of a total of 20 parts.
Percentages: A percentage is a fraction expressed as a portion of 100. It uses the "%" symbol to denote its value relative to a whole. For instance, 50% means 50 parts out of 100, or half.
Method 1: Simplifying the Fraction
The simplest method to convert 4/20 to a percentage involves simplifying the fraction first. This makes the subsequent conversion to a percentage much easier.
Simplifying 4/20
Both the numerator (4) and the denominator (20) are divisible by 4. Dividing both by 4, we get:
4 ÷ 4 = 1 20 ÷ 4 = 5
This simplifies the fraction to 1/5.
Converting 1/5 to a Percentage
To convert a fraction to a percentage, we need to express it as a fraction with a denominator of 100. We can achieve this by multiplying both the numerator and denominator by 20:
(1 × 20) / (5 × 20) = 20/100
Therefore, 1/5 is equal to 20/100, which is equivalent to 20%.
Method 2: Direct Conversion Using Division
Another approach is to directly convert the original fraction 4/20 into a decimal and then into a percentage.
Converting the Fraction to a Decimal
Divide the numerator (4) by the denominator (20):
4 ÷ 20 = 0.2
This gives us the decimal equivalent of 4/20.
Converting the Decimal to a Percentage
To convert a decimal to a percentage, multiply the decimal by 100 and add the "%" symbol:
0.2 × 100 = 20%
Therefore, using this method also confirms that 4/20 is equal to 20%.
Method 3: Using Proportions
This method utilizes the concept of proportions to solve for the percentage.
We can set up a proportion:
4/20 = x/100
Where 'x' represents the percentage we're trying to find.
To solve for 'x', we can cross-multiply:
20x = 400
Now, divide both sides by 20:
x = 400 ÷ 20 = 20
Therefore, x = 20, confirming that 4/20 is equal to 20%.
Real-World Applications of Percentage Conversions
Understanding percentage conversions isn't just about mathematical exercises; it has practical applications in numerous real-world scenarios:
-
Calculating Discounts: If a store offers a 20% discount on an item, knowing how to convert percentages to fractions or decimals is crucial for determining the final price.
-
Understanding Interest Rates: Interest rates on loans, savings accounts, and investments are usually expressed as percentages.
-
Analyzing Data: In fields like statistics and data analysis, percentages are extensively used to represent proportions and trends within data sets.
-
Financial Reporting: Businesses use percentages to present their financial performance, including profit margins, revenue growth, and expense ratios.
-
Scientific Research: Percentages are often used to represent experimental results and statistical significance.
Common Misconceptions and Troubleshooting
While the conversion of 4/20 to a percentage is straightforward, certain misconceptions can lead to errors:
-
Incorrect Simplification: Failing to simplify the fraction before conversion can complicate the process and increase the chance of errors. Always simplify fractions where possible.
-
Misplacing the Decimal Point: When converting decimals to percentages, ensure you multiply by 100 and not 10 or 1000.
-
Confusing Numerator and Denominator: It's crucial to remember that the numerator is divided by the denominator when converting a fraction to a decimal.
Expanding Your Knowledge: Working with More Complex Fractions
The principles applied to 4/20 can be extended to more complex fractions. The steps remain consistent: simplify the fraction (if possible), convert it to a decimal through division, and then multiply the decimal by 100 to obtain the percentage.
Conclusion: Mastering Percentage Conversions
Converting fractions like 4/20 to percentages is a fundamental skill with far-reaching applications. By mastering the various methods outlined in this guide—simplification, direct division, and proportions—you can confidently tackle percentage calculations in various contexts. Remember to always double-check your work and be mindful of common errors to ensure accuracy. With practice, you'll become proficient in converting fractions to percentages, enhancing your problem-solving skills and enriching your understanding of mathematical concepts. This knowledge will prove invaluable across various disciplines and in your everyday life.
Latest Posts
Latest Posts
-
Cual Es El 20 Por Ciento De 20
Mar 31, 2025
-
Organisms That Make Their Own Food
Mar 31, 2025
-
What Percent Of 40 Is 15
Mar 31, 2025
-
How Many Calories In A 1 Gram Of Fat
Mar 31, 2025
-
Cuanto Es 100 Pies En Metros
Mar 31, 2025
Related Post
Thank you for visiting our website which covers about What Is 4/20 As A Percent . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
