What Is 4 7 As A Percent
Kalali
Apr 13, 2025 · 5 min read
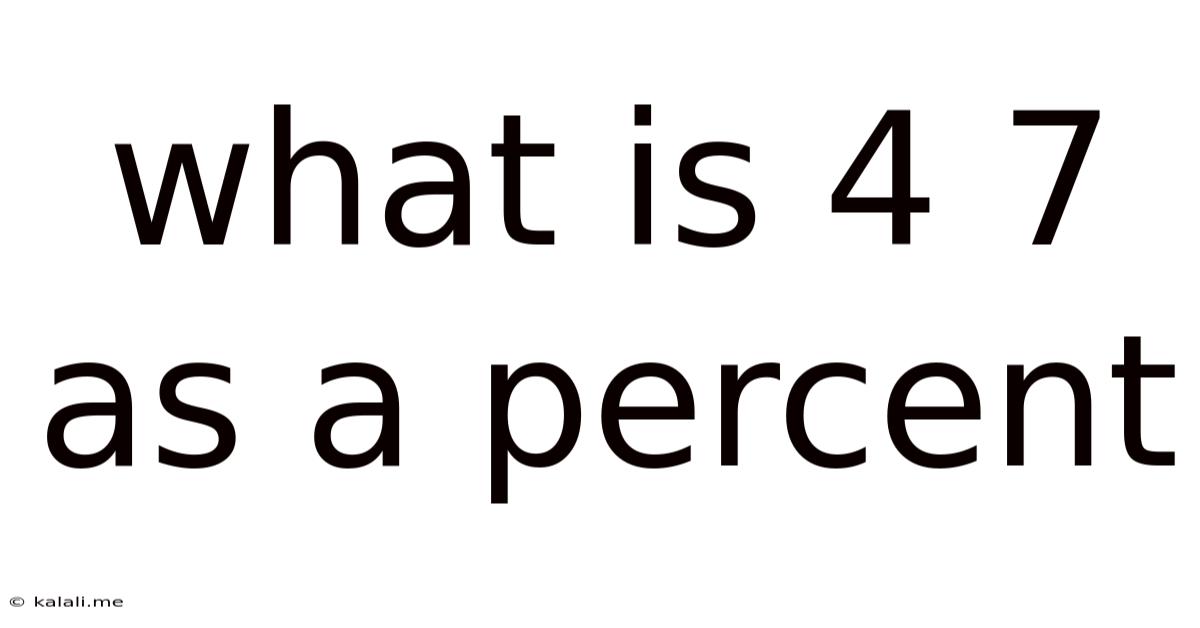
Table of Contents
What is 4/7 as a Percent? A Comprehensive Guide to Fraction-to-Percentage Conversion
This article delves deep into the process of converting fractions to percentages, specifically focusing on how to express 4/7 as a percentage. We'll not only calculate the answer but also explore the underlying mathematical principles and provide practical applications and examples. Understanding this conversion is crucial for various fields, from everyday calculations to advanced statistical analysis. We'll cover different methods, ensuring you gain a thorough understanding of this important mathematical concept.
Meta Description: Learn how to convert the fraction 4/7 into a percentage. This comprehensive guide explains the process step-by-step, explores different methods, and provides practical applications. Master fraction-to-percentage conversion with this detailed tutorial.
Understanding Fractions and Percentages
Before diving into the conversion of 4/7, let's establish a solid understanding of fractions and percentages.
A fraction represents a part of a whole. It's expressed as a ratio of two numbers, the numerator (top number) and the denominator (bottom number). The numerator indicates the number of parts you have, while the denominator indicates the total number of parts in the whole.
A percentage, on the other hand, represents a fraction of 100. It indicates the proportion of something relative to 100. The symbol "%" represents "per hundred" or "out of 100."
The relationship between fractions and percentages is fundamental. A percentage is simply a fraction with a denominator of 100. Therefore, converting a fraction to a percentage involves finding an equivalent fraction with a denominator of 100.
Method 1: The Direct Division Method
This is the most straightforward method for converting a fraction to a percentage. It involves dividing the numerator by the denominator and then multiplying the result by 100.
Steps:
-
Divide the numerator by the denominator: 4 ÷ 7 ≈ 0.5714
-
Multiply the result by 100: 0.5714 × 100 ≈ 57.14
Therefore, 4/7 is approximately 57.14%.
Method 2: Finding an Equivalent Fraction with a Denominator of 100
This method involves manipulating the fraction to obtain an equivalent fraction with a denominator of 100. While this method might seem more complex initially, it provides a deeper understanding of the underlying concept.
Unfortunately, we cannot directly convert 4/7 into an equivalent fraction with a denominator of 100 using simple multiplication. 100 is not divisible by 7 without a remainder.
Method 3: Using Proportions
Proportions offer a powerful and versatile way to convert fractions to percentages. A proportion is a statement that two ratios are equal. We can set up a proportion to solve for the percentage equivalent.
Let 'x' represent the percentage equivalent of 4/7. We can set up the proportion:
4/7 = x/100
To solve for 'x', we can cross-multiply:
7x = 400
x = 400/7
x ≈ 57.14
Therefore, 4/7 is approximately 57.14%.
Understanding the Remainder and Rounding
Notice that in all the methods above, we've obtained an approximate value. This is because 4/7 is a non-terminating decimal; it continues infinitely. We need to round the result to a specific number of decimal places to express it as a percentage. Commonly, we round to two decimal places, resulting in 57.14%. However, depending on the context and required level of accuracy, you might round to a different number of decimal places.
Practical Applications of Fraction-to-Percentage Conversion
Converting fractions to percentages has numerous applications across various fields:
-
Finance: Calculating interest rates, discounts, and profit margins often involves converting fractions to percentages. For example, a store offering a 1/4 discount on an item is offering a 25% discount.
-
Statistics: Expressing data as percentages makes it easier to understand and compare. For instance, if a survey shows 4 out of 7 people prefer a certain product (4/7), we can express this as approximately 57.14% preference.
-
Science: In scientific experiments and data analysis, percentages are frequently used to represent proportions and probabilities.
-
Everyday Life: Many everyday situations require converting fractions to percentages. For example, determining the percentage of a task completed or calculating the percentage of ingredients in a recipe.
Advanced Concepts: Working with Percentages in Calculations
Understanding how to convert fractions to percentages is crucial for more complex calculations involving percentages:
-
Calculating percentage increase or decrease: Suppose a value increases from 20 to 25. The increase is 5. To find the percentage increase, we express the increase (5) as a fraction of the original value (20): 5/20 = 1/4 = 25%.
-
Finding the original value given a percentage: If a product is on sale for 75% of its original price, and the sale price is $60, we can set up an equation to find the original price: 0.75x = 60. Solving for 'x' will give us the original price.
-
Calculating compound interest: This involves calculating interest on both the principal amount and accumulated interest. Understanding percentages is essential for solving compound interest problems.
Conclusion: Mastering Fraction-to-Percentage Conversion
Converting fractions to percentages is a fundamental mathematical skill with broad applications. By understanding the different methods – direct division, finding equivalent fractions, and using proportions – you can effectively convert any fraction to its percentage equivalent. Remembering to round appropriately based on the context is also crucial. This comprehensive guide provides a solid foundation for mastering this essential skill, equipping you to handle a wide range of percentage-based problems and applications in various fields. Consistent practice will reinforce your understanding and enable you to tackle these conversions with confidence. From everyday calculations to more advanced mathematical problems, the ability to convert fractions to percentages is an invaluable asset.
Latest Posts
Latest Posts
-
How To Beat Stage 9 On Bloxorz
Jul 05, 2025
-
How Many Cups Of Sugar In A Five Pound Bag
Jul 05, 2025
-
What Do You Call A Palace Window Answer Key
Jul 05, 2025
-
How Many Quarts In A 5 Gallon Bucket
Jul 05, 2025
-
How Far Is The Closest Ocean Beach To Me
Jul 05, 2025
Related Post
Thank you for visiting our website which covers about What Is 4 7 As A Percent . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.