What Is 4 Divided By 1 2
Kalali
Apr 18, 2025 · 5 min read
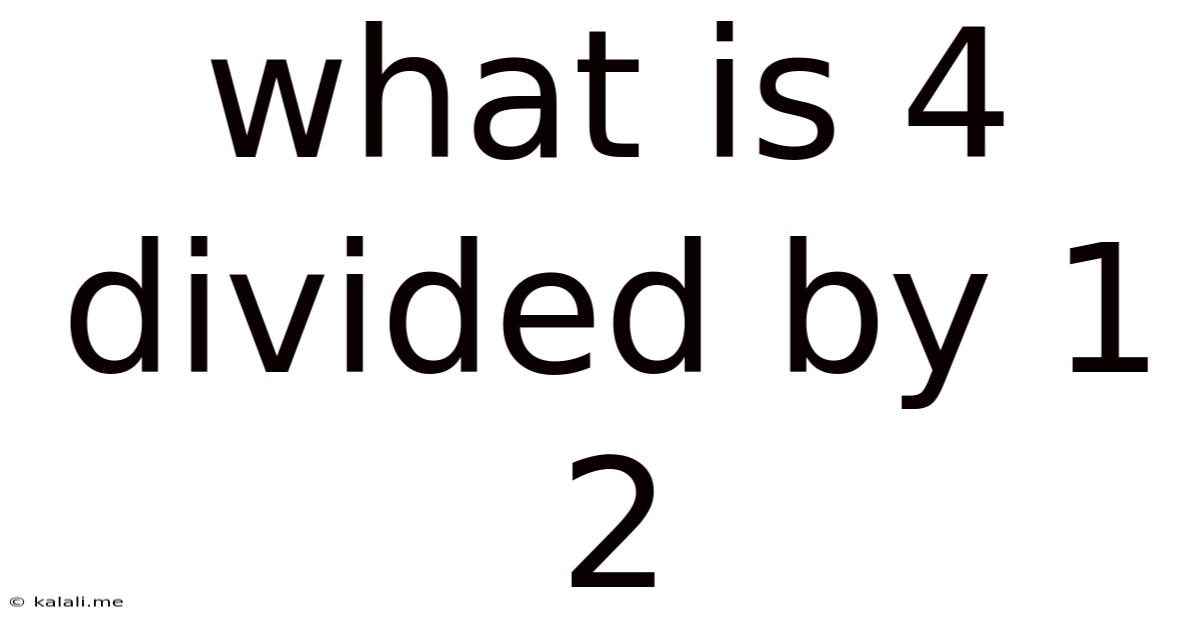
Table of Contents
What is 4 Divided by 1/2? Understanding Fractions and Division
The seemingly simple question, "What is 4 divided by 1/2?", often trips up students and even adults. It highlights a crucial misunderstanding of how fractions interact with division. The answer isn't 2, as many initially assume. In fact, the answer is 8. This article will delve deep into the reason behind this, exploring the underlying concepts of fractions, division, and how to solve similar problems confidently. We'll move beyond simple memorization and build a solid understanding of the mathematical principles involved.
Understanding the Problem: The Conceptual Hurdle
The difficulty stems from the inherent nature of division and the representation of fractions. Division asks, "How many times does one number fit into another?" When we divide 4 by 2, we're asking how many times 2 fits into 4. The answer, intuitively, is 2. But when we introduce a fraction like 1/2, the intuition falters. We're now asking, "How many times does 1/2 fit into 4?"
This isn't immediately obvious. It requires a shift in perspective, moving away from the whole number approach and embracing the fractional world. To clarify, let's visualize this. Imagine you have four pizzas. If you divide each pizza in half (1/2), you'll end up with eight slices. Therefore, 1/2 fits into 4 a total of eight times.
Methods for Solving 4 ÷ 1/2
There are several approaches to solving this division problem, each offering a different perspective on the underlying mathematics.
1. The Reciprocal Method (Inverting and Multiplying)
This is the most common and efficient method for dividing by fractions. The rule states: to divide by a fraction, invert the fraction (flip the numerator and denominator) and multiply.
Therefore, 4 ÷ 1/2 becomes 4 x 2/1, which simplifies to 4 x 2 = 8. This method is based on the fundamental properties of fractions and division. When you invert a fraction and multiply, you're essentially performing the inverse operation of division, leading to the correct result.
2. The Visual Method (Using Models)
This approach emphasizes understanding through visualization. As mentioned earlier, imagine four pizzas. Dividing each pizza in half gives you eight slices. Each slice represents 1/2. Therefore, there are eight halves in four wholes. This method is particularly helpful for beginners, providing a concrete representation of the abstract concept. You can apply this method to other similar division problems involving fractions. For instance, try visualizing 6 divided by 1/3. How many thirds are there in six wholes?
3. The Repeated Subtraction Method
This method focuses on the definition of division as repeated subtraction. How many times can you subtract 1/2 from 4 before you reach 0?
- 4 - 1/2 = 3 1/2
- 3 1/2 - 1/2 = 3
- 3 - 1/2 = 2 1/2
- 2 1/2 - 1/2 = 2
- 2 - 1/2 = 1 1/2
- 1 1/2 - 1/2 = 1
- 1 - 1/2 = 1/2
- 1/2 - 1/2 = 0
Counting the number of subtractions, we arrive at the answer: 8. This method is more time-consuming than the reciprocal method, but it reinforces the meaning of division.
Extending the Understanding: Working with Different Fractions and Whole Numbers
The principles discussed above apply equally to other division problems involving fractions. Let's examine a few more examples:
-
6 ÷ 1/3: Using the reciprocal method, this becomes 6 x 3/1 = 18. Visually, imagine six pizzas, each divided into thirds. You would have 18 slices (thirds).
-
10 ÷ 2/5: Using the reciprocal method, this becomes 10 x 5/2 = 50/2 = 25.
-
3/4 ÷ 1/2: This involves dividing a fraction by a fraction. Using the reciprocal method, this becomes 3/4 x 2/1 = 6/4 = 3/2 or 1 1/2.
Common Mistakes to Avoid
Several common mistakes can lead to incorrect answers when dividing by fractions. Understanding these mistakes is crucial to mastering the concept.
-
Simply subtracting the numerator and denominator: This is incorrect. Division with fractions requires using the reciprocal method or a similar approach.
-
Multiplying straight across: This is also incorrect. You need to invert the fraction you're dividing by before multiplying.
-
Forgetting to simplify: Always simplify your answer to its lowest terms. For instance, 6/4 should be simplified to 3/2 or 1 1/2.
Practical Applications and Real-World Examples
Understanding division with fractions isn't just an academic exercise; it has numerous practical applications in everyday life.
-
Cooking and Baking: Recipes often require dividing ingredients into fractions. Knowing how to divide by fractions ensures accurate measurements.
-
Construction and Engineering: Dividing materials and measurements in construction and engineering projects often involves fractions. Accurate calculations are essential for precise results.
-
Sewing and Crafting: Projects often require dividing lengths of fabric or other materials into fractions.
-
Data Analysis: Many data analysis tasks involve working with fractions and decimals, making the ability to accurately divide by fractions essential for correct interpretation.
Conclusion: Mastering Fraction Division
The question "What is 4 divided by 1/2?" serves as a gateway to understanding a crucial aspect of mathematics. By mastering the methods presented – the reciprocal method, the visual method, and the repeated subtraction method – and avoiding common errors, you’ll build a solid foundation in fraction division. This understanding transcends the classroom, providing valuable tools for navigating various aspects of daily life and more advanced mathematical concepts. Remember, consistent practice and a focus on understanding the underlying principles are key to success. Don't just memorize the rules; understand why they work. This will enable you to tackle more complex problems with confidence and accuracy. The ability to confidently and correctly divide by fractions is a valuable skill that will serve you well in numerous contexts.
Latest Posts
Latest Posts
-
25 Is What Percent Of 65
Apr 19, 2025
-
How Many Ounces In 2 1 2 Quarts
Apr 19, 2025
-
17 Is What Percent Of 68
Apr 19, 2025
-
How Big Is 36 Inches In Feet
Apr 19, 2025
-
40 Celsius Is What In Fahrenheit
Apr 19, 2025
Related Post
Thank you for visiting our website which covers about What Is 4 Divided By 1 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.