What Is 4 Percent Of 10000
Kalali
Apr 17, 2025 · 5 min read
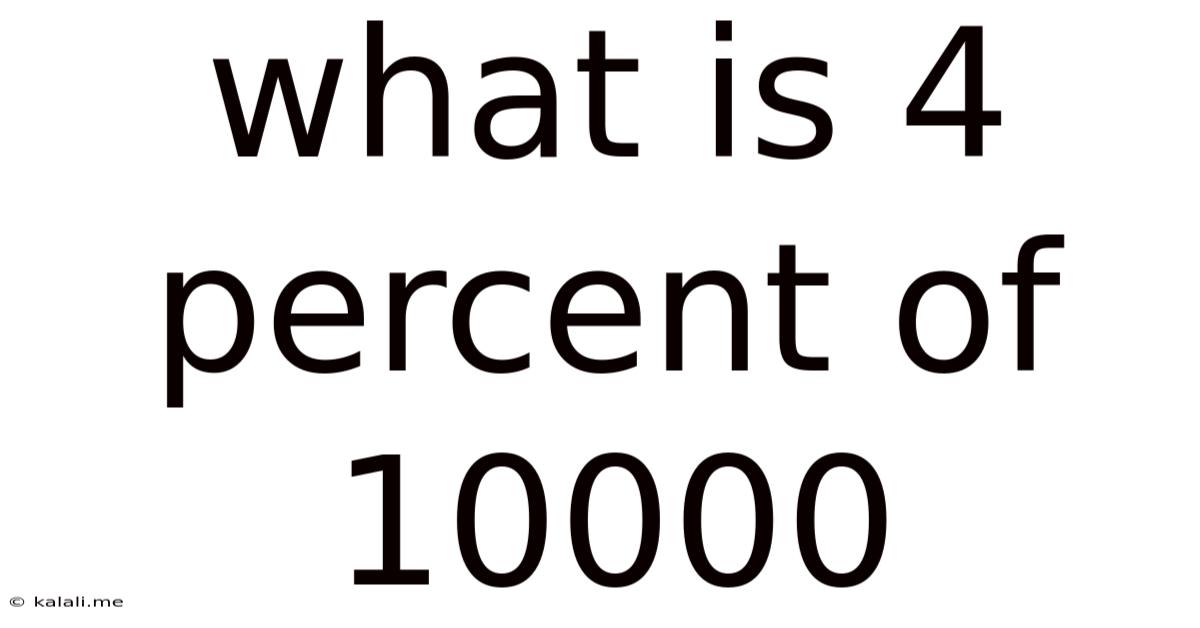
Table of Contents
What is 4 Percent of 10000? A Comprehensive Guide to Percentage Calculations
What is 4 percent of 10000? This seemingly simple question opens the door to understanding a fundamental concept in mathematics and its widespread applications in various fields. This article will not only answer this specific question but also delve into the broader topic of percentage calculations, providing you with the tools and knowledge to tackle similar problems with confidence. We'll explore different methods for calculating percentages, discuss real-world examples, and even touch upon the importance of percentages in financial literacy.
Understanding Percentages:
A percentage is a way of expressing a number as a fraction of 100. The word "percent" literally means "out of one hundred." The symbol "%" is used to represent percentages. For example, 50% means 50 out of 100, which is equivalent to the fraction 50/100 or the decimal 0.5.
Calculating 4% of 10000:
There are several methods to calculate 4% of 10000. Let's explore the most common approaches:
Method 1: Using the Decimal Equivalent:
This is perhaps the most straightforward method. We first convert the percentage to its decimal equivalent by dividing it by 100. 4% divided by 100 is 0.04. Then, we multiply this decimal by the number we're interested in: 10000.
Therefore: 0.04 * 10000 = 400
So, 4% of 10000 is $\boxed{400}$.
Method 2: Using Fractions:
Percentages can also be expressed as fractions. 4% can be written as 4/100. To find 4% of 10000, we multiply 10000 by the fraction 4/100:
(4/100) * 10000 = 4 * (10000/100) = 4 * 100 = 400
Again, we arrive at the answer: 4% of 10000 is $\boxed{400}$.
Method 3: Using Proportions:
Proportions offer another effective way to solve percentage problems. We can set up a proportion:
x / 10000 = 4 / 100
To solve for x (4% of 10000), we cross-multiply:
100x = 40000
x = 40000 / 100
x = 400
Once more, the answer is $\boxed{400}$.
Real-World Applications of Percentage Calculations:
Understanding percentage calculations is crucial in numerous real-world situations. Here are a few examples:
-
Finance: Calculating interest on loans, savings accounts, and investments heavily relies on percentage calculations. For instance, if you invest $10,000 and earn a 5% annual return, your earnings will be 0.05 * $10,000 = $500. This understanding is critical for financial planning and making informed investment decisions. Discount rates in shopping, sales tax calculations, and understanding your income tax bracket also involve percentages.
-
Statistics: Percentages are fundamental in statistical analysis, allowing researchers to represent data proportions and trends effectively. For instance, expressing survey results as percentages makes it easier to comprehend the distribution of opinions or preferences. Analyzing market share, population growth, and even the success rate of medical treatments frequently uses percentage representation.
-
Science: Percentages are prevalent in scientific research and reporting. Expressing experimental error rates, success rates of clinical trials, or the concentration of solutions frequently uses percentage notation. Understanding these percentages is crucial for interpreting scientific findings and drawing valid conclusions.
-
Everyday Life: From calculating tips in restaurants (e.g., a 15% tip on a $50 bill) to understanding sales discounts (e.g., a 20% off sale), percentage calculations are woven into our daily lives. Even determining the nutritional content of food often relies on percentages of daily recommended values.
Beyond the Basics: More Complex Percentage Problems:
While calculating 4% of 10000 is relatively straightforward, percentage problems can become more complex. Here are some examples:
-
Finding the percentage: Instead of finding a percentage of a number, you might need to determine what percentage one number is of another. For example, what percentage of 500 is 100? This involves dividing 100 by 500 and multiplying the result by 100: (100/500) * 100 = 20%.
-
Finding the original value: You might know the percentage increase or decrease and the final value, and need to determine the original value. For example, if a price increased by 10% to $110, what was the original price? This requires working backward using the percentage change formula.
-
Compound percentages: Compound interest, where interest is calculated not only on the principal amount but also on accumulated interest, involves more complex percentage calculations. These problems require understanding exponential growth or decay.
Tips for Mastering Percentage Calculations:
-
Practice regularly: The key to mastering percentage calculations is consistent practice. Solve various problems, starting with simple ones and gradually increasing the complexity.
-
Use different methods: Try all the methods discussed above (decimal, fraction, and proportion) to see which works best for you. Understanding different approaches enhances your flexibility and problem-solving skills.
-
Check your work: After solving a problem, always check your answer to ensure accuracy. A simple way to do this is to estimate the answer first and then compare it to your calculated result. Significant discrepancies should prompt you to double-check your steps.
-
Utilize online calculators: While learning the principles is essential, online percentage calculators can be helpful for verification or when dealing with particularly complex calculations.
Conclusion:
The answer to "What is 4 percent of 10000?" is 400. However, this seemingly simple question opens the door to understanding a vast and important concept in mathematics with wide-ranging real-world applications. By grasping the fundamental principles of percentage calculations, and through consistent practice, you'll develop valuable problem-solving skills applicable to finance, statistics, science, and countless everyday situations. Remember to practice regularly, explore different methods, and always check your work to ensure accuracy. Mastering percentages is a valuable asset, enhancing your numerical fluency and empowering you to tackle more complex mathematical challenges. From financial literacy to scientific understanding, the ability to confidently work with percentages is a skill that will serve you well throughout your life.
Latest Posts
Latest Posts
-
What Is The Prefix Of In
Apr 19, 2025
-
The Ability Of A Substance To Catch Fire Or Burn
Apr 19, 2025
-
35 8 As A Mixed Number
Apr 19, 2025
-
What Is The Domain Of The Function Graphed Below
Apr 19, 2025
-
What Is 6 Ft 1 In Cm
Apr 19, 2025
Related Post
Thank you for visiting our website which covers about What Is 4 Percent Of 10000 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.