What Is 4 To The Power Of 0
Kalali
Apr 17, 2025 · 5 min read
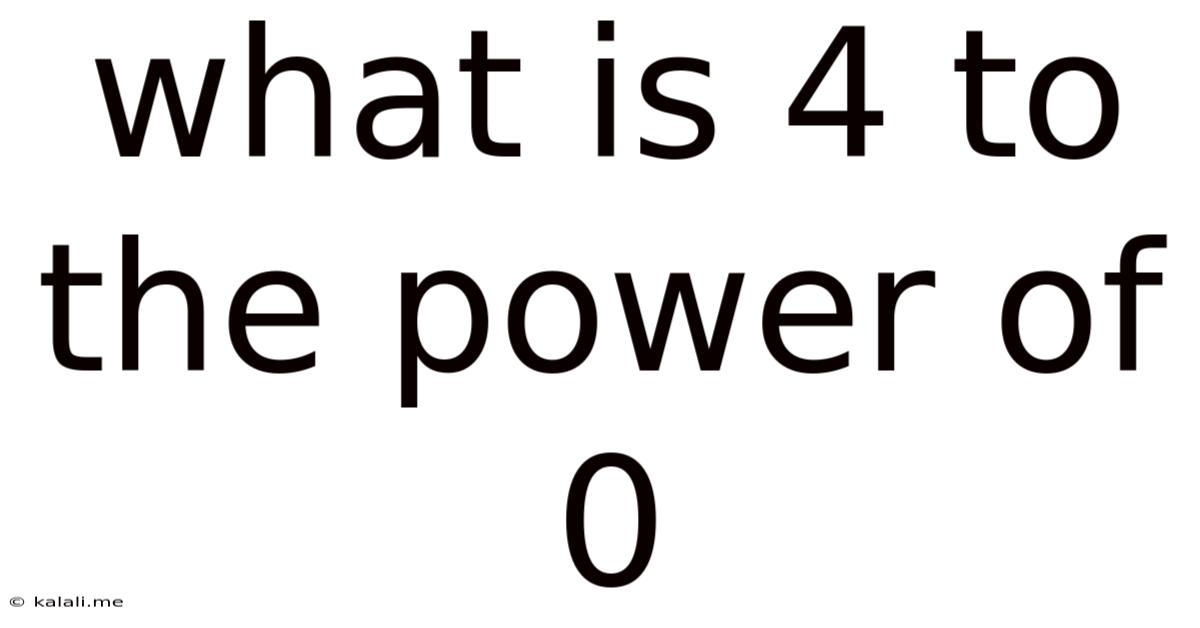
Table of Contents
What is 4 to the Power of 0? Unraveling the Mystery of Exponents
What is 4<sup>0</sup>? This seemingly simple question can trip up even seasoned mathematicians if they're not careful. The answer, surprisingly, is 1. But why? This article delves deep into the fascinating world of exponents, exploring the logic and rules behind this seemingly counter-intuitive result. We'll explore various approaches to understanding this concept, from the rules of exponents to the practical applications of this mathematical principle. Understanding this foundational concept is crucial for anyone pursuing higher-level mathematics, computer science, or any field dealing with exponential growth or decay.
Understanding Exponents: A Quick Recap
Before we tackle 4<sup>0</sup>, let's refresh our understanding of exponents. An exponent, also known as a power or index, indicates how many times a number (the base) is multiplied by itself. For instance:
- 4<sup>1</sup> = 4 (4 multiplied by itself once)
- 4<sup>2</sup> = 16 (4 multiplied by itself twice, 4 x 4)
- 4<sup>3</sup> = 64 (4 multiplied by itself three times, 4 x 4 x 4)
- 4<sup>4</sup> = 256 (4 multiplied by itself four times, 4 x 4 x 4 x 4)
Notice a pattern? As the exponent increases by 1, the result is multiplied by the base (4, in this case).
The Pattern and the Zero Exponent
Let's continue this pattern in reverse. Dividing by the base each time, we observe:
- 4<sup>4</sup> = 256
- 4<sup>3</sup> = 64 (256 / 4)
- 4<sup>2</sup> = 16 (64 / 4)
- 4<sup>1</sup> = 4 (16 / 4)
Following this consistent pattern, what would 4<sup>0</sup> be? It would be 4<sup>1</sup> divided by 4, which equals 1 (4 / 4 = 1). This consistent pattern provides a strong intuitive argument for why any number (except 0) raised to the power of 0 equals 1.
The Rule of Exponents: a<sup>m</sup> / a<sup>n</sup> = a<sup>m-n</sup>
Another way to approach this is through the fundamental rule of exponents: when dividing two exponential terms with the same base, you subtract the exponents. Let's apply this rule to our example:
Let's consider 4<sup>2</sup> / 4<sup>2</sup>. Using the rule above:
4<sup>2</sup> / 4<sup>2</sup> = 4<sup>2-2</sup> = 4<sup>0</sup>
However, we also know that any number divided by itself equals 1. Therefore:
4<sup>2</sup> / 4<sup>2</sup> = 16 / 16 = 1
Thus, since 4<sup>2</sup> / 4<sup>2</sup> equals both 4<sup>0</sup> and 1, we can conclude that 4<sup>0</sup> = 1. This algebraic manipulation provides a solid mathematical justification for the rule. This approach holds true for any non-zero base.
The Empty Product
In mathematics, the empty product is a concept that explains this phenomenon. The empty product is the result of multiplying no numbers together. In standard multiplication, multiplying by 1 doesn't change the value. Similarly, raising a number to the power of zero can be interpreted as the empty product; you're not multiplying the base by itself at all. The multiplicative identity is 1; therefore, the result of the empty product is 1. This provides another perspective on why 4<sup>0</sup> equals 1.
Why 0<sup>0</sup> is Undefined
It's crucial to distinguish that while any non-zero number raised to the power of zero is 1, 0<sup>0</sup> is undefined. This is because it leads to a contradiction. Consider the conflicting patterns:
- Any number to the power of zero is 1.
- Zero to any positive power is zero.
These conflicting rules make 0<sup>0</sup> an indeterminate form. Its value depends on the context in which it arises. Therefore, it is not assigned a single definitive value.
Applications of Exponents and the Zero Exponent Rule
The concept of exponents, including the rule for a zero exponent, is fundamental in numerous fields. Here are a few examples:
-
Science: Exponential growth and decay are ubiquitous in scientific models. Population growth, radioactive decay, and compound interest are all described using exponential functions. The zero exponent represents the starting point or initial condition in these models.
-
Computer Science: Binary systems, a cornerstone of computing, rely on powers of 2. Understanding exponents is crucial for tasks such as bit manipulation, memory allocation, and algorithm analysis.
-
Finance: Compound interest calculations rely heavily on exponents. The zero exponent represents the initial investment amount before any interest is accrued.
-
Engineering: Exponential functions appear in many engineering applications, such as signal processing, control systems, and modeling physical phenomena.
-
Mathematics: Exponents are essential throughout higher mathematics, appearing in calculus, linear algebra, and complex analysis. The zero exponent rule is a foundational building block for more advanced mathematical concepts.
Common Misconceptions and Clarifications
Several misconceptions often surround the concept of 4<sup>0</sup> (and indeed, any number raised to the power of zero). Let's address some of them:
-
Zero to the power of zero is not one: As discussed earlier, 0<sup>0</sup> is undefined. This is a crucial point to remember to avoid mathematical errors.
-
It's not about multiplication: While the exponent represents repeated multiplication, the zero exponent doesn't involve any multiplication. It's a consequence of the consistent patterns observed in the exponent rules.
-
The rule is consistent: The rule that any non-zero number raised to the power of zero equals one holds consistently across all mathematical fields.
Conclusion: The Significance of 4<sup>0</sup> = 1
The seemingly simple equation 4<sup>0</sup> = 1 underpins a profound understanding of exponents and their mathematical behavior. By exploring various perspectives, including the pattern of dividing by the base, the rule of exponents, the concept of the empty product, and addressing common misconceptions, we’ve solidified our comprehension of this foundational mathematical concept. This seemingly simple rule forms the backbone of countless applications across numerous fields, highlighting its significance in both theoretical and practical contexts. Understanding the ‘why’ behind 4<sup>0</sup>=1 is not just a matter of rote memorization; it's a key to unlocking a deeper understanding of the powerful world of exponents and their widespread applications.
Latest Posts
Latest Posts
-
Cuanto Es 50 Yardas En Metros
Apr 19, 2025
-
How Many Liters Is 70 Ounces
Apr 19, 2025
-
What Is The End Product Of Transcription
Apr 19, 2025
-
Cuanto Es 38 Centimetros En Pulgadas
Apr 19, 2025
-
How Many Fluid Ounces In 1 3 Cup
Apr 19, 2025
Related Post
Thank you for visiting our website which covers about What Is 4 To The Power Of 0 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.