What Is 4 To The Power Of 5
Kalali
Apr 16, 2025 · 6 min read
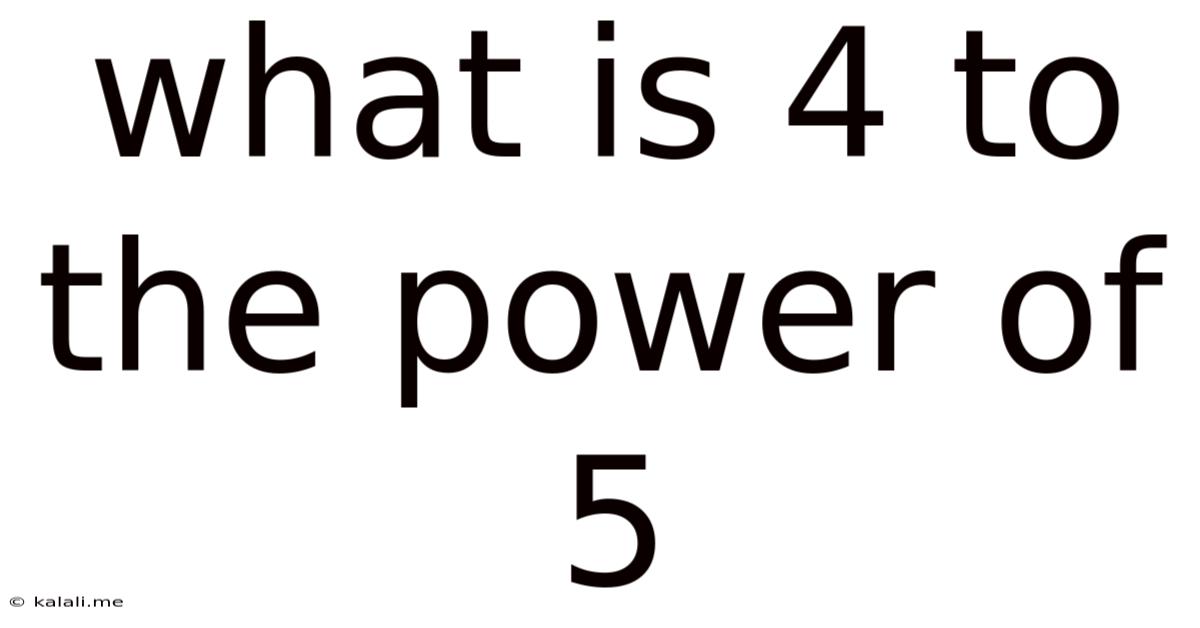
Table of Contents
What is 4 to the Power of 5? A Deep Dive into Exponentiation and its Applications
What is 4 to the power of 5? The simple answer is 1024. But this seemingly straightforward mathematical problem opens a door to a fascinating world of exponentiation, its properties, applications, and even its historical context. This article will not only answer the initial question but also explore the broader concept of exponents, demonstrating their importance in various fields, from simple calculations to complex scientific modeling. We'll delve into practical examples and explore why understanding exponents is crucial in our increasingly data-driven world.
Meta Description: Discover the answer to "What is 4 to the power of 5?" and delve into the world of exponents. This comprehensive guide explores exponentiation's properties, applications in various fields, and its significance in mathematics and beyond.
Understanding Exponents: A Foundation
Before we delve into the specifics of 4<sup>5</sup>, let's establish a firm understanding of exponentiation. An exponent, also known as a power or index, indicates how many times a base number is multiplied by itself. In the expression b<sup>n</sup>, 'b' represents the base, and 'n' represents the exponent. Therefore, 4<sup>5</sup> means 4 multiplied by itself five times: 4 × 4 × 4 × 4 × 4.
This seemingly simple concept forms the basis for many advanced mathematical concepts and has far-reaching implications in numerous fields. Understanding exponents is essential for anyone working with:
- Data analysis: Exponential growth and decay are frequently observed in datasets related to population growth, financial investments, and radioactive decay.
- Computer science: Exponents are fundamental to binary systems, algorithms, and data structures.
- Physics and engineering: Exponential functions model various physical phenomena, such as radioactive decay, capacitor discharge, and population dynamics.
- Finance: Compound interest calculations heavily rely on exponential functions.
Calculating 4 to the Power of 5: Step-by-Step
Now, let's explicitly calculate 4<sup>5</sup>:
- Start with the base: Our base is 4.
- Apply the exponent: The exponent is 5, meaning we multiply the base by itself five times.
- The calculation: 4 × 4 × 4 × 4 × 4 = 1024
Therefore, 4 to the power of 5 is 1024.
Beyond the Calculation: Exploring Properties of Exponents
Understanding the calculation is only the first step. The real power of exponents lies in their properties, which allow for efficient simplification and manipulation of expressions. Some key properties include:
- Product of powers: When multiplying two numbers with the same base, you add the exponents: b<sup>m</sup> × b<sup>n</sup> = b<sup>m+n</sup>. For example, 4<sup>2</sup> × 4<sup>3</sup> = 4<sup>2+3</sup> = 4<sup>5</sup> = 1024.
- Quotient of powers: When dividing two numbers with the same base, you subtract the exponents: b<sup>m</sup> ÷ b<sup>n</sup> = b<sup>m-n</sup>. For example, 4<sup>5</sup> ÷ 4<sup>2</sup> = 4<sup>5-2</sup> = 4<sup>3</sup> = 64.
- Power of a power: When raising a power to another power, you multiply the exponents: (b<sup>m</sup>)<sup>n</sup> = b<sup>m×n</sup>. For example, (4<sup>2</sup>)<sup>3</sup> = 4<sup>2×3</sup> = 4<sup>6</sup> = 4096.
- Power of a product: The power of a product is the product of the powers: (ab)<sup>n</sup> = a<sup>n</sup>b<sup>n</sup>. For example, (2×2)<sup>5</sup> = 2<sup>5</sup> × 2<sup>5</sup> = 32 × 32 = 1024.
- Power of a quotient: The power of a quotient is the quotient of the powers: (a/b)<sup>n</sup> = a<sup>n</sup>/b<sup>n</sup>. For example, (4/2)<sup>5</sup> = 4<sup>5</sup>/2<sup>5</sup> = 1024/32 = 32.
Understanding these properties allows for significant simplification of complex exponential expressions. This is particularly valuable in algebraic manipulation and problem-solving.
Applications of Exponents in Real-World Scenarios
Exponents are not merely abstract mathematical concepts; they are essential tools with wide-ranging practical applications:
1. Compound Interest: Compound interest calculations rely heavily on exponential functions. The formula for compound interest is A = P(1 + r/n)^(nt), where:
- A = the future value of the investment/loan, including interest
- P = the principal investment amount (the initial deposit or loan amount)
- r = the annual interest rate (decimal)
- n = the number of times that interest is compounded per year
- t = the number of years the money is invested or borrowed for
Understanding exponential growth in this context allows individuals to accurately predict the future value of their investments or the total amount to be repaid on a loan.
2. Population Growth: Exponential functions accurately model population growth (under ideal conditions). If a population grows at a constant rate, its size after a certain period can be predicted using an exponential equation. This is crucial for urban planning, resource allocation, and environmental management.
3. Radioactive Decay: Radioactive materials decay exponentially. The half-life of a radioactive substance is the time it takes for half of the material to decay. This concept is crucial in various fields, including nuclear physics, archaeology (carbon dating), and medicine (radiotherapy).
4. Computer Science: Binary numbers, the foundation of computer systems, utilize powers of 2. For example, 2<sup>8</sup> (256) represents the number of possible values in a single byte. Understanding exponents is fundamental to comprehending data storage, memory management, and various computer algorithms.
5. Scientific Modeling: Exponentials are extensively used in scientific modeling to represent various phenomena, including:
- Epidemiological modeling: Predicting the spread of infectious diseases.
- Chemical kinetics: Studying reaction rates.
- Fluid dynamics: Analyzing fluid flow.
- Quantum mechanics: Describing the behavior of subatomic particles.
Negative and Fractional Exponents
The concept of exponents extends beyond positive integers. Negative exponents represent reciprocals, while fractional exponents represent roots.
- Negative exponents: b<sup>-n</sup> = 1/b<sup>n</sup>. For example, 4<sup>-2</sup> = 1/4<sup>2</sup> = 1/16.
- Fractional exponents: b<sup>m/n</sup> = <sup>n</sup>√b<sup>m</sup>. For example, 4<sup>3/2</sup> = √(4<sup>3</sup>) = √64 = 8.
These extensions of the concept of exponents allow for even greater flexibility and power in mathematical modeling and problem-solving.
Conclusion: The Significance of Understanding Exponents
We started with the simple question, "What is 4 to the power of 5?" and found the answer to be 1024. However, this journey has taken us far beyond a single calculation. We have explored the fundamental concept of exponentiation, its properties, and its far-reaching applications across numerous disciplines. From understanding compound interest to modeling population growth and radioactive decay, the ability to work with exponents is crucial in navigating our increasingly complex world. The importance of a strong understanding of this mathematical concept cannot be overstated, offering a powerful tool for problem-solving and a deeper appreciation of the patterns and processes governing our universe. Mastering exponents is not just about numbers; it's about unlocking a deeper understanding of the world around us.
Latest Posts
Latest Posts
-
What Is 1 8 Of 100
Apr 19, 2025
-
What Is 25 Fahrenheit In Celsius
Apr 19, 2025
-
What Percent Of 500 Is 400
Apr 19, 2025
-
How Many Cups Is 20 Fl Oz
Apr 19, 2025
Related Post
Thank you for visiting our website which covers about What Is 4 To The Power Of 5 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.