What Is 40 Percent Of 40
Kalali
Mar 08, 2025 · 5 min read
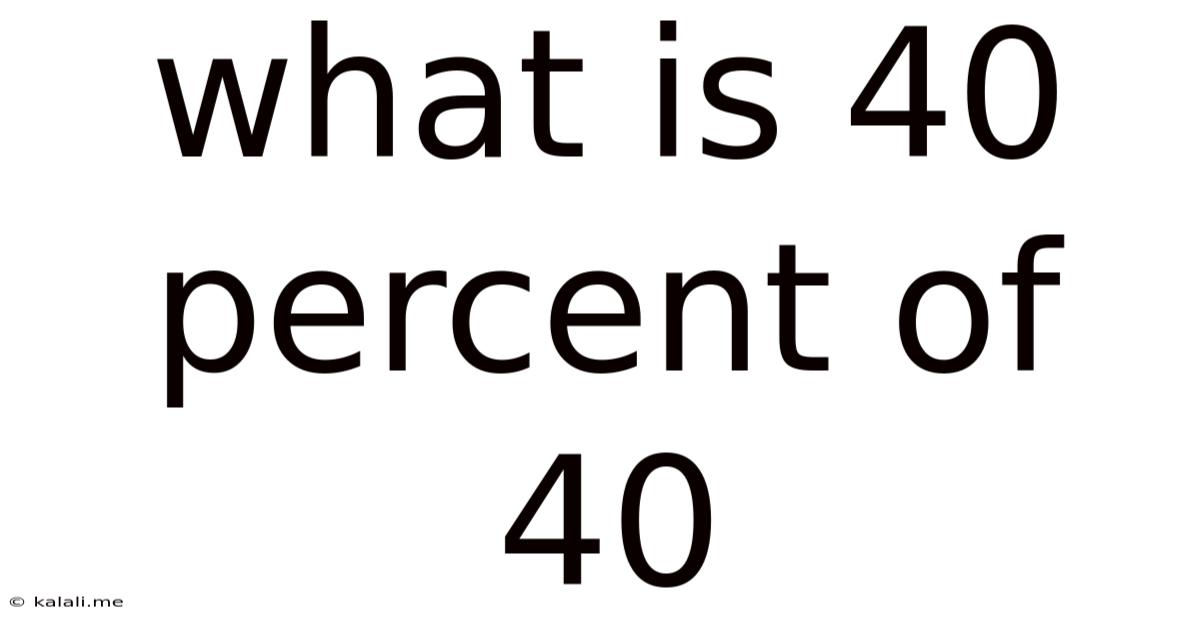
Table of Contents
What is 40 Percent of 40? A Deep Dive into Percentages and Their Applications
Calculating percentages is a fundamental skill applicable across numerous aspects of life, from everyday budgeting and shopping to complex financial modeling and scientific analysis. Understanding how to calculate percentages effectively empowers you to make informed decisions, interpret data accurately, and solve a wide range of problems. This article will explore the seemingly simple question, "What is 40 percent of 40?" but will delve much deeper, providing a comprehensive understanding of percentage calculations, their practical applications, and the underlying mathematical principles.
Understanding Percentages: The Basics
A percentage is simply a fraction expressed as a part of 100. The term "percent" literally means "per hundred" or "out of one hundred." For example, 40% means 40 out of 100, which can be written as the fraction 40/100 or the decimal 0.40. This representation allows for easy comparison and calculation across different values.
Converting Percentages to Decimals and Fractions:
To perform calculations with percentages, it's often easier to convert them to their decimal or fraction equivalents. This is a straightforward process:
- Percentage to Decimal: Divide the percentage by 100. For example, 40% becomes 40 ÷ 100 = 0.40.
- Percentage to Fraction: Write the percentage as the numerator over 100 as the denominator. Then simplify the fraction if possible. For example, 40% becomes 40/100, which simplifies to 2/5.
Calculating 40 Percent of 40: The Step-by-Step Approach
Now, let's tackle the core question: What is 40 percent of 40? We can solve this using several methods:
Method 1: Using the Decimal Equivalent
- Convert the percentage to a decimal: 40% = 0.40
- Multiply the decimal by the number: 0.40 x 40 = 16
Therefore, 40 percent of 40 is $\boxed{16}$.
Method 2: Using the Fraction Equivalent
- Convert the percentage to a fraction: 40% = 40/100 = 2/5
- Multiply the fraction by the number: (2/5) x 40 = (2 x 40) / 5 = 80/5 = 16
Again, we arrive at the answer: 40 percent of 40 is $\boxed{16}$.
Method 3: Proportions
This method is particularly useful when dealing with more complex percentage problems. We can set up a proportion:
- Let 'x' represent 40% of 40.
- We can write the proportion as: x/40 = 40/100
- Cross-multiply: 100x = 40 x 40
- Solve for x: 100x = 1600 => x = 1600/100 = 16
Thus, 40 percent of 40 is $\boxed{16}$.
Real-World Applications of Percentage Calculations
The ability to calculate percentages extends far beyond simple arithmetic exercises. Here are some examples of how percentage calculations are used in daily life and professional settings:
1. Finance and Budgeting:
- Calculating discounts: Understanding discounts allows you to determine the actual price of items after a percentage reduction. For example, a 20% discount on a $100 item means a saving of $20.
- Calculating interest: Interest on loans, savings accounts, and investments is often expressed as a percentage. Knowing how to calculate interest helps you manage your finances effectively.
- Analyzing financial statements: Percentage changes in revenue, expenses, and profits are crucial for analyzing business performance and making strategic decisions.
- Calculating taxes: Sales tax, income tax, and other taxes are frequently expressed as percentages of the base amount.
2. Shopping and Sales:
- Comparing prices: Percentages help compare prices of different items, especially when considering discounts or sales.
- Understanding unit pricing: Unit pricing, often expressed as a percentage, allows for efficient comparison of prices per unit of weight or volume.
3. Science and Statistics:
- Analyzing data: Percentages are commonly used to represent proportions and trends in data analysis, scientific research, and statistical reports.
- Calculating probabilities: Probability, a fundamental concept in statistics, is often expressed as a percentage.
- Determining experimental error: Percentage error helps assess the accuracy of experimental results.
4. Healthcare:
- Calculating medication dosages: Precise percentage calculations are crucial in determining appropriate medication dosages.
- Analyzing health statistics: Percentages are used to represent disease prevalence, treatment success rates, and other vital health indicators.
5. Real Estate:
- Calculating commission: Real estate agents' commissions are usually a percentage of the property's sale price.
- Calculating property taxes: Property taxes are often calculated as a percentage of the assessed value of the property.
Beyond the Basics: More Complex Percentage Problems
While calculating 40% of 40 is relatively straightforward, many real-world percentage problems involve more complex scenarios. Here are some examples:
- Finding the percentage increase or decrease: This involves calculating the percentage change between two values. For example, if a stock price increased from $50 to $60, the percentage increase is 20%.
- Calculating the original value after a percentage change: This involves working backward from a final value and a percentage change to find the original value. For example, if a price increased by 10% to $110, the original price was $100.
- Calculating percentage points: A percentage point represents an absolute difference in percentages, not a percentage change. For example, an increase from 10% to 20% is a 10 percentage point increase, but a 100% percentage increase.
Mastering Percentages: Tips and Tricks
To master percentage calculations and enhance your problem-solving skills, consider these tips:
- Practice regularly: The more you practice, the more comfortable and efficient you will become.
- Use different methods: Experiment with different approaches to solving percentage problems, such as using decimals, fractions, or proportions. This will help you choose the most appropriate method depending on the specific problem.
- Understand the underlying concepts: A strong grasp of the mathematical principles behind percentages is essential for solving complex problems.
- Use online calculators and resources: Many online calculators and resources can assist you with percentage calculations. However, always strive to understand the underlying principles to avoid over-reliance on these tools.
- Break down complex problems into smaller steps: This makes the process manageable and reduces the risk of errors.
Conclusion: The Power of Percentages
The seemingly simple question, "What is 40 percent of 40?" serves as a gateway to understanding the broad applicability of percentage calculations. From everyday financial transactions to complex scientific analysis, percentages are a cornerstone of numerical literacy. Mastering the ability to calculate and interpret percentages empowers you to make informed decisions, analyze data critically, and succeed in various aspects of life. By understanding the underlying principles and practicing regularly, you can unlock the full potential of percentages and use them effectively to solve a vast array of problems.
Latest Posts
Latest Posts
-
How Many Bunnies Are There In The World
Jun 30, 2025
-
How Is A Watch And Ruler Similar
Jun 30, 2025
-
How Many Liters Is In A Water Bottle
Jun 30, 2025
-
How Many Cups Of Milk Are In A Half Gallon
Jun 30, 2025
-
How Many Ritz Crackers In A Cup
Jun 30, 2025
Related Post
Thank you for visiting our website which covers about What Is 40 Percent Of 40 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.