What Is 45 Out Of 50 As A Percentage
Kalali
Mar 08, 2025 · 5 min read
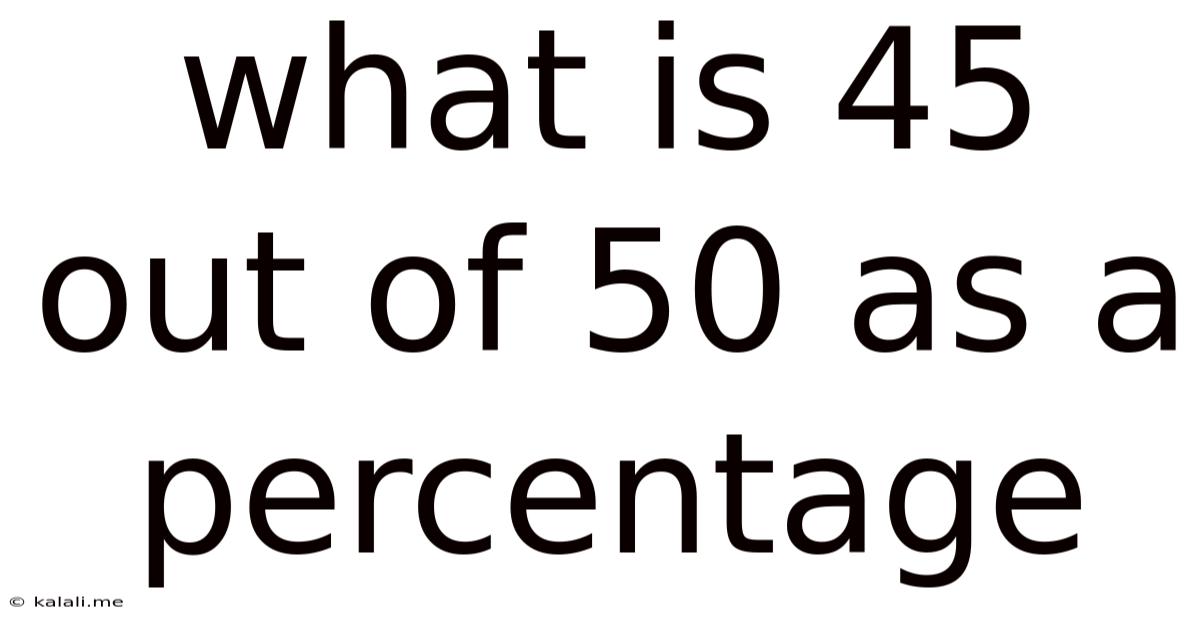
Table of Contents
What is 45 out of 50 as a Percentage? A Comprehensive Guide
Calculating percentages is a fundamental skill with widespread applications in various aspects of life, from academic assessments and financial transactions to everyday decision-making. Understanding how to convert fractions into percentages is crucial for interpreting data, comparing values, and making informed choices. This comprehensive guide will delve into the specifics of determining what 45 out of 50 represents as a percentage, along with exploring the underlying principles and offering practical examples to solidify your understanding.
Understanding Percentages: The Basics
A percentage is a way of expressing a number as a fraction of 100. The word "percent" itself comes from the Latin "per centum," meaning "out of a hundred." This means that any percentage can be represented as a fraction with a denominator of 100. For instance, 50% is equivalent to 50/100, which simplifies to 1/2. Understanding this fundamental concept is key to mastering percentage calculations.
Calculating 45 out of 50 as a Percentage: Step-by-Step
To determine what 45 out of 50 represents as a percentage, we can follow a simple three-step process:
Step 1: Formulate the Fraction
The first step involves expressing the given information as a fraction. In this case, we have 45 out of 50, which is written as 45/50.
Step 2: Convert the Fraction to a Decimal
To convert a fraction to a decimal, we divide the numerator (the top number) by the denominator (the bottom number). In this case, we divide 45 by 50:
45 ÷ 50 = 0.9
Step 3: Convert the Decimal to a Percentage
To convert a decimal to a percentage, we multiply the decimal by 100 and add the percent symbol (%).
0.9 x 100 = 90%
Therefore, 45 out of 50 is equal to 90%.
Alternative Methods for Percentage Calculation
While the above method is straightforward, there are alternative approaches to calculate percentages, each offering unique advantages depending on the context and individual preferences.
Method 1: Using Proportions
This method involves setting up a proportion to solve for the unknown percentage. We can represent the problem as:
45/50 = x/100
To solve for x (the percentage), we cross-multiply:
50x = 4500
x = 4500/50
x = 90
Therefore, x = 90%, confirming our previous result.
Method 2: Using a Calculator
Most calculators have a percentage function that simplifies the calculation process. Simply enter 45 ÷ 50 and then multiply the result by 100 to obtain the percentage. This method is particularly efficient for more complex calculations.
Method 3: Simplifying the Fraction First
Before performing the division, you can simplify the fraction 45/50 by dividing both the numerator and the denominator by their greatest common divisor (GCD), which is 5:
45/5 = 9 50/5 = 10
This simplifies the fraction to 9/10. Now, divide 9 by 10:
9 ÷ 10 = 0.9
Finally, multiply by 100 to convert the decimal to a percentage:
0.9 x 100 = 90%
This method reduces the complexity of the division, especially when dealing with larger numbers.
Practical Applications of Percentage Calculations
The ability to calculate percentages is vital in numerous real-world situations. Here are some examples:
- Academic Performance: Calculating the percentage of correct answers on a test or exam is crucial for determining grades and assessing understanding.
- Financial Matters: Understanding percentages is essential for calculating interest rates, discounts, taxes, tips, and investment returns. Calculating percentage change in stock prices is a key component of financial analysis.
- Data Analysis: Percentages are frequently used to represent data in charts, graphs, and reports, providing a clear and concise way to illustrate trends and patterns. For example, understanding market share often involves interpreting percentages.
- Sales and Marketing: Businesses use percentages to track sales performance, analyze conversion rates, and measure the effectiveness of marketing campaigns. Discount percentages are a crucial element of pricing strategies.
- Everyday Life: Calculating percentages helps in comparing prices, understanding discounts, and making informed decisions about purchases.
Expanding on the Concept: Percentage Increase and Decrease
Beyond simple percentage calculations, it's essential to understand how to calculate percentage increases and decreases. These concepts are frequently encountered in various fields, from finance to statistics.
Percentage Increase: This involves determining the percentage change when a value increases. The formula for percentage increase is:
[(New Value - Old Value) / Old Value] x 100%
Percentage Decrease: This involves determining the percentage change when a value decreases. The formula for percentage decrease is:
[(Old Value - New Value) / Old Value] x 100%
Let's consider an example: Suppose a product's price increased from $50 to $60. The percentage increase would be:
[(60 - 50) / 50] x 100% = 20%
Conversely, if the price decreased from $60 to $50, the percentage decrease would be:
[(60 - 50) / 60] x 100% ≈ 16.67%
Advanced Percentage Applications and Considerations
The applications of percentage calculations extend far beyond basic computations. More advanced scenarios might involve:
- Compound Interest: This involves calculating interest on both the principal amount and accumulated interest, resulting in exponential growth.
- Statistical Analysis: Percentages play a key role in statistical analysis, used to represent proportions, probabilities, and confidence intervals.
- Financial Modeling: Creating financial models often requires extensive use of percentage calculations to forecast revenue, expenses, and profitability.
Conclusion
Understanding how to calculate percentages is a crucial skill with far-reaching implications. This guide has provided a detailed explanation of how to determine what 45 out of 50 represents as a percentage (90%), along with alternative methods and practical applications. By mastering these concepts, you will be well-equipped to handle a wide range of quantitative problems and make informed decisions in various aspects of your life. Remember to practice regularly to solidify your understanding and build confidence in your ability to work with percentages effectively. The ability to confidently and accurately work with percentages will undoubtedly enhance your analytical skills and problem-solving abilities.
Latest Posts
Latest Posts
-
How Many Cups Of Milk Are In A Half Gallon
Jun 30, 2025
-
How Many Ritz Crackers In A Cup
Jun 30, 2025
-
How Many 16 9 Oz Bottles Make A Half Gallon
Jun 30, 2025
-
How Many Times Does 3 Go Into 24
Jun 30, 2025
-
What Year Was I Born If Im 15
Jun 30, 2025
Related Post
Thank you for visiting our website which covers about What Is 45 Out Of 50 As A Percentage . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.