What Is 5/7 As A Percent
Kalali
Apr 10, 2025 · 5 min read
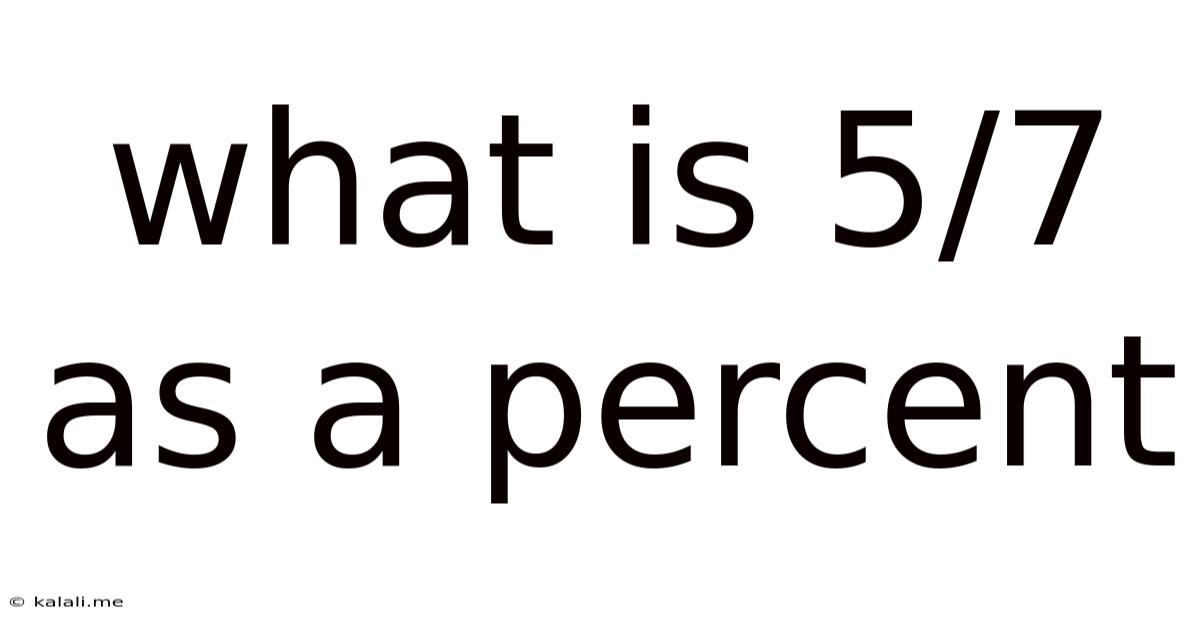
Table of Contents
What is 5/7 as a Percent? A Comprehensive Guide to Fraction-to-Percentage Conversion
This article will delve into the process of converting the fraction 5/7 into a percentage, exploring not only the calculation itself but also the underlying mathematical principles and practical applications. We'll also cover various methods for performing this conversion, catering to different levels of mathematical understanding. Understanding fraction-to-percentage conversion is crucial for various applications, from calculating discounts and interest rates to interpreting data presented in different formats. By the end of this comprehensive guide, you'll not only know the answer to "What is 5/7 as a percent?" but also possess a strong foundational understanding of percentage calculations.
Understanding Fractions and Percentages
Before diving into the specifics of converting 5/7 to a percentage, let's briefly review the concepts of fractions and percentages.
-
Fractions: A fraction represents a part of a whole. It's expressed as a ratio of two numbers, the numerator (top number) and the denominator (bottom number). The numerator indicates the number of parts you have, while the denominator indicates the total number of parts in the whole. In our case, 5/7 means we have 5 parts out of a total of 7 parts.
-
Percentages: A percentage is a way of expressing a number as a fraction of 100. The symbol "%" represents "per cent," meaning "out of one hundred." For example, 50% means 50 out of 100, which is equivalent to the fraction 50/100 or 1/2.
Method 1: Direct Conversion using Division
The most straightforward method to convert a fraction to a percentage involves two simple steps:
-
Divide the numerator by the denominator: In our case, we divide 5 by 7: 5 ÷ 7 ≈ 0.7142857
-
Multiply the result by 100: This converts the decimal to a percentage. 0.7142857 × 100 ≈ 71.42857%
Therefore, 5/7 is approximately 71.43%. The slight rounding is necessary because the decimal representation of 5/7 is non-terminating (it goes on forever without repeating).
Method 2: Finding an Equivalent Fraction with a Denominator of 100
This method is particularly useful when dealing with fractions that can be easily converted to an equivalent fraction with a denominator of 100. While not directly applicable to 5/7 (as 7 doesn't divide evenly into 100), understanding this approach provides valuable insight into the concept of percentage.
To illustrate, let's consider the fraction 1/4. To convert it to a percentage, we need to find an equivalent fraction with a denominator of 100. We can multiply both the numerator and denominator by 25:
(1 × 25) / (4 × 25) = 25/100
Since 25/100 means 25 out of 100, the percentage is 25%. This method directly reveals the percentage without needing a separate multiplication by 100.
Method 3: Using Proportions
The concept of proportions offers a more formal mathematical approach to fraction-to-percentage conversion. We can set up a proportion:
5/7 = x/100
Where 'x' represents the percentage we are trying to find. To solve for 'x', we cross-multiply:
7x = 500
x = 500/7 ≈ 71.43
Therefore, 5/7 is approximately 71.43%.
Understanding the Decimal Approximation
It's important to emphasize that the percentage we calculated (71.43%) is an approximation. The true value of 5/7 as a decimal is a non-terminating, non-repeating decimal. This means it continues infinitely without a repeating pattern. Rounding to two decimal places (71.43%) is a common practice for practical applications, offering sufficient accuracy for most purposes. However, depending on the context, you might need to use more decimal places for greater precision.
Practical Applications of Fraction-to-Percentage Conversion
The ability to convert fractions to percentages is crucial in various real-world scenarios:
-
Calculating Discounts: If a store offers a 2/5 discount on an item, you can convert 2/5 to a percentage to easily determine the discount amount.
-
Analyzing Data: Data presented in fractions can be more easily understood and compared when expressed as percentages. For example, comparing the success rate of two different marketing campaigns.
-
Financial Calculations: Interest rates, loan repayments, and investment returns are often expressed as percentages. Understanding the conversion between fractions and percentages is essential for managing personal finances.
-
Scientific and Engineering Applications: Percentages are commonly used to represent proportions and ratios in scientific experiments, engineering designs, and statistical analysis.
-
Everyday Calculations: Many everyday tasks, such as calculating tips, determining sale prices, or understanding survey results, involve working with percentages.
Advanced Concepts and Further Exploration
For those interested in a deeper understanding, exploring the following concepts can enhance your grasp of percentages and related mathematical concepts:
-
Recurring Decimals: Understanding recurring decimals, like the decimal representation of 5/7, is crucial for appreciating the limitations of rounding and the need for precision in certain contexts.
-
Percentage Change: Learning to calculate percentage increase and decrease is vital for analyzing trends and growth rates.
-
Compound Interest: Understanding how compound interest works involves working with percentages over time.
-
Statistical Analysis: Percentages play a significant role in various statistical analyses, including descriptive statistics, probability, and hypothesis testing.
Conclusion:
Converting 5/7 to a percentage involves dividing the numerator by the denominator and multiplying the result by 100. This results in an approximate value of 71.43%. While this is a straightforward calculation, understanding the underlying concepts of fractions, percentages, and decimal approximations is crucial for effectively applying this knowledge in various real-world situations. The methods outlined here – direct division, equivalent fractions, and proportions – provide diverse approaches to this fundamental mathematical conversion, catering to various levels of mathematical proficiency. The ability to confidently perform this conversion is a valuable skill with broad applicability across numerous fields and everyday life. Remember to consider the level of precision required for your specific application when choosing how many decimal places to round your answer to.
Latest Posts
Latest Posts
-
How Does The Monster Try To Gain Control Of Victor
Jul 14, 2025
-
Why Did The Cow Want A Divorce
Jul 14, 2025
-
Lowest Common Denominator For 3 4 5
Jul 14, 2025
-
Can You Be A Professor With A Masters
Jul 14, 2025
-
How Many Bottles Of Water Is 1 Liter
Jul 14, 2025
Related Post
Thank you for visiting our website which covers about What Is 5/7 As A Percent . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.