What Is 5 Percent Of 500
Kalali
Mar 06, 2025 · 5 min read
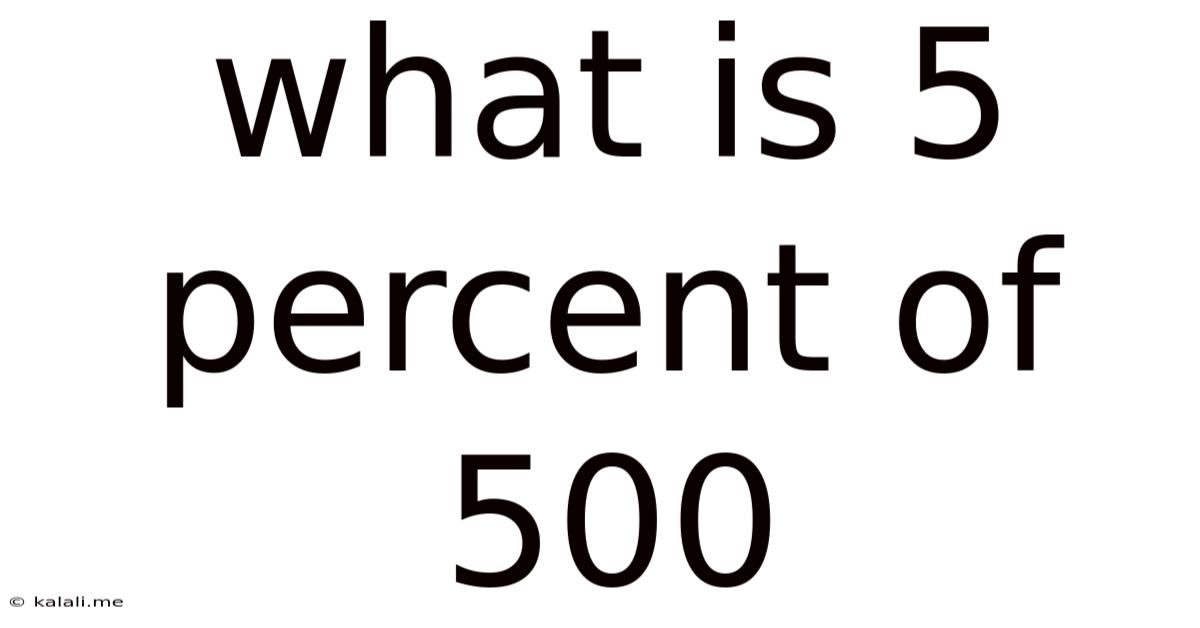
Table of Contents
What is 5 Percent of 500? A Deep Dive into Percentages and Their Applications
Calculating percentages is a fundamental skill applicable across numerous fields, from everyday budgeting and shopping to complex financial modeling and scientific analysis. Understanding how to determine percentages not only enhances your mathematical proficiency but also empowers you to make informed decisions in various aspects of your life. This article will thoroughly explore the calculation of "What is 5 percent of 500?" and delve into the broader concept of percentages, their real-world applications, and useful tips for mastering this crucial skill.
Understanding Percentages: A Foundation
A percentage is a way of expressing a number as a fraction of 100. The word "percent" literally means "per hundred," and it's represented by the symbol "%". Percentages provide a standardized method for comparing proportions and facilitating easy comprehension of relative values. For instance, saying "25% of the students passed the exam" is more intuitive than saying "one-quarter of the students passed the exam."
Key Concepts
Before tackling the calculation of 5% of 500, let's solidify some key percentage concepts:
-
Percentage as a Fraction: A percentage can be easily converted to a fraction by dividing the percentage by 100. For example, 5% is equivalent to 5/100, which simplifies to 1/20.
-
Percentage as a Decimal: Similarly, a percentage can be converted to a decimal by dividing the percentage by 100. 5% as a decimal is 0.05.
-
Finding a Percentage of a Number: This involves multiplying the number by the decimal equivalent of the percentage.
Calculating 5 Percent of 500: Three Methods
Now, let's address the core question: What is 5 percent of 500? We can use three common methods to arrive at the answer:
Method 1: Using the Fraction Method
-
Convert the percentage to a fraction: 5% = 5/100 = 1/20
-
Multiply the fraction by the number: (1/20) * 500 = 25
Therefore, 5% of 500 is 25.
Method 2: Using the Decimal Method
-
Convert the percentage to a decimal: 5% = 0.05
-
Multiply the decimal by the number: 0.05 * 500 = 25
This method reaffirms that 5% of 500 is indeed 25.
Method 3: Using the Proportion Method
This method involves setting up a proportion:
-
Let 'x' represent the unknown value (5% of 500): x/500 = 5/100
-
Cross-multiply: 100x = 5 * 500
-
Solve for 'x': 100x = 2500 => x = 2500/100 => x = 25
Once again, we find that 5% of 500 equals 25.
Real-World Applications of Percentage Calculations
The ability to calculate percentages is a valuable life skill with numerous practical applications:
1. Finance and Budgeting:
- Calculating discounts: Determining the price after a 20% discount on a $100 item.
- Understanding interest rates: Calculating simple and compound interest on loans and investments.
- Analyzing financial statements: Interpreting profit margins, return on investment (ROI), and other key financial metrics.
- Tax calculations: Determining the amount of income tax payable on your earnings.
- Tip calculations: Easily computing the appropriate tip amount in a restaurant.
2. Shopping and Sales:
- Comparing prices: Evaluating the best deals based on discounts and sales percentages.
- Calculating savings: Determining how much money you're saving on sale items.
3. Science and Statistics:
- Data analysis: Expressing data as percentages to illustrate trends and comparisons.
- Probability calculations: Determining the likelihood of events occurring.
4. Everyday Life:
- Cooking and baking: Adjusting ingredient quantities based on percentage increases or decreases in recipes.
- Understanding surveys and polls: Interpreting results expressed as percentages.
Tips for Mastering Percentage Calculations
Here are some helpful tips to enhance your proficiency in calculating percentages:
-
Practice Regularly: Consistent practice is key to mastering any mathematical skill. Work through various percentage problems to build your confidence and speed.
-
Utilize Calculators and Online Tools: While understanding the underlying concepts is crucial, calculators and online tools can be helpful, especially for complex calculations.
-
Memorize Common Percentage Equivalents: Familiarize yourself with the fraction and decimal equivalents of common percentages (e.g., 25% = 0.25 = 1/4, 50% = 0.5 = 1/2, 75% = 0.75 = 3/4). This will speed up your calculations.
-
Break Down Complex Problems: For intricate percentage problems, break them down into smaller, more manageable steps.
-
Check Your Work: Always double-check your answers to ensure accuracy. You can use different methods to verify your results.
Beyond the Basics: Advanced Percentage Applications
While calculating 5% of 500 is a straightforward example, percentage calculations can become more complex. Here are some advanced applications:
-
Percentage Change: Calculating the percentage increase or decrease between two values. For instance, if a stock price rises from $50 to $60, the percentage increase is calculated as: [(60-50)/50] * 100% = 20%.
-
Percentage Points: Understanding the difference between percentage change and percentage points is crucial in interpreting data. A change from 10% to 15% is a 5 percentage point increase, but a 50% increase relative to the initial 10%.
-
Compounding Percentages: This involves applying a percentage multiple times, commonly seen in interest calculations. For example, calculating the final amount after applying 5% interest annually for three years requires understanding compounding principles.
-
Weighted Averages: Calculating weighted averages using percentages is important in various fields, such as finance and statistics, where certain values carry more weight than others.
Conclusion: The Power of Percentages
Understanding percentages is a foundational skill with far-reaching applications in various aspects of life. The ability to accurately and efficiently calculate percentages empowers you to make informed decisions in personal finance, shopping, scientific analysis, and numerous other areas. Mastering percentage calculations not only enhances your mathematical proficiency but also equips you with a valuable tool for navigating the complexities of the modern world. From simple calculations like finding 5% of 500 to more advanced applications, the principles discussed in this article provide a solid foundation for your continued learning and application of percentages. Remember to practice regularly, utilize available tools, and break down complex problems into smaller, manageable steps. This consistent approach will help you build a strong understanding and confidence in tackling any percentage calculation you may encounter.
Latest Posts
Latest Posts
-
How Much Is 120 Kilograms In Pounds
Jul 12, 2025
-
Born In 1990 How Old Am I
Jul 12, 2025
-
What Is The Average Iq For A 5 Year Old
Jul 12, 2025
-
How Many 12 Oz Cups In A Gallon
Jul 12, 2025
-
How Much Older Is John The Baptist Than Jesus
Jul 12, 2025
Related Post
Thank you for visiting our website which covers about What Is 5 Percent Of 500 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.