What Is 5 To The Power Of 0
Kalali
Jul 28, 2025 · 5 min read
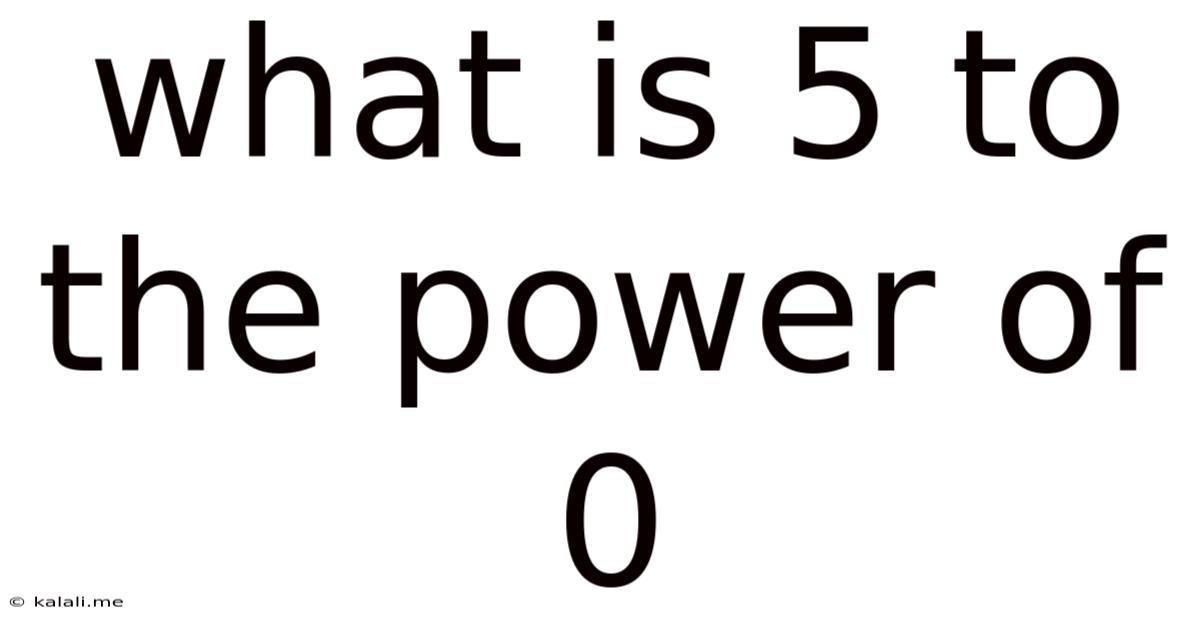
Table of Contents
What is 5 to the Power of 0? Unraveling the Mystery of Exponents
This seemingly simple question, "What is 5 to the power of 0?", often trips up students and even seasoned mathematicians when first encountered. The answer, surprisingly, is 1. But why is it 1? This article delves deep into the underlying mathematical principles, exploring various approaches to understand why any non-zero number raised to the power of zero equals one, providing a comprehensive explanation suitable for all levels of mathematical understanding. We'll also explore the exception to this rule and address common misconceptions. This will ensure a complete understanding of this fundamental concept in mathematics.
Understanding Exponents: A Foundation
Before tackling the central question, let's establish a firm understanding of exponents. An exponent, also known as a power or index, indicates how many times a number (the base) is multiplied by itself. For example:
- 5² (5 to the power of 2) = 5 × 5 = 25
- 5³ (5 to the power of 3) = 5 × 5 × 5 = 125
- 5⁴ (5 to the power of 4) = 5 × 5 × 5 × 5 = 625
Notice a pattern? As the exponent increases by one, we multiply the result by the base again. This consistent pattern is key to understanding what happens when the exponent becomes zero.
Method 1: The Pattern Approach
Let's examine the pattern of powers of 5 in descending order:
- 5⁴ = 625
- 5³ = 125
- 5² = 25
- 5¹ = 5
What happens next? To maintain the pattern, we divide the previous result by the base (5).
- 5⁰ = 5¹ / 5 = 5 / 5 = 1
This simple pattern demonstrates that 5 to the power of 0 logically equals 1. This pattern holds true for any non-zero base.
Method 2: The Algebraic Approach
Another way to understand this is through algebraic manipulation. Consider the following equation:
xⁿ / xᵐ = xⁿ⁻ᵐ
This is a fundamental rule of exponents. Now, let's substitute n = m:
xⁿ / xⁿ = xⁿ⁻ⁿ = x⁰
Since any number divided by itself equals 1 (except for zero, which we will address later), we have:
xⁿ / xⁿ = 1
Therefore, x⁰ = 1, which applies to any non-zero value of x. This proves algebraically why 5⁰ = 1.
Method 3: The Empty Product Approach
In mathematics, the empty product is a concept that helps explain this. Think of exponentiation as repeated multiplication. For instance:
5³ = 5 × 5 × 5
This represents three factors of 5. Similarly:
5² = 5 × 5 (two factors)
5¹ = 5 (one factor)
Following this logic, 5⁰ represents zero factors of 5. The empty product – multiplying nothing – is defined as 1. This is analogous to the additive identity of zero where adding nothing doesn't change the value. Thus, 5⁰ = 1.
Method 4: The Identity Element Approach
Consider the identity element for multiplication, which is 1. Any number multiplied by 1 remains unchanged. This property is crucial in understanding exponents. Let's observe the following:
x¹ = x (x multiplied by 1 is x) x² = x * x (x multiplied by x is x²) x³ = x * x * x (x multiplied by x multiplied by x is x³)
If we continue this pattern in reverse, we maintain consistency by dividing by x:
x¹ = x x⁰ = x¹ / x = x / x = 1
Therefore, the exponent of 0 maintains the multiplicative identity, resulting in 1.
Why is 0⁰ Undefined? The Exception to the Rule
While any non-zero number raised to the power of zero equals 1, the case of 0⁰ is undefined. This is because two conflicting patterns emerge:
-
Pattern 1: x⁰ = 1 for all x ≠ 0: As we've seen, this is consistent with the rules of exponents and the concept of the empty product.
-
Pattern 2: 0ˣ = 0 for all x > 0: Any positive exponent applied to zero results in zero.
These conflicting patterns create a conflict that mathematicians have not resolved. Attempting to define 0⁰ leads to inconsistencies and contradictions within mathematical systems. Hence, it remains undefined.
Common Misconceptions and Clarifications
Several common misconceptions surround 5⁰ (and x⁰ in general):
-
Mistaking it for zero: This is a common error. Remember the patterns and the algebraic explanations outlined above; it’s not zero.
-
Confusing it with negative exponents: Negative exponents denote reciprocals. 5⁻¹ = 1/5, not 0. These are distinct concepts.
-
Assuming it's only true for base 5: The principle holds for any non-zero base. It's a fundamental property of exponents.
Applications in Real World and Advanced Mathematics
The concept of 5⁰ (and x⁰) isn't just a theoretical curiosity. It has practical applications across various fields:
-
Combinatorics and Probability: Calculations involving combinations and permutations often utilize exponents, including the case of zero.
-
Calculus and Limits: Understanding the behavior of functions as exponents approach zero is crucial in calculus.
-
Computer Science: Exponentiation is fundamental in many algorithms and data structures.
-
Financial Mathematics: Compound interest calculations rely on exponential growth, involving scenarios where the time period (exponent) might be zero.
Conclusion: A Comprehensive Understanding
The seemingly simple question "What is 5 to the power of 0?" opens a doorway to a richer understanding of fundamental mathematical concepts. By exploring various approaches – patterns, algebraic manipulation, empty product, and identity element – we have established that 5⁰ = 1. This isn't a random assignment but a logical consequence of consistent mathematical rules. Understanding this principle is fundamental for success in higher-level mathematics and its applications in various fields. Remember the exception of 0⁰, which remains undefined due to conflicting mathematical patterns. This comprehensive explanation provides a solid foundation for further exploration of the fascinating world of exponents.
Latest Posts
Latest Posts
-
What Does With A Line Under It Mean
Jul 28, 2025
-
How Many Ounces Are In 350 Ml
Jul 28, 2025
-
How Many Potato Chips In One Ounce
Jul 28, 2025
-
36 Years Ago What Year Was It
Jul 28, 2025
-
What Does Wire In The Blood Mean
Jul 28, 2025
Related Post
Thank you for visiting our website which covers about What Is 5 To The Power Of 0 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.