What Is 6.25 As A Fraction
Kalali
Apr 22, 2025 · 5 min read
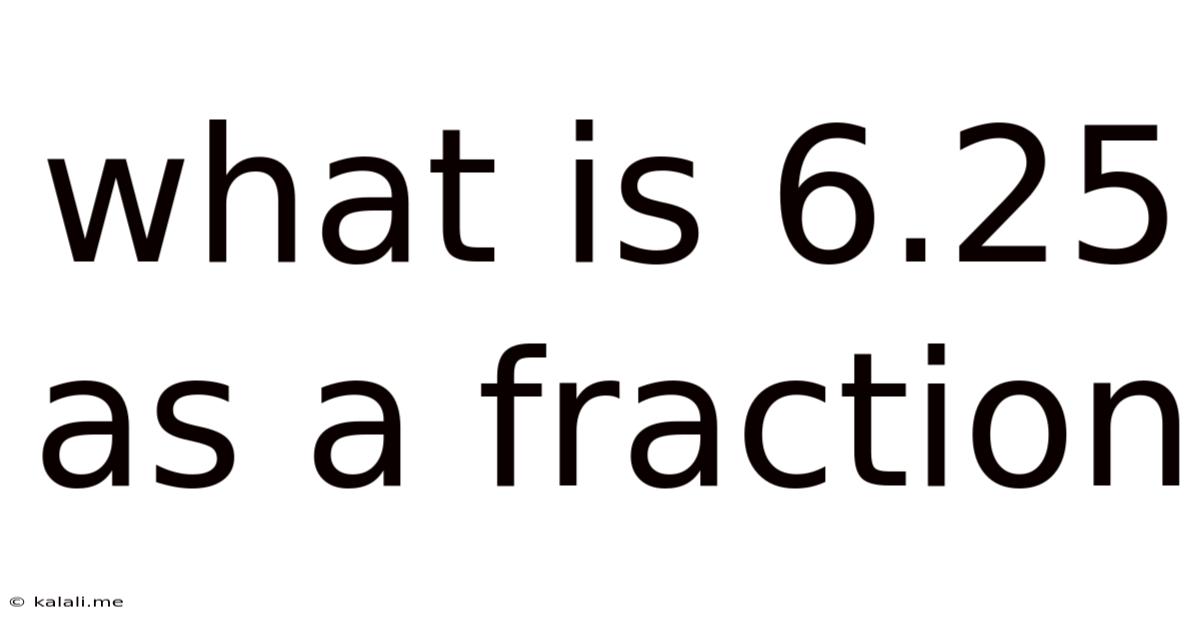
Table of Contents
What is 6.25 as a Fraction? A Comprehensive Guide
This article delves into the conversion of the decimal number 6.25 into its fractional equivalent. We'll explore different methods, explain the underlying concepts, and provide a thorough understanding of how to approach similar decimal-to-fraction conversions. Understanding this seemingly simple conversion is crucial for various mathematical applications, from basic arithmetic to more advanced calculations. This guide will help you master this essential skill.
Meta Description: Learn how to convert the decimal 6.25 into a fraction. This comprehensive guide explores multiple methods, explains the underlying concepts, and provides practical examples to help you master decimal-to-fraction conversions.
Understanding Decimal Numbers and Fractions
Before diving into the conversion, let's clarify the fundamental concepts of decimal numbers and fractions.
-
Decimal Numbers: Decimal numbers use a base-10 system, where each digit represents a power of 10. The digits to the left of the decimal point represent whole numbers, while the digits to the right represent fractions of a whole. For example, in 6.25, the '6' represents 6 whole units, the '2' represents 2 tenths (2/10), and the '5' represents 5 hundredths (5/100).
-
Fractions: Fractions represent parts of a whole. They consist of a numerator (the top number) and a denominator (the bottom number). The numerator indicates the number of parts, while the denominator indicates the total number of equal parts the whole is divided into. For example, 1/2 represents one out of two equal parts, or one-half.
Method 1: Using the Place Value System
This method directly utilizes the place value of each digit in the decimal number. Since 6.25 has two digits after the decimal point (hundredths place), we can express it as a fraction with a denominator of 100.
-
Write the decimal as a fraction with a denominator of 100: 6.25 can be written as 625/100. This is because the '2' is in the tenths place and the '5' is in the hundredths place. Therefore, we have 25 hundredths, added to the 6 whole units.
-
Simplify the fraction: We now simplify the fraction 625/100 by finding the greatest common divisor (GCD) of the numerator and the denominator. The GCD of 625 and 100 is 25. Dividing both the numerator and the denominator by 25, we get:
625 ÷ 25 = 25 100 ÷ 25 = 4
Therefore, 6.25 as a fraction is 25/4.
Method 2: Converting the Decimal Part Separately
This method involves separating the whole number part from the decimal part and converting the decimal part into a fraction before combining them.
-
Separate the whole number and the decimal part: Separate 6.25 into 6 (whole number) and 0.25 (decimal part).
-
Convert the decimal part to a fraction: 0.25 means 25 hundredths, which can be written as 25/100. Simplify this fraction by dividing both numerator and denominator by their GCD (25):
25 ÷ 25 = 1 100 ÷ 25 = 4
So, 0.25 as a fraction is 1/4.
-
Combine the whole number and the fractional part: Add the whole number (6) to the simplified fraction (1/4):
6 + 1/4 = 6 1/4 or 25/4 (converting the mixed number to an improper fraction)
Therefore, 6.25 as a fraction is 25/4 or 6 1/4.
Method 3: Using the Concept of Equivalent Fractions
This method involves finding an equivalent fraction with a denominator that is a power of 10. While less direct for this particular example, it's a useful technique for more complex decimal conversions.
Since 6.25 has two decimal places, we could initially represent it as 625/100. Then, by recognizing that both the numerator and the denominator are divisible by 25, we could simplify it directly to 25/4.
This method highlights that multiple equivalent fractions can represent the same value. The simplest form, however, is usually preferred for clarity.
Understanding Improper Fractions and Mixed Numbers
The result of our conversions, 25/4, is an improper fraction because the numerator (25) is larger than the denominator (4). We can also express this as a mixed number, which combines a whole number and a proper fraction: 6 1/4. Both represent the same value.
- Improper Fraction: A fraction where the numerator is greater than or equal to the denominator.
- Mixed Number: A number that combines a whole number and a proper fraction.
Practical Applications and Further Exploration
The ability to convert decimals to fractions is essential in various fields:
- Baking and Cooking: Recipes often require fractional measurements, and understanding decimal-to-fraction conversions helps in accurate ingredient measurements.
- Engineering and Construction: Precision is crucial in these fields, and converting between decimals and fractions ensures accurate calculations and measurements.
- Finance and Accounting: Working with percentages and proportions frequently involves converting between decimals and fractions.
- Mathematics: Many mathematical problems require working with fractions, and the ability to convert decimals to fractions is a fundamental skill.
Beyond the simple conversion of 6.25, the methods described here can be applied to any decimal number. The key is to understand the place value system, the concept of greatest common divisor (GCD), and the relationship between decimals and fractions. Practice with various decimal numbers will solidify your understanding and make you proficient in these conversions. Remember to always simplify your fractions to their lowest terms for the most concise representation.
Troubleshooting Common Mistakes
-
Incorrect Place Value: Ensure you correctly identify the place value of each digit after the decimal point when converting to a fraction. A common error is misinterpreting tenths, hundredths, thousandths, etc.
-
Incorrect Simplification: Always simplify your fractions to their lowest terms by dividing both the numerator and denominator by their greatest common divisor (GCD). Failure to simplify leads to an inaccurate or less elegant representation.
-
Mixing Improper and Mixed Numbers: While both are valid representations, ensure you understand the difference and use the appropriate form based on the context of the problem.
-
Errors in Arithmetic: Double-check your calculations at each step to minimize errors in addition, subtraction, multiplication, and division.
This comprehensive guide provides a solid foundation for converting decimal numbers to fractions. By understanding the underlying principles and practicing the different methods, you can confidently tackle similar conversions and apply this crucial skill in various contexts. Remember to always simplify your fractions to their lowest terms for the clearest and most accurate representation.
Latest Posts
Latest Posts
-
What Is 147 Centimeters In Feet
Apr 22, 2025
-
Convert 51 Degrees Fahrenheit To Celsius
Apr 22, 2025
-
What Is Lcm Of 9 And 12
Apr 22, 2025
-
48 Feet Is How Many Inches
Apr 22, 2025
-
108 Minutes Is How Many Hours
Apr 22, 2025
Related Post
Thank you for visiting our website which covers about What Is 6.25 As A Fraction . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.