What Is 6/5 As A Mixed Number
Kalali
Apr 24, 2025 · 5 min read
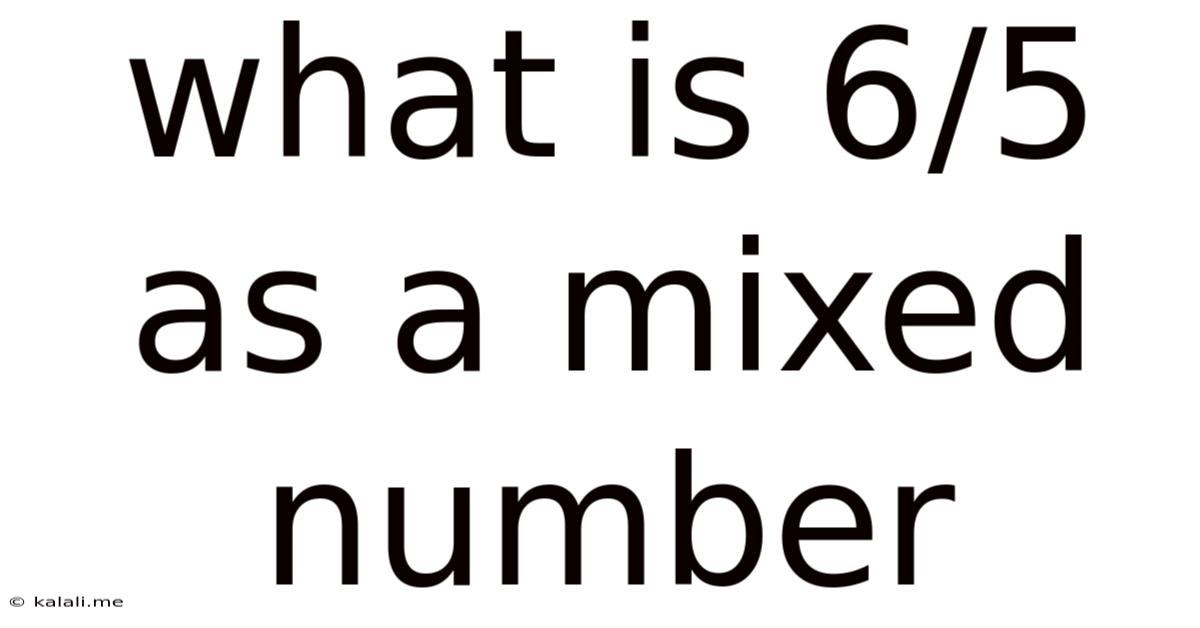
Table of Contents
What is 6/5 as a Mixed Number? A Deep Dive into Fraction Conversion
This article will thoroughly explore the conversion of the improper fraction 6/5 into a mixed number. We'll cover the fundamental concepts, step-by-step instructions, real-world applications, and even delve into the broader mathematical context of fractions and mixed numbers. Understanding this seemingly simple conversion is crucial for a strong foundation in arithmetic and algebra.
Meta Description: Learn how to convert the improper fraction 6/5 into a mixed number. This comprehensive guide explains the process step-by-step, provides real-world examples, and explores the underlying mathematical concepts. Master fraction conversion today!
Understanding Fractions and Mixed Numbers
Before diving into the conversion, let's clarify the definitions of improper fractions and mixed numbers.
-
Improper Fraction: An improper fraction is a fraction where the numerator (the top number) is greater than or equal to the denominator (the bottom number). For example, 6/5, 7/3, and 11/4 are all improper fractions. They represent a value greater than or equal to one.
-
Mixed Number: A mixed number combines a whole number and a proper fraction. A proper fraction is a fraction where the numerator is smaller than the denominator (e.g., 1/2, 3/4, 2/5). Mixed numbers provide a more intuitive way to represent values greater than one. For example, 1 1/2, 2 2/3, and 3 1/4 are all mixed numbers.
Converting 6/5 to a Mixed Number: A Step-by-Step Guide
The conversion of 6/5 to a mixed number involves a simple division process. Here's how to do it:
-
Divide the numerator by the denominator: Divide 6 (the numerator) by 5 (the denominator). 6 ÷ 5 = 1 with a remainder of 1.
-
The whole number part: The quotient (the result of the division) becomes the whole number part of the mixed number. In this case, the quotient is 1.
-
The fractional part: The remainder (the number left over after the division) becomes the numerator of the fractional part. The denominator remains the same as the original fraction. So, the remainder is 1, and the denominator remains 5. This gives us the fraction 1/5.
-
Combine the whole number and the fraction: Combine the whole number from step 2 and the fraction from step 3 to form the mixed number. Therefore, 6/5 as a mixed number is 1 1/5.
Visualizing the Conversion
Imagine you have six fifths of a pizza. You can easily separate this into one whole pizza (5/5) and one-fifth of a pizza (1/5) left over. This visually represents the conversion of 6/5 to 1 1/5. This visual representation helps solidify the understanding of the conversion process.
Real-World Applications of Fraction Conversion
The ability to convert between improper fractions and mixed numbers is crucial in various real-world scenarios:
-
Cooking and Baking: Recipes often require fractional measurements. Converting improper fractions to mixed numbers makes it easier to understand and measure ingredients. For instance, a recipe might call for 7/4 cups of flour, which is easier to measure as 1 3/4 cups.
-
Construction and Engineering: Precise measurements are essential in construction and engineering. Converting fractions is necessary for accurate calculations and measurements.
-
Finance and Accounting: Fractions are commonly used in financial calculations, such as calculating interest rates or proportions of investments. Converting improper fractions to mixed numbers can improve clarity and understanding.
-
Data Analysis: In data analysis, you might encounter fractions representing proportions or percentages. Converting them to mixed numbers can help to visualize the data more easily.
Further Exploration: Working with More Complex Fractions
Let's extend our understanding by working through a few more examples:
-
Convert 11/3 to a mixed number:
- 11 ÷ 3 = 3 with a remainder of 2.
- Whole number: 3
- Fraction: 2/3
- Mixed number: 3 2/3
-
Convert 17/5 to a mixed number:
- 17 ÷ 5 = 3 with a remainder of 2.
- Whole number: 3
- Fraction: 2/5
- Mixed number: 3 2/5
-
Convert 25/4 to a mixed number:
- 25 ÷ 4 = 6 with a remainder of 1.
- Whole number: 6
- Fraction: 1/4
- Mixed number: 6 1/4
These examples demonstrate the consistent application of the division method for converting improper fractions to mixed numbers. The process remains the same regardless of the specific numbers involved.
Converting Mixed Numbers back to Improper Fractions
It's also essential to understand the reverse process: converting a mixed number back into an improper fraction. This involves the following steps:
-
Multiply the whole number by the denominator: Multiply the whole number by the denominator of the fraction.
-
Add the numerator: Add the numerator of the fraction to the result from step 1.
-
The new numerator: This sum becomes the new numerator of the improper fraction.
-
The denominator stays the same: The denominator remains unchanged.
Let's convert the mixed number 1 1/5 back into an improper fraction:
- 1 (whole number) × 5 (denominator) = 5
- 5 + 1 (numerator) = 6
- New numerator: 6
- Denominator: 5
- Improper fraction: 6/5
This demonstrates the inverse relationship between improper fractions and mixed numbers. You can always convert between the two forms using these methods.
The Importance of Understanding Fraction Conversion in Higher Mathematics
The ability to convert between fractions and mixed numbers is fundamental to success in more advanced mathematical concepts. This skill is crucial for:
-
Algebra: Solving equations and simplifying expressions often involves manipulating fractions.
-
Calculus: Calculus extensively utilizes fractions and requires a solid understanding of their manipulation.
-
Geometry: Geometric problems often involve fractional calculations and measurements.
-
Statistics: Statistical analysis relies heavily on working with fractions and proportions.
Mastering the seemingly simple conversion of 6/5 to 1 1/5 lays a solid groundwork for tackling more complex mathematical problems later on. The ability to confidently convert between improper fractions and mixed numbers is a testament to a strong foundational understanding of arithmetic. This skill enables greater fluency and efficiency in mathematical problem-solving, across various disciplines and applications. Continue practicing these conversions to further solidify your understanding and prepare for more advanced mathematical challenges.
Latest Posts
Latest Posts
-
What Is 6875 As A Fraction
Apr 25, 2025
-
How Many Seconds Is 6 Minutes
Apr 25, 2025
-
How Many Minutes Is 16 Hours
Apr 25, 2025
-
Convert 38 Degrees Celsius To Fahrenheit
Apr 25, 2025
-
What Percent Is 20 Out Of 60
Apr 25, 2025
Related Post
Thank you for visiting our website which covers about What Is 6/5 As A Mixed Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.