What Is 6 As A Percentage Of 10
Kalali
Apr 09, 2025 · 4 min read
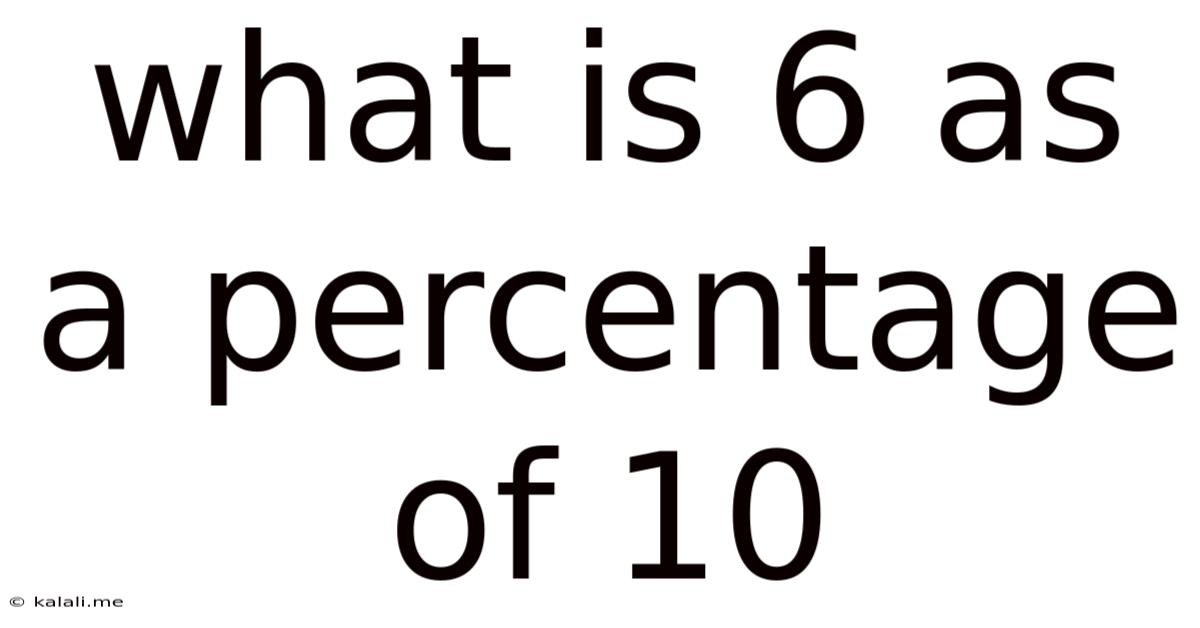
Table of Contents
What is 6 as a Percentage of 10? A Deep Dive into Percentage Calculations
This seemingly simple question – "What is 6 as a percentage of 10?" – opens the door to a broader understanding of percentages, their applications, and how to effectively calculate them. While the answer itself is straightforward (60%), the process and underlying concepts are crucial for numerous applications in daily life, academics, and professional fields. This article will not only provide the answer but delve into the methodology, explore practical examples, and discuss the importance of percentage calculations.
Understanding Percentages: The Foundation
A percentage is a way of expressing a number as a fraction of 100. The term "percent" literally means "out of one hundred" (per centum in Latin). Therefore, 60% means 60 out of 100, or 60/100. This fundamental understanding is key to solving percentage problems. Understanding fractions and decimals is equally crucial, as percentages are closely related to both. In fact, percentages are simply another way to represent fractional or decimal values.
Calculating 6 as a Percentage of 10: The Simple Method
The most straightforward approach involves a simple formula:
(Part / Whole) x 100 = Percentage
In this case:
- Part: 6 (the number we want to express as a percentage)
- Whole: 10 (the total number)
Substituting these values into the formula:
(6 / 10) x 100 = 60%
Therefore, 6 is 60% of 10.
Expanding the Understanding: Different Approaches
While the above method is efficient, understanding alternative approaches strengthens conceptual understanding. Let's explore two additional methods:
Method 2: Using Decimal Equivalents
We can first convert the fraction 6/10 into a decimal:
6 / 10 = 0.6
Then, to convert the decimal to a percentage, simply multiply by 100:
0.6 x 100 = 60%
Method 3: Proportions
This method involves setting up a proportion:
6/10 = x/100
To solve for x (the percentage), cross-multiply:
10x = 600
x = 600 / 10 = 60%
Practical Applications of Percentage Calculations
Percentage calculations are ubiquitous in various aspects of life. Here are some examples:
-
Sales and Discounts: Retailers frequently advertise discounts as percentages (e.g., "20% off"). Understanding percentages allows consumers to quickly calculate the final price after a discount.
-
Finance and Investments: Interest rates on loans and investments are expressed as percentages. Calculating interest earned or owed requires an understanding of percentage calculations. Compound interest calculations, in particular, rely heavily on percentages.
-
Statistics and Data Analysis: Percentages are fundamental to interpreting statistical data. For example, expressing survey results, market share, or population demographics often involves percentages. Understanding percentage change and percentage point difference are crucial skills here.
-
Science and Engineering: Many scientific and engineering calculations involve percentages, such as calculating efficiency, error margins, and concentrations.
-
Everyday Life: Calculating tips at restaurants, determining tax amounts, and understanding nutritional information on food labels all involve percentage calculations. Even something as simple as figuring out your grade in a class often relies on calculating percentages.
Beyond the Basics: Advanced Percentage Calculations
While finding 6 as a percentage of 10 is relatively simple, more complex percentage problems require a deeper understanding. Let's explore some common scenarios:
- Finding the Percentage Increase or Decrease: This involves calculating the percentage change between two values. The formula is:
[(New Value - Old Value) / Old Value] x 100 = Percentage Change
For example, if a product's price increased from $10 to $12, the percentage increase is:
[(12 - 10) / 10] x 100 = 20%
- Finding a Percentage of a Number: This involves calculating a specific percentage of a given value. For example, finding 15% of 200:
0.15 x 200 = 30
- Finding the Original Value After a Percentage Change: This involves working backward from a final value to find the original value before a percentage increase or decrease. This often requires using algebraic manipulation to solve for the unknown original value.
Troubleshooting Common Errors in Percentage Calculations
Even with a solid understanding of the fundamentals, common errors can occur. Here are some frequent pitfalls:
-
Incorrect Order of Operations: Ensure that you follow the order of operations (PEMDAS/BODMAS) correctly, especially when dealing with more complex calculations.
-
Confusing Percentage Points and Percentages: A change of 10 percentage points is different from a 10% increase.
-
Misinterpreting the "Whole": Always correctly identify the "whole" or the total amount when calculating percentages. This is crucial for accurate results.
-
Rounding Errors: Be mindful of rounding errors, especially when dealing with multiple calculations. Avoid premature rounding to maintain accuracy.
Conclusion: Mastering the Power of Percentages
Understanding how to calculate percentages, even something as basic as "What is 6 as a percentage of 10?", is a fundamental skill with far-reaching applications. From managing personal finances to analyzing complex data, the ability to confidently work with percentages is invaluable. This article has provided not only the answer to the initial question but has also explored various methods for calculating percentages, highlighted practical applications, and addressed common errors. By mastering these concepts, you equip yourself with a powerful tool for navigating various aspects of life and work. The ability to quickly and accurately perform percentage calculations is a valuable skill that will serve you well in many contexts. Remember that consistent practice and a solid understanding of the underlying principles are key to achieving mastery.
Latest Posts
Latest Posts
-
How To Find The Lcd Of A Rational Equation
Apr 17, 2025
-
What Is The Fraction For 4 5
Apr 17, 2025
-
How Many Valence Electrons Do Alkaline Earth Metals Have
Apr 17, 2025
-
How Much Is 18cm In Inches
Apr 17, 2025
-
What Is 17 Percent Of 20
Apr 17, 2025
Related Post
Thank you for visiting our website which covers about What Is 6 As A Percentage Of 10 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.