What Is 6 To The Power Of 3
Kalali
Apr 01, 2025 · 5 min read
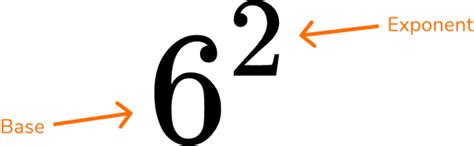
Table of Contents
What is 6 to the Power of 3? A Deep Dive into Exponents and Their Applications
The seemingly simple question, "What is 6 to the power of 3?" opens a door to a vast world of mathematical concepts, practical applications, and intriguing explorations. At its core, it's a basic exponentiation problem, but understanding its implications reveals much about the elegance and power of mathematics. This article will not only answer the initial question but will delve deeper into the meaning of exponents, their uses in various fields, and related mathematical concepts.
Understanding Exponents: The Basics
Before tackling 6 to the power of 3, let's establish a firm understanding of exponents. An exponent, also known as a power or index, indicates how many times a number (the base) is multiplied by itself. The expression bⁿ represents b multiplied by itself n times. Here, b is the base, and n is the exponent.
For example:
- 2³ = 2 x 2 x 2 = 8 (2 is the base, 3 is the exponent)
- 5² = 5 x 5 = 25 (5 is the base, 2 is the exponent)
- 10¹ = 10 (10 is the base, 1 is the exponent; any number raised to the power of 1 is itself)
- 7⁰ = 1 (Any non-zero number raised to the power of 0 is 1)
Calculating 6 to the Power of 3
Now, let's address the central question: What is 6 to the power of 3 (6³)?
This means multiplying 6 by itself three times:
6³ = 6 x 6 x 6 = 216
Therefore, 6 to the power of 3 equals 216. This simple calculation forms the foundation for numerous more complex mathematical operations and applications.
Beyond the Calculation: Exploring the Applications of Exponents
The concept of exponents extends far beyond simple calculations. They are fundamental to various areas, including:
1. Science and Engineering
- Compound Interest: Exponents are crucial in calculating compound interest. The formula A = P(1 + r/n)^(nt) uses exponents to determine the future value (A) of an investment based on the principal amount (P), interest rate (r), number of times interest is compounded per year (n), and the number of years (t). Understanding exponential growth is vital for financial planning.
- Exponential Decay: Many natural processes, such as radioactive decay, follow an exponential decay pattern. The formula for this often involves negative exponents, describing how a quantity decreases over time. This is crucial in fields like nuclear physics and medicine (radioactive isotopes in medical treatments).
- Growth of Populations: Population growth, whether of bacteria, animals, or even humans, can often be modeled using exponential functions. Understanding exponential growth helps in predicting future population sizes and managing resources.
- Physics: Exponents are fundamental in numerous physical laws and formulas. For instance, the inverse square law, which describes how the intensity of light or gravity decreases with distance, involves exponents.
2. Computer Science
- Big O Notation: In computer science, Big O notation uses exponents to describe the efficiency of algorithms. For example, an algorithm with O(n²) time complexity means its execution time increases proportionally to the square of the input size (n). This helps in choosing the most efficient algorithms for a given problem.
- Binary Numbers: The binary number system, the foundation of computer programming, uses powers of 2. Each digit represents a power of 2, contributing to the overall value of the binary number. Understanding exponents is crucial for working with binary data.
- Data Structures: The performance of many data structures, such as trees and graphs, is often analyzed using exponential functions to determine the time or space complexity of operations.
3. Mathematics
- Polynomial Equations: Exponents are essential elements in polynomial equations, which are used to model many real-world phenomena and solve various mathematical problems.
- Calculus: Derivatives and integrals, fundamental concepts in calculus, involve the use of exponents. Understanding exponents is essential for mastering calculus.
- Algebra: Exponents are fundamental tools in algebraic manipulations and equation solving.
4. Other Fields
- Finance: Apart from compound interest, exponents appear in options pricing models, determining the value of financial derivatives.
- Statistics: Exponents are crucial in various statistical distributions, like the normal distribution.
- Economics: Exponential functions are used to model economic growth, decay, and various other economic phenomena.
Exploring Related Mathematical Concepts
Understanding 6 to the power of 3 opens doors to exploring related concepts, including:
1. Roots and Radicals
The inverse operation of exponentiation is finding the root of a number. For example, the cube root of 216 (∛216) is 6, as 6 x 6 x 6 = 216. Understanding roots and radicals allows us to solve for the base when the exponent and result are known.
2. Logarithms
Logarithms are another related concept. The logarithm of a number to a given base is the exponent to which the base must be raised to produce that number. For instance, the logarithm base 6 of 216 (log₆216) is 3. Logarithms have many applications, particularly in solving equations involving exponents.
3. Scientific Notation
Scientific notation utilizes exponents to represent very large or very small numbers concisely. For example, the speed of light (approximately 300,000,000 meters per second) can be expressed as 3 x 10⁸ m/s. This simplifies calculations and makes working with extremely large or small numbers much more manageable.
Conclusion: The Significance of a Simple Calculation
While the calculation of 6 to the power of 3 might seem trivial at first glance, it serves as a gateway to a world of complex and powerful mathematical concepts. Its applications span numerous fields, highlighting the importance of understanding exponents in various contexts. From finance and engineering to computer science and pure mathematics, the ability to work with exponents is a fundamental skill with far-reaching consequences. This exploration not only provides an answer to the initial question but emphasizes the broader significance of a seemingly simple mathematical operation within the wider landscape of mathematical principles and their practical applications. Mastering this fundamental concept opens doors to deeper understanding and problem-solving capabilities across various disciplines.
Latest Posts
Latest Posts
-
How Many Centimeters Is 23 Inches
Apr 02, 2025
-
How Many Gallons Is 10 Cups
Apr 02, 2025
-
What Is 62 Degrees Celsius In Fahrenheit
Apr 02, 2025
-
Is Usa In The Northern Hemisphere
Apr 02, 2025
-
How Many Glasses Is 32 Oz Of Water
Apr 02, 2025
Related Post
Thank you for visiting our website which covers about What Is 6 To The Power Of 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
