What Is 60 Off Of 25
Kalali
Apr 25, 2025 · 5 min read
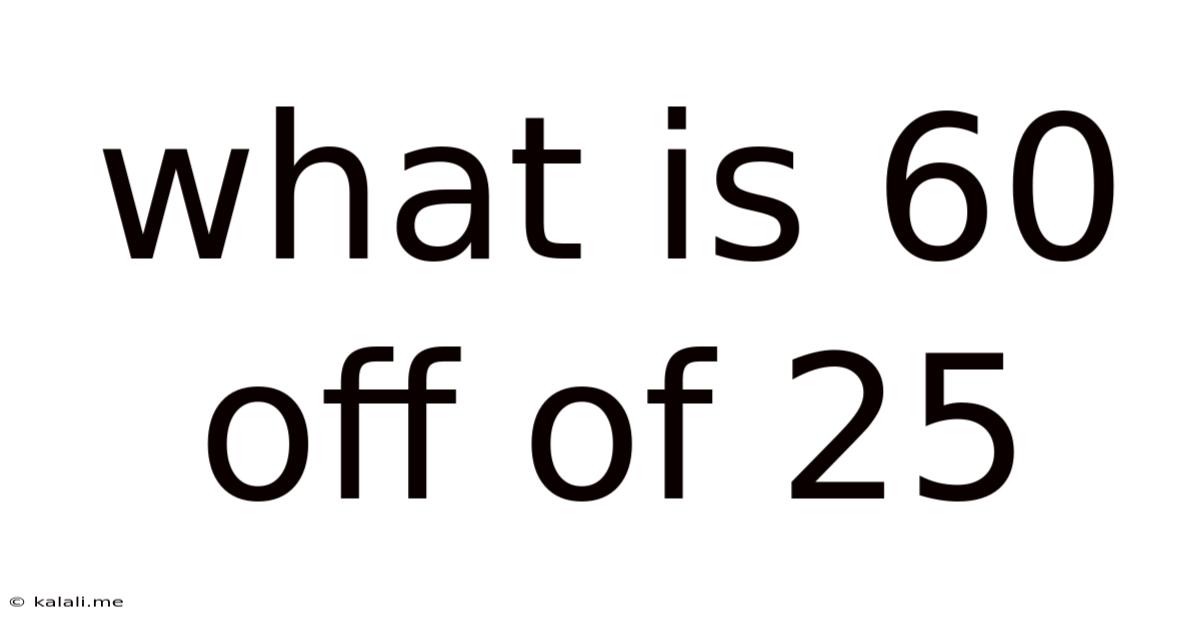
Table of Contents
What is 60% Off of 25? A Comprehensive Guide to Percentage Calculations
This seemingly simple question, "What is 60% off of 25?", opens the door to a broader understanding of percentage calculations, a crucial skill in various aspects of life, from shopping and budgeting to business and finance. This article will not only answer the initial question but also delve into the methods, applications, and variations of percentage calculations, providing you with a comprehensive understanding of this essential mathematical concept. Understanding percentages helps you make informed decisions, whether you're comparing deals, calculating discounts, or analyzing financial data.
Meta Description: Learn how to calculate 60% off of 25 and master percentage calculations. This comprehensive guide covers various methods, real-world applications, and practical tips for accurate and efficient percentage computations.
Understanding Percentages: The Basics
A percentage is a fraction or ratio expressed as a number out of 100. The symbol "%" represents "percent" or "out of 100". So, 60% means 60 out of 100, or 60/100, which simplifies to 3/5. Understanding this fundamental concept is vital before tackling more complex percentage problems. We use percentages to represent proportions, changes, and comparisons across various fields.
Method 1: Calculating 60% of 25 Directly
The most straightforward way to find 60% off of 25 is to first calculate 60% of 25 and then subtract that amount from 25.
- Find 60% of 25: To do this, we convert the percentage to a decimal by dividing by 100: 60% = 60/100 = 0.60.
- Multiply by the original value: Multiply 0.60 by 25: 0.60 * 25 = 15. This means 60% of 25 is 15.
- Subtract from the original value: Subtract the result (15) from the original value (25): 25 - 15 = 10.
Therefore, 60% off of 25 is $\boxed{10}$.
Method 2: Calculating the Remaining Percentage
An alternative approach is to calculate the remaining percentage (40%) and apply that to the original value. Since 60% is being discounted, 40% (100% - 60%) remains.
- Calculate the remaining percentage: 100% - 60% = 40%.
- Convert to decimal: 40% = 40/100 = 0.40.
- Multiply by the original value: 0.40 * 25 = 10.
This method also yields the same result: $\boxed{10}$. This method can be particularly useful when dealing with multiple discounts or complex scenarios.
Real-World Applications of Percentage Calculations
Understanding percentage calculations is essential in numerous real-world scenarios:
- Shopping and Sales: Calculating discounts, sales tax, and comparing prices are all reliant on percentage calculations. Whether it's a 20% off sale or a 15% discount for members, understanding percentages empowers you to make informed purchasing decisions and save money.
- Finance and Budgeting: Calculating interest rates, loan payments, and investment returns all involve percentages. Understanding these calculations helps in managing personal finances, investing wisely, and making sound financial decisions.
- Business and Economics: Analyzing market trends, calculating profit margins, and determining pricing strategies all rely heavily on percentage calculations. Businesses utilize percentages to track performance, assess risks, and make strategic decisions.
- Science and Data Analysis: Percentages are widely used to represent proportions, probabilities, and changes in data analysis across various fields, including science, healthcare, and social sciences. Understanding how percentages represent data is crucial for interpreting research findings and drawing accurate conclusions.
Variations and Advanced Percentage Problems
While the initial problem was straightforward, percentage calculations can become more complex. Let's explore some variations:
- Multiple Discounts: Imagine a situation where you have a 20% discount followed by an additional 10% discount. You cannot simply add the percentages (30%). Instead, you must apply each discount sequentially. First, calculate the price after the 20% discount, and then apply the 10% discount to the new price.
- Percentage Increase/Decrease: Understanding how to calculate percentage increases or decreases is crucial for tracking changes in values over time. For example, calculating the percentage increase in sales from one year to another, or the percentage decrease in unemployment rate.
- Finding the Original Value: Sometimes, you know the discounted price and the percentage discount and need to find the original value. This involves working backward using algebraic equations.
- Compound Interest: Compound interest involves earning interest on both the principal amount and accumulated interest. This calculation uses exponential growth, and understanding the underlying percentage calculations is essential for comprehending its effects over time.
Tips for Accurate Percentage Calculations
- Convert percentages to decimals: Always convert percentages to decimals (by dividing by 100) before performing calculations. This simplifies the process and reduces the chance of errors.
- Use a calculator: For complex calculations, utilize a calculator to ensure accuracy and save time.
- Check your work: After completing a calculation, review your work to ensure the result is logical and makes sense within the context of the problem.
- Practice regularly: The more you practice percentage calculations, the more comfortable and proficient you will become. Start with simple problems and gradually increase the complexity.
Conclusion: Mastering Percentage Calculations
This article has demonstrated various methods for calculating percentages, applied these methods to solve the problem "What is 60% off of 25?", and explored the wide-ranging applications of percentage calculations in everyday life and various professional fields. Mastering percentage calculations is not just about solving mathematical problems; it's about acquiring a critical skill that empowers you to make informed decisions, analyze data effectively, and navigate the complexities of the modern world. By understanding the fundamental concepts and practicing regularly, you can confidently tackle any percentage-related challenge that comes your way. From simple discounts to complex financial analyses, the ability to accurately calculate percentages is an invaluable asset. Remember to break down complex problems into smaller, manageable steps, and always double-check your work to ensure accuracy. The more you practice, the more intuitive and effortless percentage calculations will become.
Latest Posts
Latest Posts
-
Cuanto Es 83 Grados Fahrenheit En Centigrados
Apr 26, 2025
-
26 Oz Is How Many Ml
Apr 26, 2025
-
What Is 11 Out Of 16
Apr 26, 2025
-
One Percent Of A Million Dollars
Apr 26, 2025
-
How Much Is 240ml In Cups
Apr 26, 2025
Related Post
Thank you for visiting our website which covers about What Is 60 Off Of 25 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.