What Is 60 Percent Of 25
Kalali
Apr 17, 2025 · 5 min read
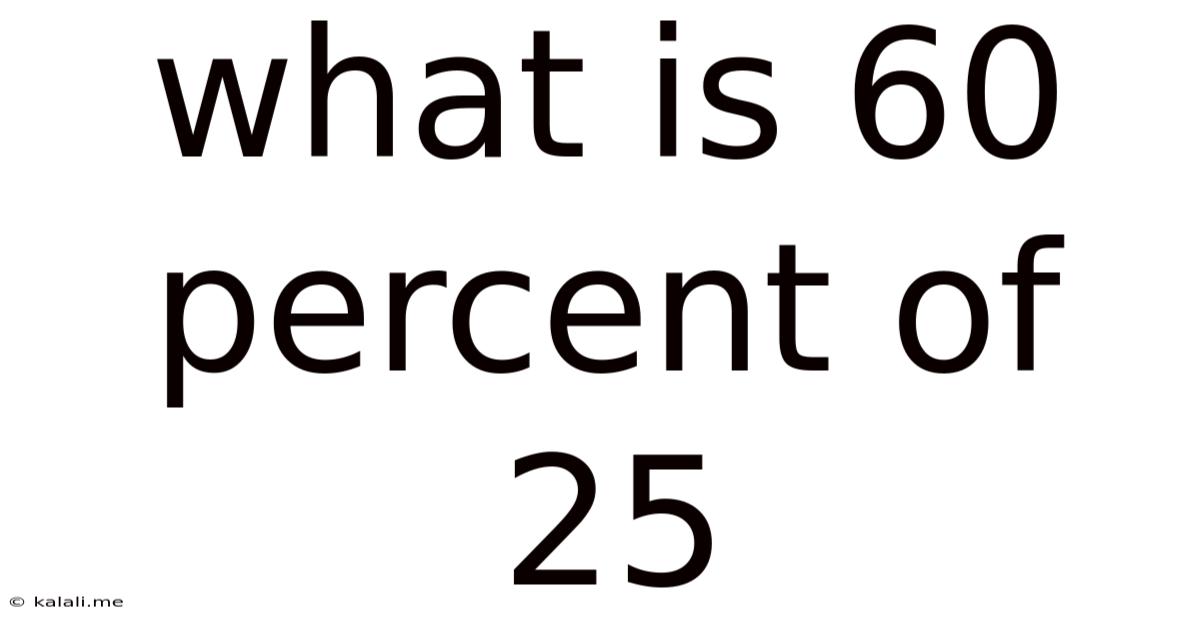
Table of Contents
What is 60 Percent of 25? A Deep Dive into Percentages and Their Applications
This seemingly simple question, "What is 60 percent of 25?", opens the door to a vast world of mathematical concepts and their practical applications. While the answer itself is easily calculable, understanding the underlying principles of percentages and how they're used in various fields is crucial. This article will not only provide the solution but also explore the broader context of percentage calculations, their importance in everyday life, and advanced techniques for handling more complex percentage problems.
Meta Description: Discover the answer to "What is 60 percent of 25?" and delve into the world of percentage calculations. This comprehensive guide explores various methods, applications, and practical examples of percentage problems, providing a solid understanding for both beginners and intermediate learners.
Understanding Percentages: A Foundation for Calculation
A percentage is a way of expressing a number as a fraction of 100. The word "percent" literally means "out of one hundred." Therefore, 60% is equivalent to 60/100, or 0.6 as a decimal. This fundamental understanding is key to solving any percentage problem. The basic formula for calculating a percentage of a number is:
(Percentage/100) * Number = Result
In our case:
(60/100) * 25 = 15
Therefore, 60 percent of 25 is $\boxed{15}$.
Multiple Methods for Calculating Percentages
While the above formula is the most straightforward, several other methods can be used to calculate percentages, each with its own advantages depending on the complexity of the problem and personal preference.
1. Using Decimal Equivalents:
As mentioned earlier, 60% is equivalent to 0.6. Multiplying 25 by 0.6 directly gives the answer: 25 * 0.6 = 15. This method is particularly efficient for simple calculations and is easily adaptable for use in spreadsheets or programming.
2. Using Fractions:
60% can also be expressed as the fraction 60/100, which simplifies to 3/5. Multiplying 25 by 3/5 gives: (3/5) * 25 = 15. This method is useful when dealing with fractions or when simplifying calculations mentally.
3. Using Proportions:
Percentage problems can be solved using proportions. We can set up a proportion as follows:
60/100 = x/25
Cross-multiplying and solving for x:
100x = 60 * 25 100x = 1500 x = 15
This method is particularly useful for understanding the relationship between the percentage, the whole, and the part.
4. Using a Calculator:
Most calculators have a percentage function (%) that simplifies the process. Simply enter 60%, then the multiplication symbol, then 25, and press equals. The calculator will automatically perform the calculation and display the result: 15. This is the most convenient method for quick calculations.
Practical Applications of Percentage Calculations
Percentages are ubiquitous in everyday life, appearing in various contexts, including:
-
Finance: Calculating interest rates, discounts, taxes, profits, and losses. Understanding percentages is fundamental for managing personal finances and making informed financial decisions. For example, calculating the interest earned on a savings account or the amount of tax owed on a purchase requires precise percentage calculations.
-
Retail: Determining discounts, sales tax, and markups. Stores frequently advertise sales using percentages, and understanding these percentages allows consumers to determine the actual savings. Similarly, businesses utilize percentage calculations to determine profit margins and pricing strategies.
-
Science: Representing data in graphs and charts, expressing experimental results, and calculating statistical measures. Percentages are a crucial tool for representing data concisely and effectively in various scientific fields.
-
Education: Grading systems, calculating averages, and assessing student performance. School grades are often expressed as percentages, providing a clear indication of student progress.
-
Statistics: Expressing probabilities, representing distributions, and analyzing data. Percentages are essential for interpreting and communicating statistical findings.
Advanced Percentage Problems and Techniques
While calculating 60% of 25 is relatively simple, more complex problems require a deeper understanding of percentage relationships. Consider these examples:
- Finding the percentage increase or decrease: If a price increases from $20 to $25, the percentage increase is calculated as follows:
((25-20)/20) * 100% = 25%
- Finding the original value after a percentage change: If a price is reduced by 20% to $20, the original price is calculated as follows:
$20 / (1 - 0.20) = $25
-
Calculating percentages with multiple changes: If a price increases by 10% and then decreases by 10%, the final price will not be the same as the original price. This is due to the fact that the second percentage change is applied to the new price, not the original price.
-
Solving percentage word problems: Word problems often require careful analysis to identify the relevant information and set up the correct equation.
Tips for Mastering Percentage Calculations
-
Practice regularly: The more you practice, the more comfortable you will become with percentage calculations.
-
Understand the underlying concepts: Focus on understanding the meaning of percentages and their relationship to fractions and decimals.
-
Use different methods: Experiment with various calculation methods to find the ones that work best for you.
-
Break down complex problems: Divide complex problems into smaller, more manageable steps.
-
Check your work: Always double-check your calculations to ensure accuracy.
Conclusion: Beyond the Simple Answer
The answer to "What is 60 percent of 25?" is 15. However, the true value of this seemingly simple question lies in its ability to illuminate the broader world of percentages and their applications. By understanding the fundamental principles of percentage calculations and mastering various solution methods, individuals can confidently tackle more complex percentage problems encountered in everyday life, academic pursuits, and professional fields. The ability to work with percentages is a vital skill that extends far beyond the confines of a simple mathematical equation.
Latest Posts
Latest Posts
-
What Is 98 Inches In Feet
Apr 19, 2025
-
How Many Cups Are In 20oz
Apr 19, 2025
-
How Many Diagonals Has A Hexagon
Apr 19, 2025
-
9 As A Percentage Of 25
Apr 19, 2025
-
What Is 1 12 In A Decimal
Apr 19, 2025
Related Post
Thank you for visiting our website which covers about What Is 60 Percent Of 25 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.