What Is 60 Percent Of 40
Kalali
Apr 09, 2025 · 6 min read
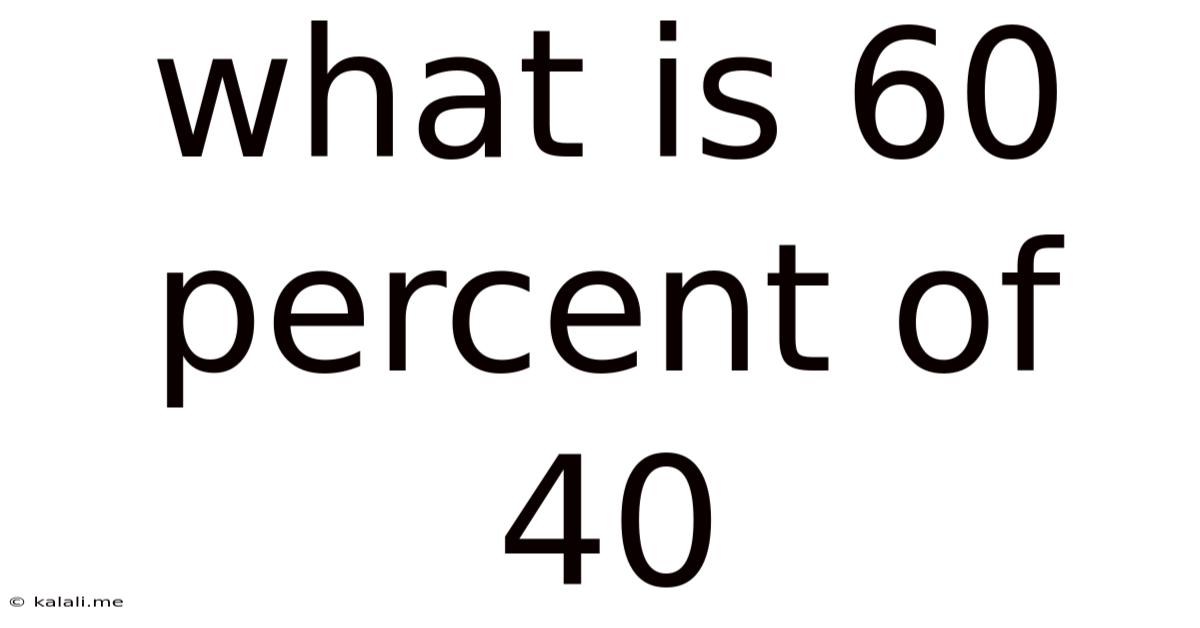
Table of Contents
What is 60 Percent of 40? A Deep Dive into Percentages and Their Applications
This seemingly simple question, "What is 60 percent of 40?", opens a door to a vast world of mathematical concepts and practical applications. While the answer itself is straightforward, understanding the underlying principles of percentages and their diverse uses is crucial for navigating various aspects of life, from everyday finances to complex scientific calculations. This article will not only answer the initial question but also explore the broader context of percentages, providing you with a comprehensive understanding of this fundamental mathematical tool.
Meta Description: Learn how to calculate 60% of 40 and delve into the world of percentages. This comprehensive guide explains percentage calculations, their real-world applications, and provides valuable tips for mastering this essential mathematical skill.
Calculating 60% of 40: The Basic Approach
The most straightforward method to calculate 60% of 40 involves converting the percentage into a decimal and then multiplying it by the number. Sixty percent can be written as 0.60 (or simply 0.6). Therefore, the calculation is as follows:
0.6 * 40 = 24
Therefore, 60% of 40 is 24.
Understanding Percentages: A Fundamental Concept
Percentages are a way of expressing a number as a fraction of 100. The word "percent" itself comes from the Latin "per centum," meaning "out of a hundred." This fundamental concept allows us to easily compare proportions and make relative comparisons across different datasets. Understanding percentages is essential for interpreting data, making informed decisions, and comprehending numerous aspects of our daily lives.
Alternative Methods for Calculating Percentages
While the decimal method is the most commonly used and efficient, there are other ways to calculate percentages, each with its own advantages depending on the context and individual preference:
-
Fraction Method: 60% can be expressed as the fraction 60/100, which can be simplified to 3/5. To find 60% of 40, we multiply 40 by 3/5: (3/5) * 40 = 24. This method can be particularly helpful when dealing with simpler percentages that easily translate into manageable fractions.
-
Proportion Method: This method sets up a proportion to solve for the unknown value. We can set up the proportion as follows:
x/40 = 60/100
Cross-multiplying and solving for x:
100x = 2400 x = 24
This method is helpful for visualizing the relationship between the percentage and the whole.
- Using a Calculator: Modern calculators have a percentage function (%) that simplifies the calculation. Simply enter 40, press the multiplication key (*), enter 60, press the percentage key (%), and the calculator will display the answer: 24. This method is efficient for quick calculations, especially with more complex percentages.
Real-World Applications of Percentages: Beyond the Classroom
Percentages permeate numerous aspects of our daily lives, making their understanding crucial for informed decision-making. Here are a few examples:
-
Finance: Percentages are fundamental in finance, used for calculating interest rates on loans and savings accounts, determining discounts on purchases, understanding tax rates, and analyzing investment returns. For example, calculating the interest earned on a savings account or the total cost of a product after sales tax involves percentage calculations. Understanding compound interest, which involves calculating interest on both the principal and accumulated interest, also relies heavily on percentages.
-
Sales and Marketing: Businesses extensively use percentages for pricing strategies, advertising promotions, and sales performance analysis. Discounts are typically expressed as percentages, and sales growth is often measured as a percentage increase or decrease compared to previous periods. Understanding these percentages allows consumers to make informed purchasing decisions, and allows businesses to strategize and track their progress effectively.
-
Science and Statistics: Percentages are essential tools for representing data in scientific studies and statistical analyses. Data is frequently presented as percentages to represent proportions, allowing for easier interpretation and comparison. For instance, researchers might use percentages to represent the percentage of a population affected by a disease or the success rate of a particular treatment. Statistical measures such as percentages, proportions, and ratios are used to analyze and present research findings.
-
Everyday Life: Percentages are ubiquitous in everyday situations, from calculating tips in restaurants to understanding nutritional information on food labels. Understanding the percentage of fat, carbohydrates, or protein in a food item can significantly impact dietary choices. Similarly, calculating a reasonable tip based on the total bill amount requires basic percentage knowledge.
Improving Your Percentage Calculation Skills: Tips and Tricks
Mastering percentage calculations doesn't require advanced mathematical skills, but consistent practice and a methodical approach can significantly improve your proficiency. Here are some helpful tips:
-
Memorize common percentage equivalents: Knowing the fraction and decimal equivalents of common percentages (e.g., 25% = 0.25 = 1/4, 50% = 0.5 = 1/2, 75% = 0.75 = 3/4) can significantly speed up calculations.
-
Practice regularly: Consistent practice is key to mastering any mathematical skill. Work through various percentage problems using different methods, gradually increasing the complexity of the problems.
-
Use visual aids: Diagrams and charts can help visualize percentage problems, making them easier to understand and solve, particularly when dealing with more complex scenarios.
-
Break down complex problems: Large or complicated percentage problems can often be broken down into smaller, more manageable steps, making the overall calculation more straightforward.
-
Check your work: Always double-check your answers using an alternative method to ensure accuracy. This helps catch errors and build confidence in your calculations.
Beyond the Basics: Advanced Percentage Applications
While calculating a simple percentage like 60% of 40 is straightforward, the applications of percentages extend far beyond basic calculations. More complex scenarios involve:
-
Percentage Change: This involves calculating the percentage increase or decrease between two values. For example, determining the percentage growth in sales from one year to the next requires calculating the percentage change.
-
Percentage Points: It's crucial to differentiate between percentage points and percentage change. A change from 10% to 20% is a 10 percentage point increase, but a 100% percentage increase. This distinction is vital for accurate interpretation of data.
-
Compound Interest: This involves calculating interest on both the principal amount and accumulated interest, resulting in exponential growth over time. Understanding compound interest is vital for long-term financial planning.
Conclusion: The Power of Percentages
The simple question of "What is 60 percent of 40?" serves as a gateway to understanding the power and versatility of percentages. This fundamental mathematical concept is indispensable in various fields, from everyday finances to complex scientific calculations. By mastering percentage calculations and understanding their diverse applications, you equip yourself with a valuable tool for navigating the numerical world around you, making informed decisions, and achieving success in various endeavors. Remember to practice regularly, explore different calculation methods, and always check your work to solidify your understanding and build confidence in your abilities. The ability to accurately and efficiently calculate percentages is a skill that will undoubtedly benefit you throughout your life.
Latest Posts
Latest Posts
-
What Is 3 10 In A Decimal
Apr 17, 2025
-
What Is A Factor Of 51
Apr 17, 2025
-
How Does An Igneous Rock Change To A Sedimentary Rock
Apr 17, 2025
-
Which Reaction Displays An Example Of An Arrhenius Base
Apr 17, 2025
-
How Many Feet Are In An Eighth Of A Mile
Apr 17, 2025
Related Post
Thank you for visiting our website which covers about What Is 60 Percent Of 40 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.