What Is 60 Percent Of 500
Kalali
Apr 07, 2025 · 5 min read
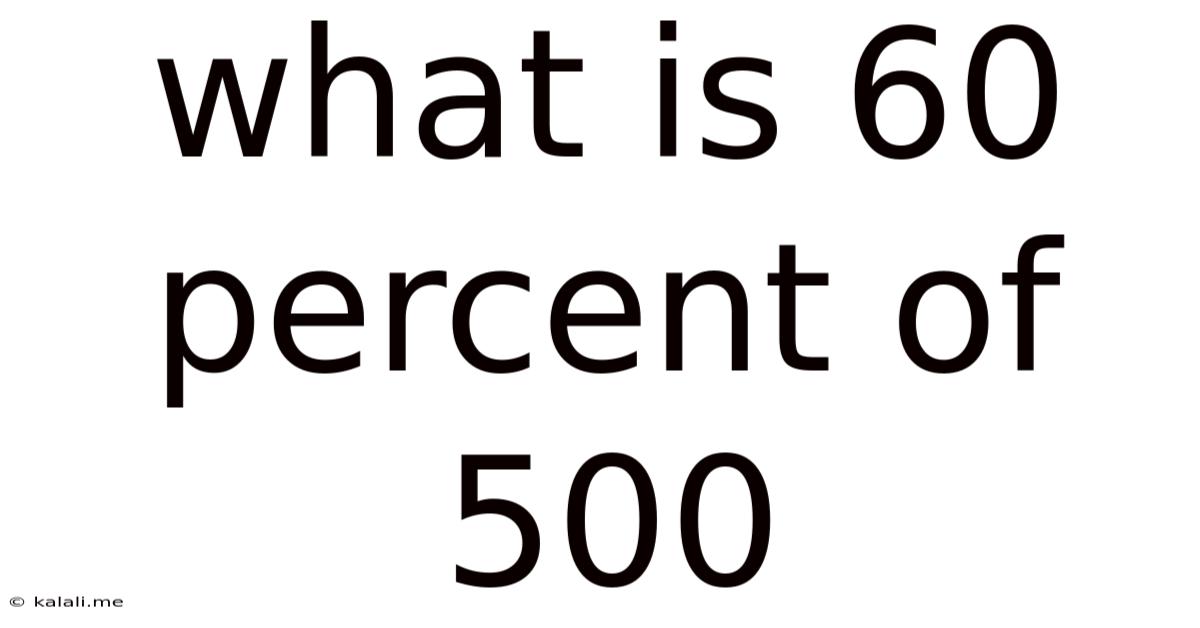
Table of Contents
What is 60 Percent of 500? A Deep Dive into Percentages and Their Applications
Finding 60 percent of 500 might seem like a simple arithmetic problem, but it opens the door to understanding a fundamental concept in mathematics and its widespread applications across various fields. This article delves into the calculation itself, explores different methods for solving percentage problems, and showcases the practical relevance of percentages in everyday life and professional settings.
Understanding Percentages: The Basics
A percentage is a fraction or a ratio expressed as a number out of 100. The term "percent" literally means "out of one hundred." For instance, 60 percent (60%) means 60 out of 100, which can be written as the fraction 60/100 or the decimal 0.60. Understanding this fundamental concept is crucial for tackling percentage calculations.
Calculating 60% of 500: The Straightforward Approach
The most direct way to calculate 60% of 500 involves converting the percentage to a decimal and then multiplying it by the given number.
-
Step 1: Convert the percentage to a decimal: 60% is equivalent to 60/100 = 0.60
-
Step 2: Multiply the decimal by the number: 0.60 * 500 = 300
Therefore, 60% of 500 is 300.
Alternative Methods for Calculating Percentages
While the method above is efficient, understanding alternative approaches offers flexibility and deeper insight into percentage calculations. Let's explore a few:
1. Using Fractions:
Percentages can be expressed as fractions. 60% can be written as 60/100, which simplifies to 3/5. To find 60% of 500, we can multiply 500 by the fraction 3/5:
(3/5) * 500 = 3 * (500/5) = 3 * 100 = 300
This method highlights the relationship between fractions and percentages.
2. Using Proportions:
Setting up a proportion is another effective method. We can set up a proportion as follows:
x / 500 = 60 / 100
To solve for x (60% of 500), we can cross-multiply:
100x = 60 * 500
100x = 30000
x = 30000 / 100
x = 300
This method emphasizes the concept of ratios and their equivalence.
3. Using a Calculator:
Most calculators have a percentage function (%) that simplifies the calculation. Simply enter 500, press the multiplication key, enter 60, and then press the percentage key. The calculator will automatically perform the calculation and display the result: 300. This method is particularly useful for more complex percentage calculations.
Real-World Applications of Percentage Calculations
Understanding percentages is essential in numerous real-world scenarios:
1. Finance and Budgeting:
- Interest Rates: Banks and financial institutions use percentages to calculate interest on loans and savings accounts. Understanding interest rates is crucial for making informed financial decisions.
- Discounts and Sales: Retailers frequently offer discounts expressed as percentages. Calculating the discounted price is a common application of percentage calculations. For example, a 20% discount on a $100 item means a saving of $20, resulting in a final price of $80.
- Taxes: Sales tax, income tax, and other taxes are often expressed as percentages of the purchase price or income. Accurate percentage calculations are crucial for determining tax obligations.
- Investment Returns: Investors track their investment returns as percentages to measure the growth or loss of their portfolio over time.
2. Science and Statistics:
- Data Analysis: Percentages are used extensively in data analysis to represent proportions and trends within datasets.
- Probability and Statistics: Percentages are used to express probabilities and statistical significance.
- Scientific Research: Experimental results are often reported as percentages to indicate the proportion of successful outcomes or significant findings.
3. Everyday Life:
- Tipping: Calculating tips in restaurants typically involves finding a percentage (e.g., 15% or 20%) of the bill.
- Cooking and Baking: Recipes often specify ingredients as percentages of the total weight or volume, particularly in professional baking and culinary arts.
- Grading Systems: Many educational systems use percentages to represent student grades, providing a standardized measure of academic performance.
4. Business and Economics:
- Market Share: Companies track their market share as a percentage to assess their position within a competitive landscape.
- Profit Margins: Businesses use percentages to calculate their profit margins, a key indicator of their financial health.
- Growth Rates: Economic growth, population growth, and other metrics are often expressed as percentages to track changes over time.
Advanced Percentage Problems and Their Solutions
Beyond the basic calculation of 60% of 500, many more complex percentage problems exist. Let's explore a few examples:
1. Finding the Original Amount:
If 60% of a number is 300, what is the original number?
We can set up an equation:
0.60x = 300
Solving for x:
x = 300 / 0.60 = 500
The original number is 500.
2. Finding the Percentage Increase or Decrease:
If a value increases from 500 to 600, what is the percentage increase?
Percentage increase = [(New Value - Old Value) / Old Value] * 100
Percentage increase = [(600 - 500) / 500] * 100 = (100 / 500) * 100 = 20%
The percentage increase is 20%.
3. Calculating Percentage Change with Multiple Increases or Decreases:
Consider a scenario involving multiple percentage changes. If a price increases by 10% and then decreases by 10%, the final price will not be the same as the original price due to the compounding effect of percentage changes.
Let’s say the original price is $100.
- 10% increase: $100 + ($100 * 0.10) = $110
- 10% decrease from $110: $110 - ($110 * 0.10) = $99
The final price is $99, demonstrating that percentage changes do not always cancel each other out.
4. Compound Interest Calculations:
Compound interest involves calculating interest not only on the principal amount but also on the accumulated interest from previous periods. This requires repeated percentage calculations over time. Understanding compound interest is crucial for long-term financial planning.
Conclusion: The Power of Percentages
The seemingly simple calculation of 60% of 500 unveils a vast world of applications for percentages. From everyday finances to complex scientific calculations and business strategies, percentages are an indispensable tool for representing proportions, making comparisons, and understanding change. Mastering percentage calculations empowers individuals to make informed decisions, analyze data effectively, and navigate the quantitative aspects of numerous fields. The diverse applications highlighted in this article showcase the significance of percentages as a fundamental mathematical concept with far-reaching implications.
Latest Posts
Latest Posts
-
How Many Kilometers Is In 10 Miles
Apr 09, 2025
-
How Long Is 33 Inches In Cm
Apr 09, 2025
-
Phone Number Not Allowed To Start With 911 Counting Problem
Apr 09, 2025
-
What Percent Is 7 Out Of 9
Apr 09, 2025
-
How Much Is Four Quarts Of Water
Apr 09, 2025
Related Post
Thank you for visiting our website which covers about What Is 60 Percent Of 500 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.