What Is 65 As A Fraction
Kalali
Apr 01, 2025 · 5 min read
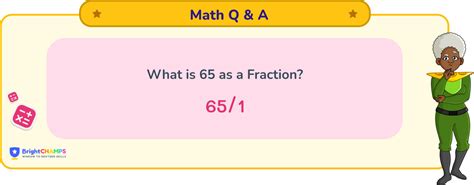
Table of Contents
What is 65 as a Fraction? A Comprehensive Guide
The question "What is 65 as a fraction?" might seem deceptively simple, but it opens the door to exploring several key concepts in mathematics, including fractions, simplification, and equivalent fractions. This comprehensive guide will not only answer this question but also delve into the underlying principles, offering a thorough understanding of fractions and their applications.
Understanding Fractions: A Quick Recap
Before we tackle the conversion of 65 to a fraction, let's refresh our understanding of fractions. A fraction represents a part of a whole. It's expressed as a ratio of two numbers: the numerator (the top number) and the denominator (the bottom number). The numerator indicates the number of parts we have, while the denominator indicates the total number of parts the whole is divided into.
For instance, the fraction 1/2 (one-half) represents one part out of two equal parts. Similarly, 3/4 (three-quarters) means three parts out of four equal parts.
Converting Whole Numbers to Fractions
Any whole number can be expressed as a fraction. The trick is to remember that any number divided by 1 remains unchanged. Therefore, to express a whole number as a fraction, we simply place the whole number as the numerator and 1 as the denominator.
Example: The whole number 5 can be expressed as the fraction 5/1. This represents five parts out of one equal part, which is essentially the whole number 5.
Expressing 65 as a Fraction
Following this principle, the whole number 65 can be expressed as a fraction in its simplest form as 65/1. This signifies 65 parts out of a single whole.
While 65/1 is the most straightforward representation, it's crucial to understand that numerous equivalent fractions exist. Equivalent fractions represent the same value, even though they appear different. They are created by multiplying or dividing both the numerator and the denominator by the same non-zero number.
Equivalent Fractions of 65/1
Let's explore some equivalent fractions of 65/1:
- Multiplying by 2: 65/1 * 2/2 = 130/2
- Multiplying by 3: 65/1 * 3/3 = 195/3
- Multiplying by 4: 65/1 * 4/4 = 260/4
- Multiplying by 5: 65/1 * 5/5 = 325/5
- And so on...
All these fractions – 130/2, 195/3, 260/4, 325/5, and countless others – are equivalent to 65/1. They all simplify back down to 65 when the numerator is divided by the denominator.
Simplifying Fractions
Simplifying a fraction means reducing it to its lowest terms. This involves finding the greatest common divisor (GCD) of the numerator and denominator and dividing both by it. The GCD is the largest number that divides both the numerator and the denominator without leaving a remainder.
For example, let's simplify the fraction 130/2. The GCD of 130 and 2 is 2. Dividing both the numerator and denominator by 2 gives us: 130/2 = 65/1
The fraction 65/1, however, is already in its simplest form, as the GCD of 65 and 1 is 1. There are no common factors other than 1.
Applications of Fractions: Real-World Examples
Understanding fractions is essential in various aspects of daily life:
- Cooking and Baking: Recipes often call for fractional amounts of ingredients, such as 1/2 cup of sugar or 2/3 cup of flour.
- Measurement: We use fractions when measuring lengths, weights, and volumes. For example, a board might be 2 1/4 inches thick, or a container might hold 1 1/2 liters of liquid.
- Finance: Fractions are integral to understanding percentages, interest rates, and stock prices.
- Geometry: Fractions are used extensively in geometric calculations, such as finding the area of a triangle or the volume of a sphere.
Beyond the Basics: Improper Fractions and Mixed Numbers
While 65/1 is a proper fraction (the numerator is less than the denominator), it's also important to understand improper fractions and mixed numbers.
- Improper Fraction: An improper fraction is one where the numerator is greater than or equal to the denominator (e.g., 7/4).
- Mixed Number: A mixed number combines a whole number and a proper fraction (e.g., 1 3/4).
Converting between improper fractions and mixed numbers is a valuable skill. To convert an improper fraction to a mixed number, divide the numerator by the denominator. The quotient becomes the whole number part, and the remainder becomes the numerator of the proper fraction. The denominator remains the same.
For example, let's convert 7/4 to a mixed number:
7 ÷ 4 = 1 with a remainder of 3. Therefore, 7/4 = 1 3/4.
Conversely, to convert a mixed number to an improper fraction, multiply the whole number by the denominator, add the numerator, and place the result over the original denominator.
For example, let's convert 1 3/4 to an improper fraction:
(1 * 4) + 3 = 7. Therefore, 1 3/4 = 7/4
Advanced Fraction Concepts: Decimals and Percentages
Fractions, decimals, and percentages are all interconnected. They represent different ways of expressing parts of a whole. It's often beneficial to convert between these formats.
To convert a fraction to a decimal, divide the numerator by the denominator. For instance, 1/2 = 0.5, and 3/4 = 0.75.
To convert a decimal to a fraction, place the decimal value over 1 and then multiply the numerator and denominator by a power of 10 to eliminate the decimal point. For example, 0.5 can be written as 5/10, which simplifies to 1/2.
To convert a fraction to a percentage, convert it to a decimal first, and then multiply by 100 and add the percent symbol (%). For example, 1/2 = 0.5 * 100% = 50%.
Conclusion: Mastering Fractions
This detailed exploration of "What is 65 as a fraction?" has revealed much more than a simple conversion. We've delved into the fundamental principles of fractions, explored equivalent fractions and simplification, and highlighted the numerous practical applications of fractions in our daily lives. A strong understanding of fractions is a cornerstone of mathematical proficiency, extending far beyond basic arithmetic. By grasping the concepts discussed here, you'll be well-equipped to tackle more complex mathematical problems and to confidently use fractions in various real-world scenarios. Remember, practice is key! The more you work with fractions, the more comfortable and proficient you will become.
Latest Posts
Latest Posts
-
How Many Centimeters Are In 8 Feet
Apr 02, 2025
-
Do Elements In The Same Period Have Similar Properties
Apr 02, 2025
-
How Big Is 24 Cm In Inches
Apr 02, 2025
-
How Many Ml Are In 60 Oz
Apr 02, 2025
-
Cuanto Es El 60 Por Ciento
Apr 02, 2025
Related Post
Thank you for visiting our website which covers about What Is 65 As A Fraction . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
