What Is 7 16 In Decimal
Kalali
Apr 05, 2025 · 5 min read
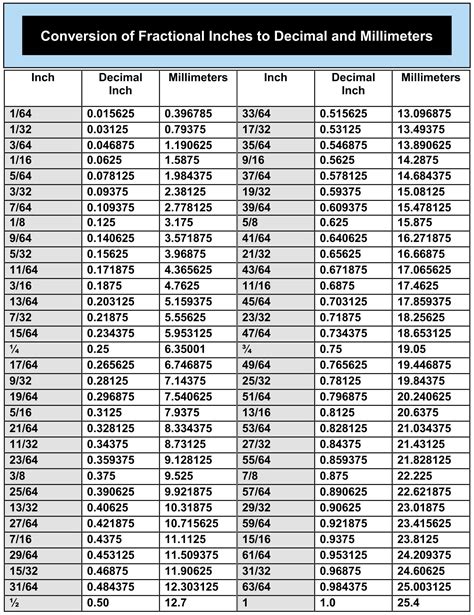
Table of Contents
What is 7/16 in Decimal? A Comprehensive Guide to Fraction-to-Decimal Conversion
Converting fractions to decimals is a fundamental skill in mathematics with applications spanning various fields. Understanding this process is crucial for anyone working with numbers, from students tackling basic arithmetic to professionals using data analysis in their careers. This comprehensive guide dives deep into the conversion of the fraction 7/16 to its decimal equivalent, exploring various methods and providing a deeper understanding of the underlying principles.
Understanding Fractions and Decimals
Before we delve into the conversion of 7/16, let's refresh our understanding of fractions and decimals.
Fractions represent parts of a whole. They consist of two parts: a numerator (the top number) and a denominator (the bottom number). The numerator indicates the number of parts we have, while the denominator indicates the total number of equal parts the whole is divided into.
Decimals represent numbers that are not whole numbers. They are based on the powers of 10, with each digit to the right of the decimal point representing a decreasing power of 10 (tenths, hundredths, thousandths, and so on).
Method 1: Long Division
The most straightforward method to convert a fraction to a decimal is through long division. We divide the numerator (7) by the denominator (16).
Steps:
-
Set up the long division: Place the numerator (7) inside the division symbol and the denominator (16) outside. Since 7 is smaller than 16, we add a decimal point to 7 and a zero, making it 7.0.
-
Divide: 16 goes into 70 four times (16 x 4 = 64). Write the 4 above the decimal point and subtract 64 from 70, leaving a remainder of 6.
-
Add a zero: Add another zero to the remainder (6), making it 60.
-
Continue dividing: 16 goes into 60 three times (16 x 3 = 48). Write the 3 after the 4 and subtract 48 from 60, leaving a remainder of 12.
-
Repeat: Add another zero to the remainder (12), making it 120. 16 goes into 120 seven times (16 x 7 = 112). Write the 7 after the 3 and subtract 112 from 120, leaving a remainder of 8.
-
Continue the process: This process can continue indefinitely, as 16 will never divide evenly into 8. However, we notice a pattern: we will keep getting remainders and the digits will repeat. Let's continue a few more steps to illustrate:
- Add another zero to 8 (making it 80). 16 goes into 80 five times (16 x 5 = 80). The remainder is 0, and the division terminates.
-
Result: The decimal equivalent of 7/16 is 0.4375.
Method 2: Using Equivalent Fractions
Another approach involves converting the fraction to an equivalent fraction with a denominator that is a power of 10. While this isn't always possible (as in this case), it's a useful technique for certain fractions. Unfortunately, 16 cannot be easily converted to a power of 10. We would need to multiply by a number that contains factors of 2 and 5 to achieve this, and no such simple conversion exists.
Method 3: Utilizing a Calculator
The easiest method, especially for complex fractions, is to use a calculator. Simply enter 7 ÷ 16 and the calculator will display the decimal equivalent, 0.4375. This method is quick and efficient but lacks the educational value of the long division method.
Understanding the Decimal Representation: Terminating vs. Repeating Decimals
The decimal representation of 7/16 is a terminating decimal, meaning the decimal representation ends after a finite number of digits. Not all fractions result in terminating decimals. Fractions with denominators that contain only factors of 2 and 5 will always result in terminating decimals. Fractions with denominators containing other prime factors (such as 3, 7, 11, etc.) will result in repeating decimals, where a sequence of digits repeats infinitely.
Practical Applications of Decimal Conversions
The ability to convert fractions to decimals is critical in various fields:
- Engineering and Construction: Precise measurements and calculations often require converting fractions (e.g., inches) to decimals for accurate computations.
- Finance and Accounting: Dealing with percentages, interest rates, and financial calculations frequently involves converting fractions to decimals.
- Data Analysis and Statistics: Many statistical calculations require data in decimal format.
- Computer Science and Programming: Representing numbers and performing calculations in computer systems often involves working with decimal numbers.
- Everyday Life: Numerous everyday situations involve the need to convert fractions to decimals, such as calculating tips, dividing portions of food, or measuring ingredients in recipes.
Beyond 7/16: Generalizing the Fraction-to-Decimal Conversion
The methods discussed for converting 7/16 can be applied to any fraction. The long division method is particularly versatile and applicable to any fraction, whether it results in a terminating or repeating decimal. Remember to be patient and methodical when performing long division, ensuring accuracy in each step.
The ability to convert fractions to decimals isn't just about getting the right answer; it's about understanding the fundamental relationship between these two representations of numbers. It's about grasping the underlying mathematical principles and appreciating the practical applications of this essential skill across diverse fields.
Troubleshooting Common Mistakes in Decimal Conversion
Several common errors can occur when converting fractions to decimals. Let's address some of them:
- Incorrect placement of the decimal point: Carefully align the decimal point in the quotient (the result of the division) above the decimal point in the dividend (the numerator).
- Errors in subtraction: Double-check your subtraction steps during long division to avoid cumulative errors.
- Misunderstanding of remainders: Understand that remainders in long division are continued by adding zeros to the right of the decimal point, not simply discarding them.
- Incorrect rounding: If you need to round a repeating decimal, understand the rules of rounding to avoid inaccurate representations.
By understanding these potential pitfalls and following the steps outlined carefully, you can accurately and confidently convert fractions to decimals. Mastering this skill is a valuable asset in various aspects of life, from academic pursuits to professional work. The seemingly simple conversion of 7/16 into its decimal equivalent serves as a gateway to a deeper understanding of numbers and their representation.
Latest Posts
Latest Posts
-
10 To The Power Of 20
Apr 06, 2025
-
How Many Cups In 32 Fluid Ounces
Apr 06, 2025
-
1 Metro 72 Cm In Feet
Apr 06, 2025
-
What Is Ten Percent Of 200
Apr 06, 2025
-
What 38 6 Degrees Celsius In Fahrenheit
Apr 06, 2025
Related Post
Thank you for visiting our website which covers about What Is 7 16 In Decimal . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
