What Is 7/6 As A Mixed Number
Kalali
Apr 23, 2025 · 5 min read
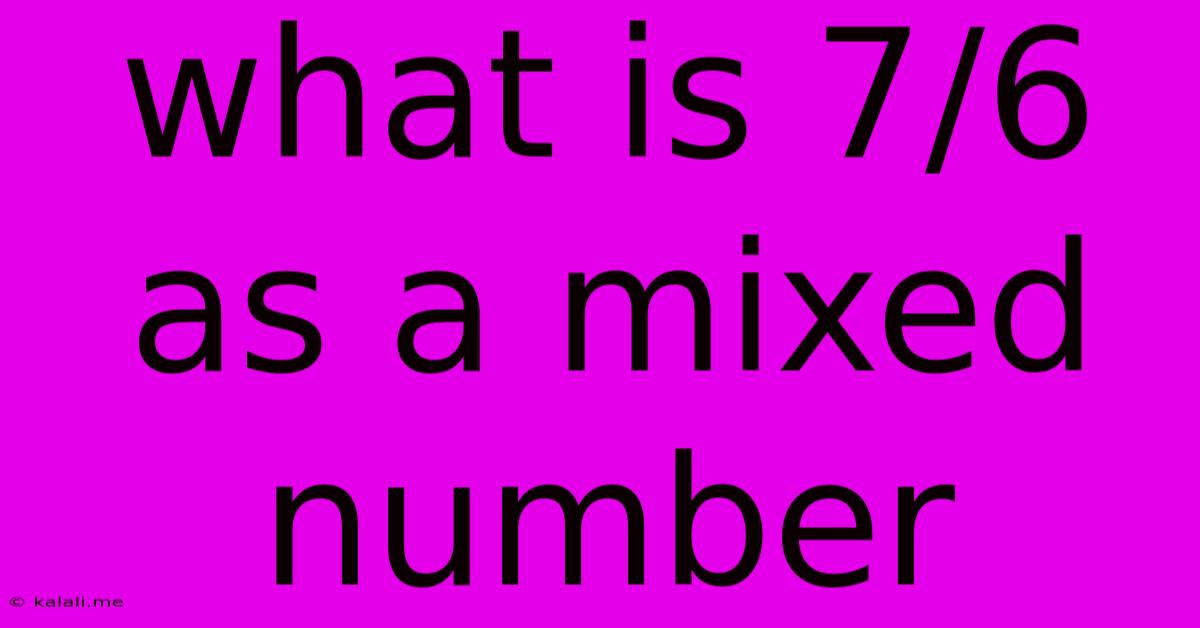
Table of Contents
What is 7/6 as a Mixed Number? A Comprehensive Guide to Fraction Conversion
Understanding fractions is fundamental to mathematics, and converting improper fractions (like 7/6) into mixed numbers is a crucial skill. This comprehensive guide will not only show you how to convert 7/6 to a mixed number but will also delve into the underlying concepts, providing you with a solid foundation for tackling similar fraction conversions. We'll explore various methods, offer practice problems, and discuss the importance of mastering this skill. This guide aims to be your complete resource for understanding and confidently converting improper fractions to mixed numbers.
Meta Description: Learn how to convert the improper fraction 7/6 into a mixed number. This comprehensive guide explains the process, provides examples, and explores the underlying concepts of fraction conversion. Master fraction manipulation with this in-depth tutorial.
Understanding Fractions: A Quick Refresher
Before diving into the conversion, let's quickly review the basics of fractions. A fraction represents a part of a whole. It consists of two main components:
- Numerator: The top number represents the number of parts you have.
- Denominator: The bottom number represents the total number of equal parts the whole is divided into.
In the fraction 7/6, 7 is the numerator and 6 is the denominator. This is an improper fraction because the numerator (7) is larger than the denominator (6). Improper fractions represent a value greater than one. Mixed numbers, on the other hand, combine a whole number and a proper fraction (where the numerator is smaller than the denominator). Converting improper fractions to mixed numbers makes it easier to visualize and understand the quantity represented.
Method 1: Long Division
The most straightforward method to convert an improper fraction like 7/6 into a mixed number is using long division. This method provides a clear visual representation of the process and is easily understood.
- Divide the numerator by the denominator: Divide 7 by 6.
- Determine the whole number: The quotient (the result of the division) represents the whole number part of your mixed number. 7 divided by 6 is 1 with a remainder. Therefore, the whole number is 1.
- Determine the remainder: The remainder from the division becomes the numerator of the fractional part of your mixed number. The remainder in this case is 1.
- Keep the original denominator: The denominator of the fraction in your mixed number remains the same as the denominator of the original improper fraction. The denominator remains 6.
- Combine the whole number and the fraction: Put the whole number and the fraction together to form the mixed number.
Therefore, 7/6 as a mixed number is 1 1/6.
Method 2: Visual Representation
While long division provides a procedural approach, visualizing the fraction can enhance understanding. Imagine you have 7 slices of pizza, and each pizza is cut into 6 slices.
- Form whole pizzas: You can assemble one complete pizza (6 slices).
- Remaining slices: You have 1 slice left over.
- Mixed number representation: This translates to 1 whole pizza and 1/6 of a pizza, represented as 1 1/6.
Method 3: Subtracting the Denominator Repeatedly
This method involves repeatedly subtracting the denominator from the numerator until the result is less than the denominator.
- Subtract the denominator: Start by subtracting the denominator (6) from the numerator (7). 7 - 6 = 1.
- Count the subtractions: The number of times you successfully subtract the denominator represents the whole number part of your mixed number. We subtracted 6 once, so the whole number is 1.
- Remaining value: The remaining value after the subtraction becomes the numerator of the fraction part of your mixed number (1).
- Maintain the denominator: The denominator remains 6.
This results in the mixed number 1 1/6.
Why is Converting Improper Fractions Important?
Converting improper fractions to mixed numbers offers several advantages:
- Improved Understanding: Mixed numbers are often easier to visualize and interpret than improper fractions. It's easier to grasp the concept of "1 and 1/6 pizzas" than "7/6 pizzas".
- Easier Calculations: In certain mathematical operations, particularly addition and subtraction, mixed numbers can simplify the process.
- Real-World Applications: Many real-world scenarios involve quantities that are best represented as mixed numbers. Think about measuring ingredients in a recipe or calculating distances.
Practice Problems
Let's solidify your understanding with some practice problems. Convert the following improper fractions into mixed numbers:
- 11/4
- 15/8
- 22/7
- 9/2
- 17/5
Solutions:
- 11/4 = 2 ¾
- 15/8 = 1 ⅞
- 22/7 = 3 1/7
- 9/2 = 4 ½
- 17/5 = 3 ⅖
Advanced Concepts and Further Exploration
Once you've mastered converting simple improper fractions, you can explore more advanced concepts:
- Converting Mixed Numbers to Improper Fractions: This is the reverse process, and understanding both conversions is crucial for fluency in fraction manipulation.
- Operations with Mixed Numbers: Learn how to add, subtract, multiply, and divide mixed numbers.
- Fractions and Decimals: Understand the relationship between fractions and decimals and how to convert between them.
- Working with Negative Fractions: Expand your skills to include negative improper fractions and their mixed number equivalents.
Conclusion
Converting 7/6 to the mixed number 1 1/6 is a fundamental step in understanding and working with fractions. By understanding the different methods – long division, visualization, and repeated subtraction – you can confidently tackle any improper fraction conversion. Remember that mastering fraction manipulation is a building block for more advanced mathematical concepts. Practice regularly, explore advanced concepts, and soon you’ll be a fraction expert! This comprehensive guide serves as a solid foundation for your journey in mastering fraction conversion and developing a strong understanding of mathematical principles. Remember to practice regularly to solidify your understanding and build confidence in your skills.
Latest Posts
Latest Posts
-
What Percentage Is 2 3 Of 100
May 09, 2025
-
48 Out Of 50 As A Percentage
May 09, 2025
-
Which Function Has No Horizontal Asymptote
May 09, 2025
-
How Many Hours Is 136 Minutes
May 09, 2025
-
What Happens When An Oceanic And Oceanic Plate Collide
May 09, 2025
Related Post
Thank you for visiting our website which covers about What Is 7/6 As A Mixed Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.