What Is 7/9 As A Percentage
Kalali
Apr 05, 2025 · 4 min read
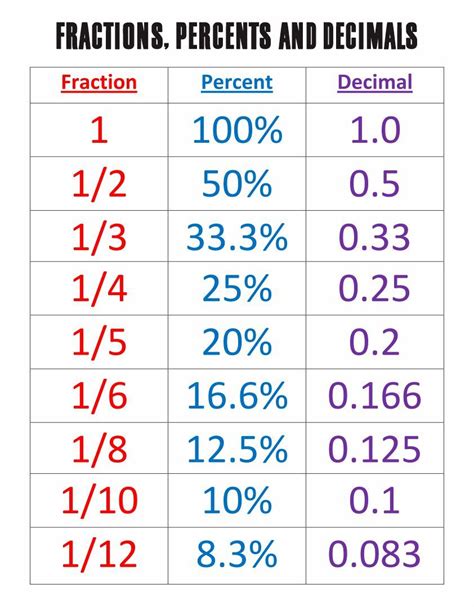
Table of Contents
What is 7/9 as a Percentage? A Comprehensive Guide
Converting fractions to percentages is a fundamental skill in mathematics with applications across various fields, from finance and statistics to everyday calculations. This comprehensive guide will delve into the process of converting the fraction 7/9 into a percentage, explaining the steps involved and providing additional context to enhance your understanding. We'll also explore related concepts and offer practical examples to solidify your grasp of this important mathematical operation.
Understanding Fractions and Percentages
Before diving into the conversion, let's establish a solid understanding of fractions and percentages.
Fractions: A fraction represents a part of a whole. It's expressed as a ratio of two numbers: the numerator (top number) and the denominator (bottom number). In the fraction 7/9, 7 is the numerator and 9 is the denominator. This means we have 7 parts out of a total of 9 parts.
Percentages: A percentage is a way of expressing a number as a fraction of 100. The symbol "%" represents "per cent," meaning "out of 100." For example, 50% means 50 out of 100, which is equivalent to the fraction 50/100 or the decimal 0.5.
Converting 7/9 to a Percentage: The Step-by-Step Process
There are two primary methods to convert the fraction 7/9 into a percentage:
Method 1: Using Division
This method involves dividing the numerator by the denominator and then multiplying the result by 100.
-
Divide the numerator by the denominator: 7 ÷ 9 = 0.777... (This is a recurring decimal).
-
Multiply the result by 100: 0.777... × 100 = 77.777...%
Therefore, 7/9 is approximately 77.78%. We round to two decimal places for practical purposes.
Method 2: Finding an Equivalent Fraction with a Denominator of 100
This method involves finding an equivalent fraction where the denominator is 100. While not always possible to achieve a precise equivalent with a denominator of 100 (as in this case), it's a valuable technique for understanding the underlying principle.
-
Set up a proportion: We need to find a number 'x' such that: 7/9 = x/100
-
Solve for x: To solve for 'x', we can cross-multiply: 9x = 700
-
Calculate x: x = 700/9 ≈ 77.78
Therefore, 7/9 is approximately equivalent to 77.78/100, which is 77.78%.
Understanding Recurring Decimals and Rounding
The conversion of 7/9 to a percentage results in a recurring decimal (0.777...). This means the digit 7 repeats infinitely. In practical applications, we need to round the decimal to a certain number of decimal places. Rounding to two decimal places gives us 77.78%, which is a commonly accepted level of precision. However, it's important to remember that this is an approximation; the true value is slightly more than 77.77%.
Practical Applications of Percentage Conversions
The ability to convert fractions to percentages is vital in numerous real-world scenarios:
- Finance: Calculating interest rates, discounts, profit margins, and tax percentages.
- Statistics: Representing data proportions and probabilities.
- Science: Expressing experimental results and measurement errors.
- Everyday Life: Determining tips, sales discounts, and comparing different values.
Further Exploration: Working with Percentages
Beyond the conversion of 7/9 to a percentage, let's explore some related concepts:
Finding a Percentage of a Number
To find a percentage of a number, you multiply the number by the percentage (expressed as a decimal).
For example, to find 77.78% of 200:
0.7778 × 200 = 155.56
Converting Percentages to Fractions and Decimals
Converting percentages to fractions and decimals is the reverse process of what we've been doing.
-
Percentage to Decimal: Divide the percentage by 100. For example, 77.78% = 77.78/100 = 0.7778
-
Percentage to Fraction: Write the percentage as a fraction with a denominator of 100, and then simplify if possible. For example, 77.78% ≈ 7778/10000 = 3889/5000
Percentage Increase and Decrease
Percentage increase or decrease measures the relative change between two values.
-
Percentage Increase: [(New Value - Old Value) / Old Value] × 100%
-
Percentage Decrease: [(Old Value - New Value) / Old Value] × 100%
Advanced Applications: Using Spreadsheets and Programming
Software like Microsoft Excel or Google Sheets provides built-in functions for converting fractions to percentages and performing various percentage calculations. Programming languages also offer functions to simplify these operations.
Conclusion: Mastering Percentage Conversions
Converting fractions to percentages is a cornerstone of mathematical literacy. Understanding the process, as demonstrated with the conversion of 7/9 to approximately 77.78%, equips you with a practical skill applicable across numerous contexts. Mastering this skill enhances your ability to interpret data, solve problems, and make informed decisions in various aspects of life and professional endeavors. Remember to practice regularly, explore different methods, and understand the implications of rounding and recurring decimals for a truly comprehensive understanding.
Latest Posts
Latest Posts
-
167 Cm Is How Many Inches
Apr 06, 2025
-
What Percent Is 3 Of 15
Apr 06, 2025
-
How Many Sides Do A Pyramid Have
Apr 06, 2025
-
How Many Oz Is 1 Cup Butter
Apr 06, 2025
-
17 Out Of 23 As A Percentage
Apr 06, 2025
Related Post
Thank you for visiting our website which covers about What Is 7/9 As A Percentage . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
