What Is 7 To The Power Of 3
Kalali
Apr 16, 2025 · 6 min read
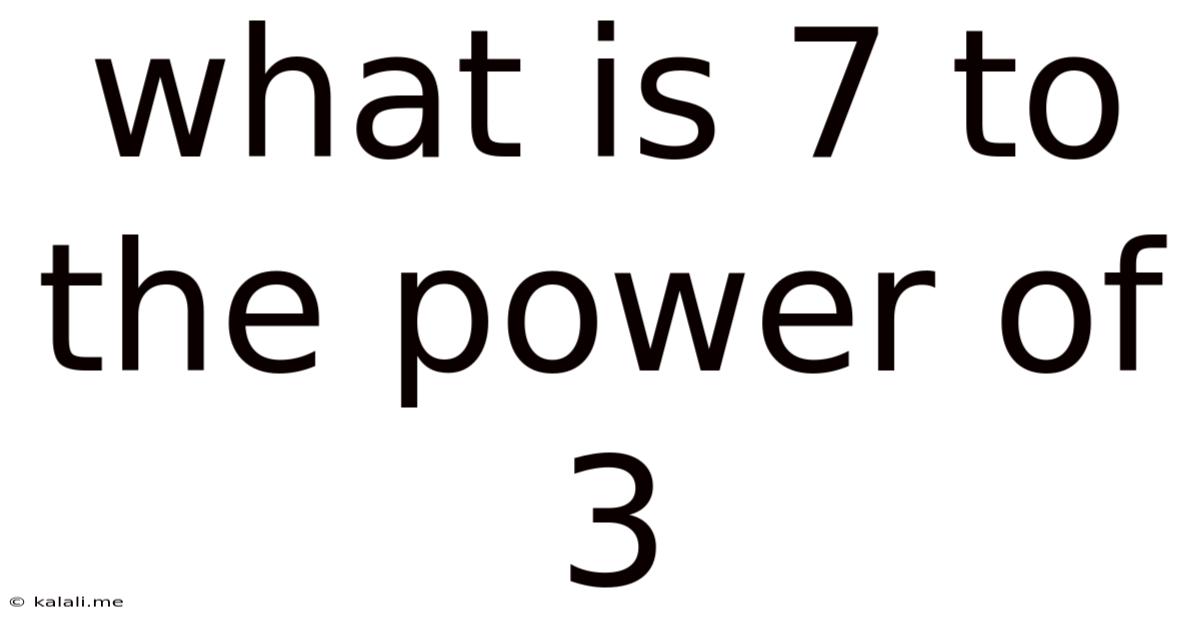
Table of Contents
What is 7 to the Power of 3? Unpacking Exponents and Their Applications
What is 7 to the power of 3? The simple answer is 343. But this seemingly straightforward mathematical operation opens a door to a fascinating world of exponents, their properties, and their widespread applications across various fields. This article delves deep into understanding 7 cubed, exploring the concept of exponents, demonstrating different calculation methods, and showcasing the relevance of exponential notation in real-world scenarios. We'll also touch upon related mathematical concepts and address common misconceptions.
Meta Description: Discover the answer to "What is 7 to the power of 3?" This comprehensive guide explains exponents, provides multiple ways to calculate 7³, and explores real-world applications of exponential notation in various fields, from finance to physics.
Understanding Exponents (Powers or Indices)
Before diving into the specifics of 7³, let's establish a firm understanding of exponents. An exponent, also known as a power or index, indicates how many times a number (the base) is multiplied by itself. In the expression bⁿ, 'b' represents the base, and 'n' represents the exponent. This expression reads as "b to the power of n" or "b raised to the power of n".
For example:
- 2² = 2 x 2 = 4 (2 to the power of 2, or 2 squared)
- 3³ = 3 x 3 x 3 = 27 (3 to the power of 3, or 3 cubed)
- 5⁴ = 5 x 5 x 5 x 5 = 625 (5 to the power of 4, or 5 to the fourth power)
In our case, "7 to the power of 3" (or 7³) means 7 multiplied by itself three times: 7 x 7 x 7 = 343.
Methods for Calculating 7³
While the answer is straightforward, let's explore different methods for calculating 7³ to enhance your understanding of mathematical operations:
1. Direct Multiplication: This is the most basic approach, as demonstrated above: 7 x 7 = 49; 49 x 7 = 343. This method is suitable for smaller exponents and bases.
2. Using a Calculator: Most calculators have an exponent function (usually denoted as x^y or ^). Simply input 7, press the exponent button, enter 3, and press equals (=). This provides a quick and efficient solution, especially for larger numbers or exponents.
3. Utilizing Logarithms (for advanced users): Logarithms provide an alternative method, though it's generally less efficient for this specific problem. The logarithm of a number is the exponent to which another fixed value, the base, must be raised to produce that number. While this method isn't necessary for calculating 7³, it's a valuable tool for solving more complex exponential equations.
4. Mental Calculation Techniques: With practice, you can develop mental math strategies. For example, you could break down the calculation: 7 x 7 = 49; then, 49 x 7 can be approached as (50 - 1) x 7 = 350 - 7 = 343. This method helps improve mental arithmetic skills.
The Significance of 7³ in Different Contexts
The number 343, the result of 7³, appears in various mathematical contexts and real-world applications:
-
Geometry: 343 could represent the volume of a cube with sides of length 7 units. Volume calculations frequently involve exponents, particularly when dealing with three-dimensional shapes.
-
Number Theory: Within number theory, 343 holds significance as a perfect cube (7³). It's also a composite number, meaning it has factors other than 1 and itself. Exploring its prime factorization (7 x 7 x 7) reveals valuable insights into its divisibility properties.
-
Combinatorics and Probability: Exponential functions often appear in combinatorics problems, dealing with counting arrangements and probabilities. While 7³ itself might not directly appear in a specific formula, the underlying principles of exponents are crucial in these calculations.
-
Computer Science: Binary numbers (base-2) and other numerical systems use exponential notation extensively in representing data and performing calculations. While base 7 isn't as prevalent as base 2 or 10, understanding exponents is fundamental to computer science.
-
Physics and Engineering: Exponential functions model various phenomena, including radioactive decay, population growth, and the behavior of electrical circuits. Understanding exponential growth and decay is crucial in these fields. While 7³ may not be a direct constant in these equations, the concept of exponents forms the core of these mathematical models.
Expanding on Exponent Rules
Understanding the basic concept of exponents is just the beginning. Several rules govern exponential operations, allowing for simplification and efficient calculations:
-
Product Rule: When multiplying two exponential expressions with the same base, you add the exponents:
bᵐ x bⁿ = b^(m+n) -
Quotient Rule: When dividing two exponential expressions with the same base, you subtract the exponents:
bᵐ / bⁿ = b^(m-n) -
Power Rule: When raising an exponential expression to another power, you multiply the exponents:
(bᵐ)ⁿ = b^(m x n) -
Zero Exponent Rule: Any non-zero number raised to the power of 0 is equal to 1:
b⁰ = 1 -
Negative Exponent Rule: A negative exponent indicates the reciprocal of the base raised to the positive exponent:
b⁻ⁿ = 1/bⁿ
These rules are critical for simplifying complex expressions involving exponents and solving equations. Mastering these rules will significantly enhance your mathematical abilities.
Addressing Common Misconceptions about Exponents
Several common misunderstandings surrounding exponents need clarification:
-
Misconception 1:
(a + b)² ≠ a² + b²It's crucial to remember that squaring a sum (or any power) doesn't distribute to each term. The correct expansion is(a + b)² = a² + 2ab + b². -
Misconception 2:
a⁻¹ ≠ -aA negative exponent does not imply a negative number. Instead, it represents the reciprocal.a⁻¹ = 1/a.
Understanding these misconceptions will prevent errors in calculations and ensure accuracy.
Real-World Applications of Exponential Functions
Exponential functions are ubiquitous, appearing in diverse fields:
-
Finance: Compound interest calculations rely heavily on exponential functions. The formula for compound interest involves raising the principal amount to a power based on the interest rate and the number of compounding periods.
-
Biology: Population growth (or decay) in biological systems often follows exponential patterns. Understanding exponential growth is vital in modeling population dynamics.
-
Physics: Radioactive decay, the gradual decrease in the amount of a radioactive substance over time, is described by an exponential decay function.
-
Chemistry: Chemical reactions sometimes exhibit exponential behavior.
These examples highlight the significance of understanding exponential functions in various scientific and practical disciplines.
Conclusion: Beyond 7³
While answering the initial question – what is 7 to the power of 3? – with the result 343 is relatively simple, the underlying principles of exponents are far-reaching and incredibly important. This exploration extends beyond a single calculation, providing a foundational understanding of exponential notation, calculation methods, relevant mathematical rules, common misconceptions, and the vast array of real-world applications where exponential functions play a crucial role. Mastering exponents opens doors to advanced mathematical concepts and problem-solving across various fields. The journey from understanding 7³ to grasping the power of exponential functions is a significant step in enhancing mathematical literacy and problem-solving skills.
Latest Posts
Latest Posts
-
What Is 1 8 Of 100
Apr 19, 2025
-
What Is 25 Fahrenheit In Celsius
Apr 19, 2025
-
What Percent Of 500 Is 400
Apr 19, 2025
-
How Many Cups Is 20 Fl Oz
Apr 19, 2025
Related Post
Thank you for visiting our website which covers about What Is 7 To The Power Of 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.