What Is 70 Percent Of 15
Kalali
Apr 26, 2025 · 5 min read
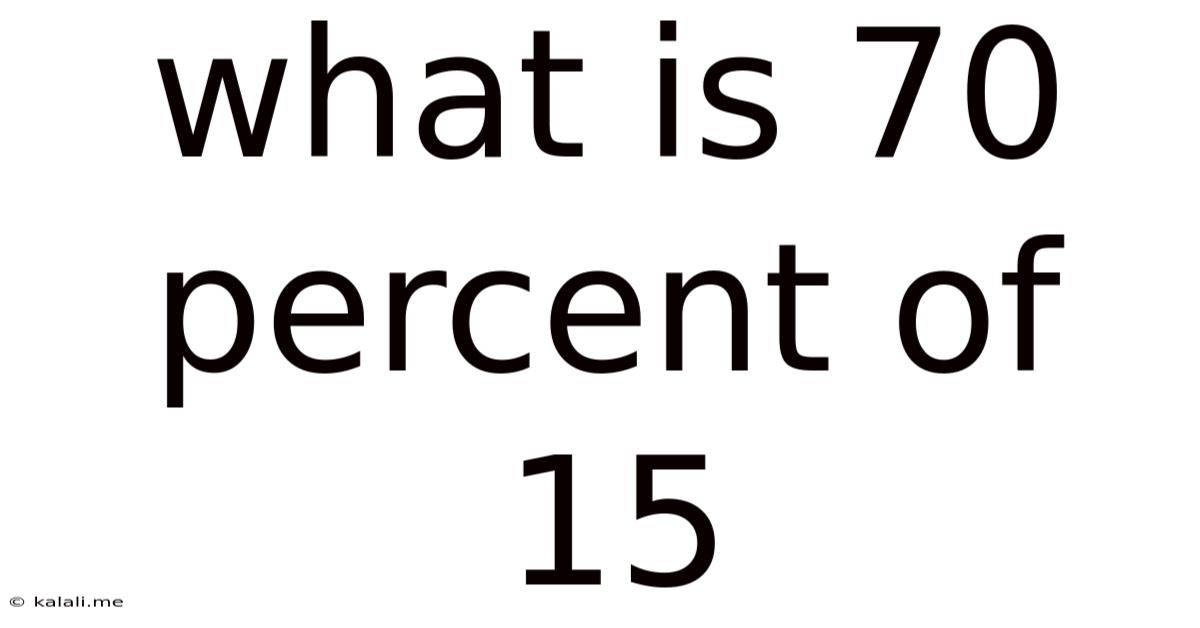
Table of Contents
What is 70 Percent of 15? A Deep Dive into Percentage Calculations and Their Applications
Finding 70% of 15 might seem like a simple arithmetic problem, but understanding the underlying concepts opens doors to a vast world of applications in various fields. This article will not only answer the question directly but also explore the various methods of calculating percentages, delve into the practical uses of percentage calculations, and touch upon the historical significance of percentages. By the end, you'll have a comprehensive understanding of percentages and their importance in everyday life and beyond.
Meta Description: Learn how to calculate 70% of 15 and discover the versatile applications of percentages in various fields, from everyday finances to advanced statistical analysis. This comprehensive guide unravels the intricacies of percentage calculations with clear explanations and real-world examples.
Calculating 70% of 15: The Basic Approach
The most straightforward way to find 70% of 15 is to convert the percentage to a decimal and then multiply. 70% can be written as 0.70 (or simply 0.7). Therefore:
0.7 * 15 = 10.5
Therefore, 70% of 15 is 10.5.
Alternative Methods for Calculating Percentages
While the above method is the most common, several other methods can achieve the same result, each offering unique advantages depending on the context:
-
Using Fractions: Percentages can be expressed as fractions. 70% is equivalent to 70/100, which simplifies to 7/10. Therefore, to find 70% of 15, we can calculate (7/10) * 15 = 10.5. This method is useful when dealing with simpler percentages that can be easily converted into fractions.
-
Proportions: We can set up a proportion: 70/100 = x/15. Cross-multiplying gives us 100x = 70 * 15. Solving for x, we get x = (70 * 15) / 100 = 10.5. This approach is helpful for understanding the proportional relationship between the percentage and the whole.
-
Using a Calculator: Most calculators have a percentage function (%) that directly computes percentages. Simply enter 15, press the multiplication key (*), enter 70, and then press the percentage key (%). The calculator will automatically perform the calculation and display the result, 10.5. This method is the quickest and most efficient for everyday calculations.
Understanding the Concept of Percentages
Percentages are a way of expressing a number as a fraction of 100. They are widely used to represent proportions, rates, and changes in various contexts. The word "percent" comes from the Latin phrase "per centum," meaning "out of a hundred." This inherently links percentages to the concept of fractions and ratios.
Understanding percentages is crucial for interpreting data presented in various formats, making informed decisions, and understanding the world around us. From understanding sales tax to comprehending interest rates, percentages are ubiquitous in our daily lives.
Real-World Applications of Percentage Calculations
The ability to calculate percentages efficiently is a valuable skill with applications across various disciplines:
-
Finance: Calculating interest on loans, mortgages, and savings accounts relies heavily on percentage calculations. Understanding interest rates and compound interest requires a strong grasp of percentage concepts. Analyzing investment returns, profit margins, and discounts also involves percentage computations.
-
Sales and Marketing: Determining discounts, sales tax, and profit margins are essential aspects of sales and marketing. Analyzing sales data and market share often involves comparing percentages. Effective pricing strategies and promotional campaigns depend on understanding how percentages affect customer perception and purchasing behavior.
-
Statistics and Data Analysis: Percentages are fundamental to statistical analysis. Expressing data as percentages allows for easier comparison and interpretation of different datasets. Calculating percentages is crucial in understanding trends, making predictions, and drawing meaningful conclusions from data.
-
Science and Engineering: Percentage calculations are used extensively in scientific and engineering applications. Expressing error margins, experimental results, and efficiency rates often involves percentages. In fields like chemistry, expressing concentrations of solutions as percentages is common practice.
-
Everyday Life: We encounter percentages daily. Understanding tip calculations in restaurants, interpreting nutritional information on food labels, or comprehending discounts in stores all require using percentage calculations.
Historical Significance of Percentages
The use of percentages can be traced back to ancient civilizations, although the modern notation using the "%" symbol didn't emerge until much later. Early forms of percentage calculations were used in ancient Rome, where taxes were often levied as a fraction of the assessed value of property. The widespread use of percentages became more prominent during the Middle Ages and Renaissance as commerce and trade expanded. The modern notation and widespread use of percentages became standardized during the 17th and 18th centuries.
Advanced Percentage Calculations: Beyond the Basics
While calculating 70% of 15 is straightforward, more complex percentage problems require a deeper understanding of the concepts. These can include:
-
Calculating percentage increase or decrease: Determining the percentage change between two values requires understanding the formula for percentage change: [(New Value - Old Value) / Old Value] * 100.
-
Finding the original value given a percentage and the resulting value: This often involves working backward from the result to find the original amount. For example, if a discounted price is $10.50 after a 30% discount, the original price can be calculated using algebra.
-
Compound percentages: This involves calculating percentages on percentages, which is particularly relevant in financial calculations involving compound interest.
-
Percentage points: It's crucial to distinguish between percentage points and percentage change. A change from 10% to 20% is a 10 percentage point increase, but a 100% percentage increase.
Conclusion: The Power of Percentage Calculations
In conclusion, while the answer to "What is 70 percent of 15?" is simply 10.5, the significance of percentage calculations extends far beyond this simple problem. Understanding percentages is a fundamental skill with widespread applications in various fields. From basic financial transactions to advanced statistical analysis, mastering percentage calculations empowers you to interpret data effectively, make informed decisions, and navigate the complexities of the modern world. This comprehensive understanding of percentages, coupled with the ability to calculate them accurately and efficiently, is a valuable asset in both personal and professional life. The ability to use various methods to arrive at the answer adds to the robustness of your understanding and allows for flexibility in tackling different problems. Remember, the simple question of finding 70% of 15 serves as a gateway to a much larger and more significant concept.
Latest Posts
Latest Posts
-
What Is 0 3333 As A Fraction
Apr 26, 2025
-
What Does An Open Circle On A Number Line Mean
Apr 26, 2025
-
7 8 Is How Many Inches
Apr 26, 2025
-
What Percent Is 11 Out Of 18
Apr 26, 2025
-
How Many Centimeters In 50 Meters
Apr 26, 2025
Related Post
Thank you for visiting our website which covers about What Is 70 Percent Of 15 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.