What Is 75 Percent Of 12
Kalali
Apr 09, 2025 · 5 min read
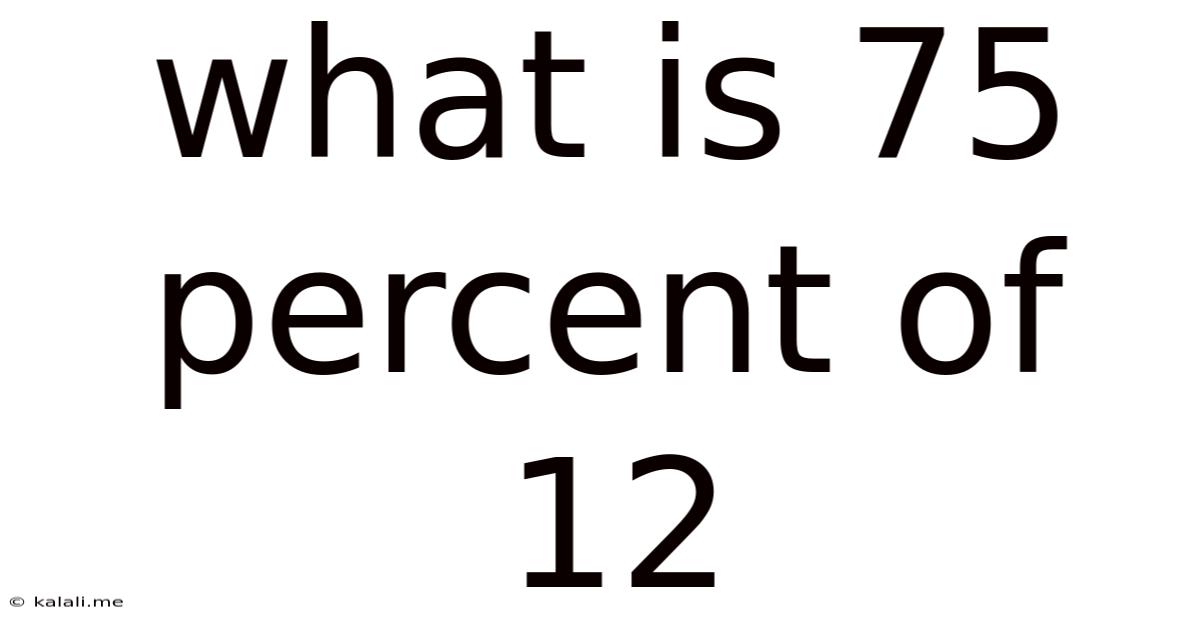
Table of Contents
What is 75 Percent of 12? A Deep Dive into Percentages and Their Applications
What is 75 percent of 12? The answer, of course, is 9. But this seemingly simple question opens a door to a much broader understanding of percentages, their calculation methods, real-world applications, and even the underlying mathematical principles. This article will not only answer the initial question but will also explore the intricacies of percentage calculations, different approaches to solving them, and how this fundamental concept impacts various aspects of our daily lives.
Meta Description: Discover how to calculate 75% of 12 and delve into the world of percentages. This comprehensive guide explores various methods, real-world applications, and the underlying mathematical concepts.
This seemingly straightforward calculation—finding 75% of 12—underpins many complex financial, scientific, and everyday scenarios. Understanding how to perform this calculation efficiently and accurately is a crucial skill, applicable across numerous disciplines. We'll explore different approaches, from the most basic to more sophisticated methods, ensuring a comprehensive understanding of the subject.
Understanding Percentages: A Foundation
Before diving into the specifics of calculating 75% of 12, let's solidify our understanding of percentages. A percentage is simply a fraction expressed as a part of 100. The term "percent" literally means "out of one hundred" (per centum in Latin). Therefore, 75% can be written as the fraction 75/100 or the decimal 0.75. This representation is key to understanding how percentages are calculated.
Method 1: The Fraction Method
This is perhaps the most intuitive method, especially for those comfortable working with fractions. We convert the percentage into a fraction and then multiply it by the whole number.
- Convert the percentage to a fraction: 75% = 75/100.
- Simplify the fraction (optional): 75/100 can be simplified to 3/4 by dividing both the numerator and the denominator by 25.
- Multiply the fraction by the whole number: (3/4) * 12 = 36/4 = 9.
Therefore, 75% of 12 is 9. This method clearly illustrates the fundamental relationship between percentages, fractions, and whole numbers.
Method 2: The Decimal Method
This method utilizes the decimal equivalent of the percentage. It's often faster and preferred for those who are comfortable with decimal calculations.
- Convert the percentage to a decimal: 75% = 0.75 (divide the percentage by 100).
- Multiply the decimal by the whole number: 0.75 * 12 = 9.
This method directly translates the percentage into a easily manageable decimal, resulting in a straightforward calculation.
Method 3: The Proportion Method
The proportion method offers a slightly different perspective, leveraging the concept of ratios. It's particularly useful for understanding the relationship between the percentage, the part, and the whole.
We can set up a proportion:
- x / 12 = 75 / 100
Where 'x' represents 75% of 12. Solving for 'x':
- Cross-multiply: 100x = 75 * 12
- Simplify: 100x = 900
- Solve for x: x = 900 / 100 = 9
This method provides a more algebraic approach, highlighting the proportional relationship inherent in percentage calculations.
Real-World Applications: Where Percentages Matter
Understanding percentage calculations isn't just about academic exercises; it's a crucial skill with widespread practical applications. Let's explore some examples:
-
Sales and Discounts: Retail stores frequently advertise discounts as percentages. For example, a 25% discount on a $40 item means you save 25% of $40, which is $10, making the final price $30.
-
Finance and Investments: Interest rates on loans and savings accounts are typically expressed as percentages. Calculating interest earned or paid requires understanding percentage calculations. For instance, a 5% interest rate on a $1000 investment means you earn $50 in interest in one year.
-
Taxes and Tipping: Sales taxes and restaurant tips are also calculated as percentages of the total amount. Understanding these percentages allows you to accurately determine the final cost or the appropriate tip amount.
-
Statistics and Data Analysis: Percentages are fundamental in presenting and interpreting statistical data. For instance, expressing survey results as percentages provides a clearer and more easily understood representation of the data. Understanding the percentage of respondents who favored a particular option is critical to data analysis.
-
Science and Engineering: Percentages are used in various scientific and engineering applications, such as expressing the concentration of a solution, measuring efficiency of a process or device, or even calculating error margins in experimental data.
-
Everyday Life: From calculating the percentage of your daily calorie intake to determining the percentage of your monthly budget allocated to different expenses, percentages are woven into the fabric of our daily lives.
Advanced Percentage Calculations: Beyond the Basics
While calculating 75% of 12 is relatively straightforward, the concept of percentages extends to more complex scenarios. Let's consider some examples:
-
Finding the Percentage Increase or Decrease: This involves calculating the percentage change between two values. The formula is: [(New Value - Old Value) / Old Value] * 100. For example, if a stock price rises from $10 to $12, the percentage increase is [(12 - 10) / 10] * 100 = 20%.
-
Calculating Percentage Points: Percentage points refer to the arithmetic difference between two percentages. For instance, if the unemployment rate rises from 5% to 8%, the increase is 3 percentage points, not 3%.
-
Working with Compound Percentages: Compound interest, where interest is calculated on both the principal and accumulated interest, involves multiple percentage calculations. Understanding compound growth is crucial in long-term financial planning.
-
Solving for the Original Value: If you know the percentage and the resulting value, you can work backwards to find the original value. For example, if 20% of a number is 4, the original number is 4 / (20/100) = 20.
Conclusion: Mastering Percentages for a Better Understanding of the World
The seemingly simple question "What is 75 percent of 12?" unveils a vast and crucial mathematical concept. Understanding percentages and their calculations is essential for navigating a wide range of situations, from personal finance and shopping to professional contexts and scientific endeavors. By mastering various methods of calculating percentages and appreciating their diverse applications, we equip ourselves with a valuable skillset that enhances our understanding and ability to interpret the world around us. The ability to quickly and accurately calculate percentages is a skill that will undoubtedly benefit you in countless ways throughout your life. Remember the fundamental principles—percentages are simply fractions of 100—and practice different calculation methods to solidify your understanding. With practice, these calculations will become second nature, empowering you to confidently tackle increasingly complex percentage-related problems.
Latest Posts
Latest Posts
-
13 6 As A Mixed Number
Apr 18, 2025
-
What Is 3 Percent Of 200
Apr 18, 2025
-
How To Solve A Log Without A Calculator
Apr 18, 2025
-
What Is 10 Degrees Celsius On The Fahrenheit Scale
Apr 18, 2025
-
How Much Is 187 Ml In Ounces
Apr 18, 2025
Related Post
Thank you for visiting our website which covers about What Is 75 Percent Of 12 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.