What Is 75 Percent Of 200
Kalali
Apr 04, 2025 · 5 min read
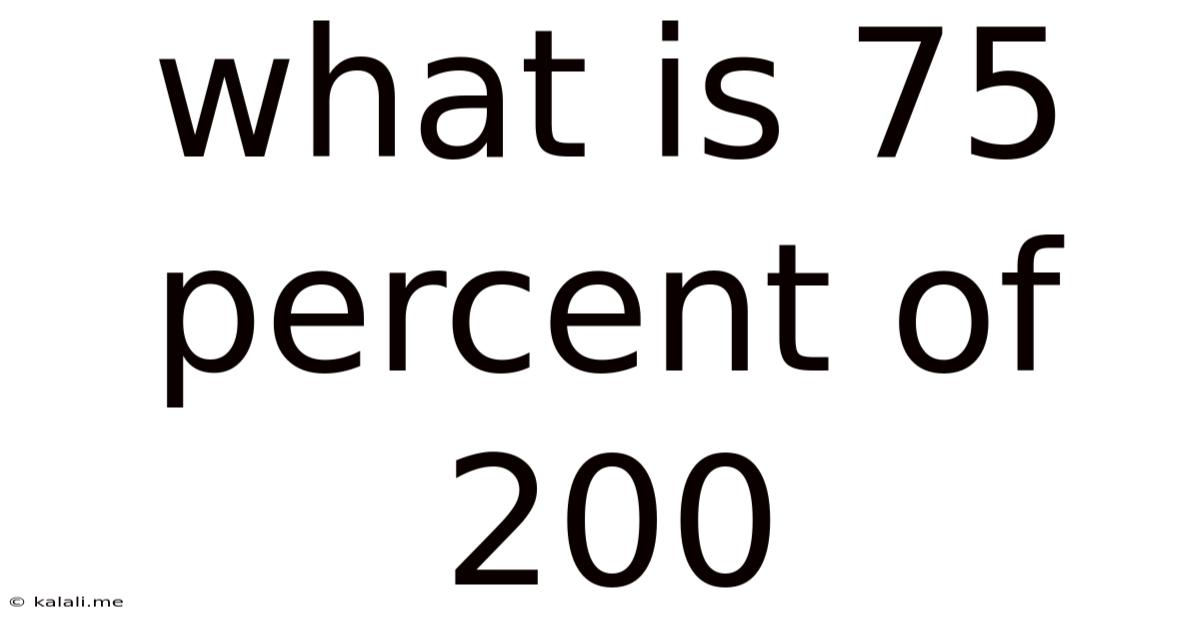
Table of Contents
What is 75 Percent of 200? A Deep Dive into Percentages and Their Applications
Finding 75% of 200 might seem like a simple arithmetic problem, but it opens the door to understanding a fundamental concept in mathematics and its widespread applications in various fields. This article will not only answer the question directly but also explore the broader context of percentages, providing you with the tools and knowledge to tackle similar calculations with confidence. We'll delve into different methods for calculating percentages, discuss real-world applications, and even touch upon advanced percentage-related concepts.
Understanding Percentages: The Basics
A percentage is simply a fraction expressed as a part of 100. The term "percent" literally means "per hundred." So, 75% means 75 out of 100, or 75/100. This fraction can be simplified to 3/4. This simple representation is key to understanding how percentages work. We use percentages to express proportions, ratios, and changes in a way that's easily understandable and comparable.
Key Terminology:
- Percentage: A proportion or rate expressed as a fraction of 100.
- Base Value: The total value or the number you're finding a percentage of. In our example, 200 is the base value.
- Percentage Value: The result of the percentage calculation. This is what we're trying to find—75% of 200.
- Rate: The percentage itself (in this case, 75%).
Calculating 75% of 200: Three Methods
There are several ways to calculate 75% of 200. Let's explore three common approaches:
Method 1: Using the Fraction Equivalent
As mentioned earlier, 75% is equivalent to the fraction 3/4. Therefore, finding 75% of 200 is the same as finding 3/4 of 200.
- Multiply the fraction by the base value: (3/4) * 200 = 600/4
- Simplify the fraction: 600/4 = 150
Therefore, 75% of 200 is 150.
Method 2: Converting Percentage to Decimal
Another approach involves converting the percentage to a decimal. To do this, divide the percentage by 100. 75% divided by 100 is 0.75.
- Convert the percentage to a decimal: 75% = 0.75
- Multiply the decimal by the base value: 0.75 * 200 = 150
Again, we arrive at the answer: 75% of 200 is 150.
Method 3: Using Proportions
This method uses the concept of proportions to solve for the unknown percentage value. We can set up a proportion as follows:
75/100 = x/200
Where 'x' represents the value we're trying to find (75% of 200). To solve for x, we can cross-multiply:
75 * 200 = 100 * x
15000 = 100x
x = 15000 / 100
x = 150
So, once again, 75% of 200 is 150.
Real-World Applications of Percentage Calculations
Understanding percentage calculations is crucial in various aspects of daily life and professional settings. Here are a few examples:
1. Retail Discounts:
Imagine a store offering a 75% discount on an item originally priced at $200. Using the methods above, we know the discount amount is $150, making the final price $50. This is a common scenario where percentage calculations are essential for determining sale prices.
2. Financial Calculations:
Percentage calculations are fundamental in finance. Calculating interest rates on loans or investments, understanding tax rates, and analyzing financial statements all involve percentage computations. For example, a 75% loan-to-value ratio means a loan amount is 75% of the property's value.
3. Data Analysis and Statistics:
Percentages are vital for representing data in a clear and concise manner. For instance, if a survey shows that 75% of respondents prefer a particular product, it offers a quick and easily understandable summary of the results. This is frequently used in market research, scientific studies, and public opinion polls.
4. Scientific and Engineering Applications:
Percentage calculations are also common in various scientific and engineering fields. They are used to express efficiency, error margins, concentration levels, and many other crucial parameters.
5. Everyday Life:
Even in everyday life, understanding percentages helps us make informed decisions. Calculating tips in restaurants, determining the amount saved on sales, or understanding nutritional information on food labels all involve percentage calculations.
Advanced Percentage Concepts
While calculating 75% of 200 is relatively straightforward, there are more complex percentage-related concepts that build upon this foundation:
1. Percentage Increase and Decrease:
This involves calculating the change in a value as a percentage. For example, if a value increases from 200 to 250, the percentage increase is calculated as follows:
(Increase/Original Value) * 100% = ((250-200)/200) * 100% = 25%
Similarly, a percentage decrease can be calculated.
2. Compound Interest:
This is a crucial concept in finance where interest earned is added to the principal, and subsequent interest calculations are based on the accumulated amount. Understanding compound interest involves repeated percentage calculations over time.
3. Percentage Points:
It's important to distinguish between percentage points and percentage change. For example, an increase from 25% to 30% is a 5-percentage point increase, but a percentage increase of approximately 20% ( (5/25) * 100% ).
Mastering Percentages: Tips and Practice
To become proficient in percentage calculations, consistent practice is key. Here are some helpful tips:
- Memorize common percentage equivalents: Knowing that 25% = 1/4, 50% = 1/2, and 75% = 3/4 can greatly simplify calculations.
- Practice different methods: Become comfortable using different approaches, such as the fraction, decimal, and proportion methods.
- Use online calculators and resources: While it's important to understand the underlying principles, online calculators can be helpful for double-checking your work and exploring more complex scenarios.
- Relate percentages to real-world problems: By applying percentage calculations to practical situations, you'll improve your understanding and retain the information more effectively.
Conclusion: The Power of Percentages
The seemingly simple question, "What is 75% of 200?" serves as a gateway to a vast world of mathematical applications. Mastering percentage calculations is a valuable skill applicable across various disciplines, from everyday financial decisions to complex scientific and engineering analyses. By understanding the fundamental principles and practicing different methods, you can confidently tackle any percentage-related problem. Remember, the power of percentages lies not only in their ability to provide precise numerical results but also in their ability to clearly communicate proportions, ratios, and changes in a way that’s easily understood by all.
Latest Posts
Latest Posts
-
What Percentage Is 3 Of 16
Apr 12, 2025
-
What Is 3 And 1 2 As A Decimal
Apr 12, 2025
-
How Many Centimeters In 25 Meters
Apr 12, 2025
-
What Is The Least Common Multiple Of 8 And 2
Apr 12, 2025
-
How Many Feet Is 41 In
Apr 12, 2025
Related Post
Thank you for visiting our website which covers about What Is 75 Percent Of 200 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.