What Is 8/20 As A Percent
Kalali
Apr 11, 2025 · 5 min read
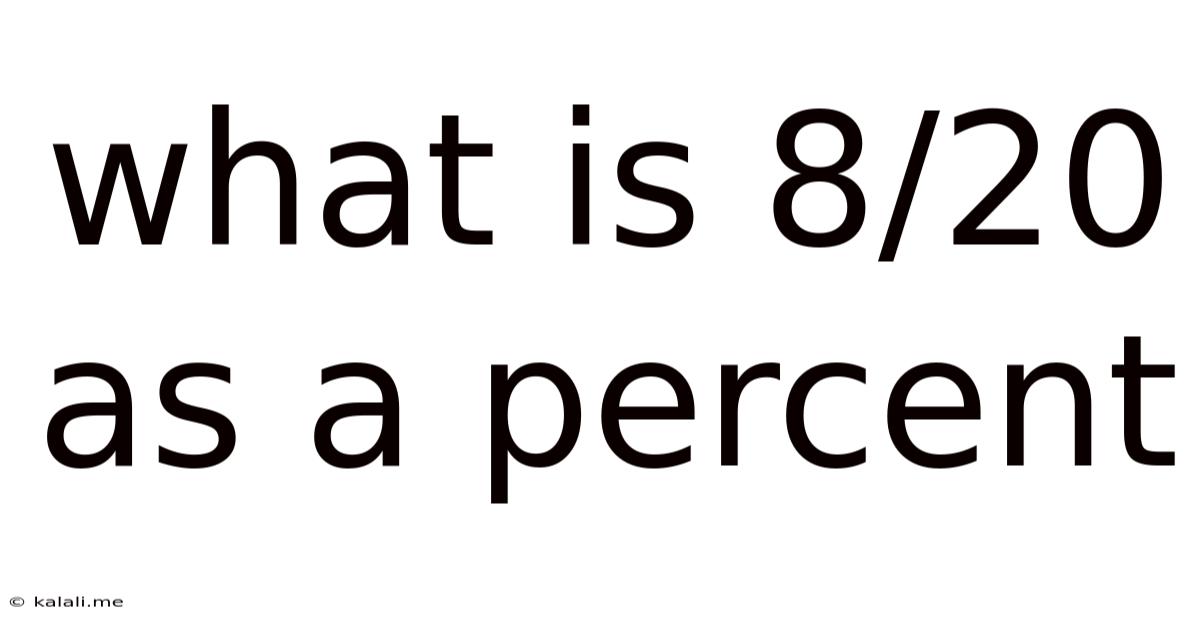
Table of Contents
What is 8/20 as a Percent? A Comprehensive Guide to Fraction-to-Percentage Conversion
Understanding how to convert fractions to percentages is a fundamental skill in mathematics with widespread applications in various fields, from finance and statistics to everyday life. This comprehensive guide will not only answer the question "What is 8/20 as a percent?" but will also delve into the underlying principles and provide you with the tools to confidently tackle similar conversions. We'll explore multiple methods, ensuring you grasp the concept thoroughly and can apply it to any fraction. This guide is designed to be beginner-friendly while also offering insights for those seeking a deeper understanding.
Meta Description: Learn how to convert fractions to percentages. This comprehensive guide explains how to calculate 8/20 as a percent, detailing multiple methods and providing valuable insights into fraction-to-percentage conversion.
Understanding Fractions and Percentages
Before diving into the specific calculation of 8/20, let's refresh our understanding of fractions and percentages.
A fraction represents a part of a whole. It's expressed as a ratio of two numbers: the numerator (the top number) and the denominator (the bottom number). The numerator indicates the number of parts we have, while the denominator indicates the total number of parts in the whole.
A percentage, denoted by the symbol %, represents a fraction out of 100. It expresses a proportion relative to a whole, where the whole is always considered as 100 units. For instance, 50% means 50 out of 100, or 50/100.
Method 1: Simplifying the Fraction
The simplest method for converting 8/20 to a percentage involves simplifying the fraction before converting it to a decimal and then a percentage.
-
Simplify the Fraction: Notice that both the numerator (8) and the denominator (20) are divisible by 4. Dividing both by 4, we get:
8 ÷ 4 = 2 20 ÷ 4 = 5
Therefore, 8/20 simplifies to 2/5.
-
Convert to a Decimal: To convert the simplified fraction 2/5 to a decimal, divide the numerator (2) by the denominator (5):
2 ÷ 5 = 0.4
-
Convert to a Percentage: To convert the decimal 0.4 to a percentage, multiply it by 100:
0.4 x 100 = 40%
Therefore, 8/20 is equal to 40%.
Method 2: Direct Conversion to Decimal
This method involves directly converting the fraction to a decimal and then to a percentage without simplifying the fraction first.
-
Convert to a Decimal: Divide the numerator (8) by the denominator (20):
8 ÷ 20 = 0.4
-
Convert to a Percentage: Multiply the decimal 0.4 by 100:
0.4 x 100 = 40%
This method yields the same result: 8/20 is equal to 40%.
Method 3: Using Proportions
This method utilizes the concept of proportions to solve the problem. We can set up a proportion to find the equivalent percentage:
8/20 = x/100
Where 'x' represents the percentage we want to find. To solve for 'x', cross-multiply:
20x = 800
Divide both sides by 20:
x = 800 ÷ 20 = 40
Therefore, x = 40, meaning 8/20 is equal to 40%.
Understanding the Concept of Proportionality
The core concept behind these methods is proportionality. A percentage is simply a fraction expressed as a proportion of 100. By manipulating the fraction or using proportions, we effectively scale the fraction to represent its equivalent value out of 100. This principle extends to all fraction-to-percentage conversions.
Practical Applications of Fraction-to-Percentage Conversion
The ability to convert fractions to percentages is crucial in numerous real-world scenarios:
- Finance: Calculating interest rates, discounts, profit margins, and tax rates.
- Statistics: Representing data in charts and graphs, calculating probabilities, and interpreting statistical analyses.
- Everyday Life: Determining tips in restaurants, calculating sale prices, understanding survey results, and comparing different proportions.
Beyond 8/20: Applying the Techniques to Other Fractions
The methods described above can be applied to any fraction. Let's illustrate with a few examples:
-
Converting 3/4 to a percentage:
- Convert to decimal: 3 ÷ 4 = 0.75
- Convert to percentage: 0.75 x 100 = 75%
-
Converting 1/8 to a percentage:
- Convert to decimal: 1 ÷ 8 = 0.125
- Convert to percentage: 0.125 x 100 = 12.5%
-
Converting 5/6 to a percentage:
- Convert to decimal: 5 ÷ 6 ≈ 0.8333
- Convert to percentage: 0.8333 x 100 ≈ 83.33%
Handling Decimals in Fractions
Some fractions might result in recurring decimals when converted. In such cases, it's common practice to round the percentage to a reasonable number of decimal places, depending on the context and required level of precision.
Using Calculators for Fraction-to-Percentage Conversion
While manual calculations are valuable for understanding the underlying principles, calculators can simplify the process, especially for more complex fractions. Most calculators have a function to directly convert fractions to decimals and then to percentages.
Advanced Techniques: Using Algebra
For more complex scenarios involving multiple fractions or algebraic expressions, algebraic techniques can be employed. These techniques involve setting up equations and solving for the unknown variable representing the percentage.
Conclusion
Converting fractions to percentages is a fundamental mathematical skill with far-reaching applications. This guide has comprehensively demonstrated how to calculate 8/20 as a percent (40%), outlining multiple methods and providing practical examples. By mastering these techniques, you'll be well-equipped to handle fraction-to-percentage conversions in various contexts, from simple everyday calculations to more complex mathematical problems. Remember to practice regularly to reinforce your understanding and build confidence in your abilities. The ability to convert fractions to percentages efficiently and accurately is a valuable asset in many areas of life and study.
Latest Posts
Latest Posts
-
How Many Bottles Is 64 Oz Of Water
Jul 02, 2025
-
How Many Ounces In Pound Of Meat
Jul 02, 2025
-
What Is The Diameter Of A Quarter
Jul 02, 2025
-
Spoon Gets Hot In A Bowl Of Soup
Jul 02, 2025
-
How Many Cups In A 16 Oz Sour Cream
Jul 02, 2025
Related Post
Thank you for visiting our website which covers about What Is 8/20 As A Percent . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.