What Is Bigger 2 3 Or 1 2
Kalali
Jul 31, 2025 · 5 min read
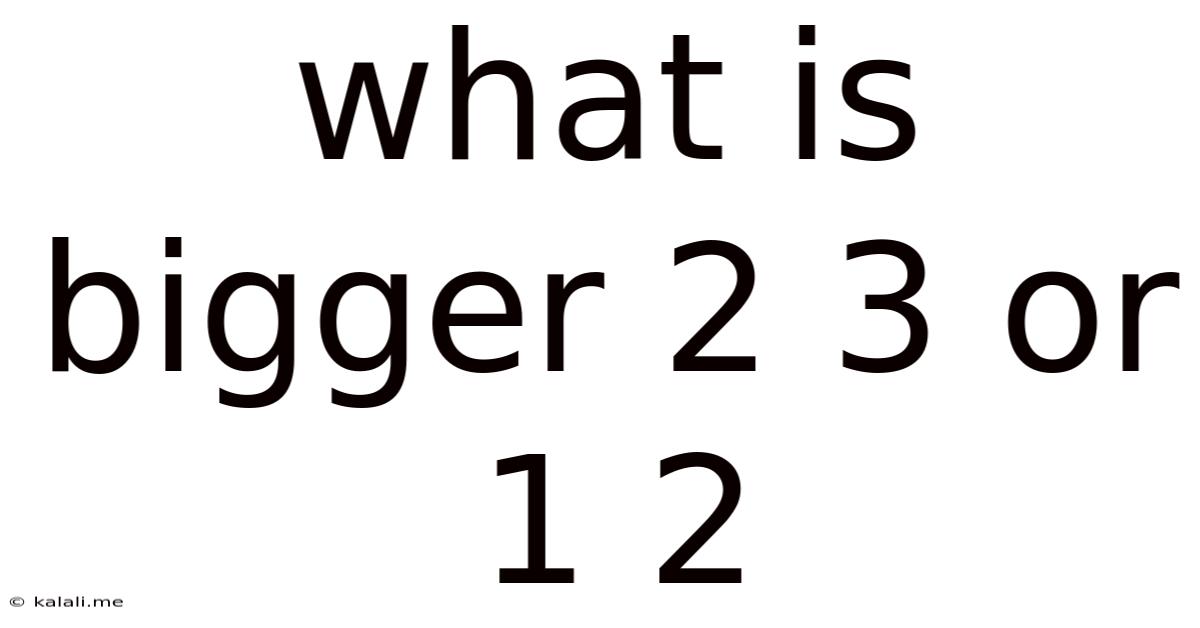
Table of Contents
What's Bigger: 2/3 or 1/2? A Deep Dive into Fraction Comparison
This seemingly simple question – "What's bigger, 2/3 or 1/2?" – opens the door to a fascinating exploration of fractions, their representation, and various methods for comparing them. Understanding how to compare fractions is a fundamental skill in mathematics, crucial not just for academic success but also for everyday practical applications. This article will delve into several approaches to solve this problem and illuminate the underlying mathematical concepts. We'll explore visual methods, equivalent fractions, decimal conversions, and even consider the broader implications of fractional comparison in real-world scenarios.
Understanding Fractions: A Quick Recap
Before we tackle the comparison, let's refresh our understanding of fractions. A fraction represents a part of a whole. It consists of two numbers: the numerator (the top number) and the denominator (the bottom number). The numerator indicates how many parts we have, while the denominator indicates how many equal parts the whole is divided into. In our case, we are comparing 2/3 and 1/2. 2/3 means we have 2 parts out of a total of 3 equal parts, while 1/2 means we have 1 part out of a total of 2 equal parts.
Method 1: Visual Representation
One of the most intuitive ways to compare fractions is through visual representation. Imagine two identical circles.
- For 1/2: Divide the first circle into two equal halves. Shade one half.
- For 2/3: Divide the second circle into three equal thirds. Shade two thirds.
By visually comparing the shaded areas, it becomes clear that the shaded portion of the circle representing 2/3 is larger than the shaded portion representing 1/2. This visual method offers a clear, intuitive understanding, particularly helpful for beginners grasping the concept of fractions. This method works best for simpler fractions; for more complex fractions, other methods become more efficient.
Method 2: Finding a Common Denominator
A more robust method for comparing fractions involves finding a common denominator. This means finding a number that is a multiple of both denominators (3 and 2 in this case). The least common multiple (LCM) of 3 and 2 is 6.
- Convert 1/2: To get a denominator of 6, we multiply both the numerator and the denominator by 3: (1 x 3) / (2 x 3) = 3/6
- Convert 2/3: To get a denominator of 6, we multiply both the numerator and the denominator by 2: (2 x 2) / (3 x 2) = 4/6
Now we have 3/6 and 4/6. Since both fractions have the same denominator, we can simply compare the numerators. 4 is greater than 3, therefore, 4/6 (which is equivalent to 2/3) is greater than 3/6 (which is equivalent to 1/2).
Method 3: Converting to Decimals
Another effective method is converting the fractions to decimals. This involves dividing the numerator by the denominator.
- 2/3: 2 ÷ 3 ≈ 0.6667
- 1/2: 1 ÷ 2 = 0.5
Comparing the decimal equivalents, 0.6667 is clearly greater than 0.5. Therefore, 2/3 is larger than 1/2. This method is particularly useful when dealing with fractions that are difficult to visualize or find a common denominator for quickly. However, it's important to remember that some fractions, like 2/3, result in repeating decimals, requiring rounding for practical comparisons.
Method 4: Cross-Multiplication
Cross-multiplication provides a quick and efficient way to compare two fractions. This method involves multiplying the numerator of the first fraction by the denominator of the second fraction and vice versa. Then, compare the resulting products.
- 2/3 and 1/2:
- Multiply 2 (numerator of 2/3) by 2 (denominator of 1/2): 2 x 2 = 4
- Multiply 3 (denominator of 2/3) by 1 (numerator of 1/2): 3 x 1 = 3
Since 4 > 3, the fraction 2/3 is greater than 1/2. This method elegantly avoids the need to find a common denominator, making it a concise and efficient comparison technique.
Real-World Applications of Fraction Comparison
The ability to compare fractions isn't just confined to the classroom. It has numerous practical applications in everyday life:
-
Cooking and Baking: Recipes often require precise measurements involving fractions. Understanding which fraction is larger ensures accurate ingredient proportions. For instance, determining whether you need 1/2 cup or 2/3 cup of sugar for a recipe relies on this fundamental skill.
-
Construction and Engineering: Precise measurements are crucial in construction and engineering projects. Comparing fractions ensures accurate calculations for dimensions, materials, and proportions. For example, determining whether a 2/3 inch pipe is larger than a 1/2 inch pipe is vital for ensuring proper fit and functionality.
-
Finance and Budgeting: Fractions are frequently used in financial calculations, such as determining percentages, interest rates, and proportions of budgets. Comparing fractions is essential for making informed financial decisions. For instance, deciding whether to invest in a bond offering a 2/3% return or a 1/2% return requires accurate fractional comparison.
-
Data Analysis: In many fields, data is presented using fractions or percentages. Comparing these values accurately allows for data interpretation and meaningful conclusions. For example, understanding the performance difference between two products with 2/3 and 1/2 customer satisfaction rates is crucial for business strategy.
Beyond 2/3 and 1/2: Extending the Concepts
The principles discussed here extend far beyond comparing just 2/3 and 1/2. The methods – visual representation, common denominators, decimal conversion, and cross-multiplication – are applicable to comparing any two fractions, regardless of their complexity. Mastering these techniques provides a solid foundation for tackling more advanced mathematical concepts involving fractions, ratios, and proportions. Understanding the underlying principles allows for accurate and efficient calculations in various contexts.
Conclusion: Mastering Fraction Comparison
The seemingly simple question of whether 2/3 or 1/2 is larger reveals a rich tapestry of mathematical concepts and practical applications. Through visual representation, finding common denominators, decimal conversion, and cross-multiplication, we've explored various methods to solve this problem. Understanding these methods and their underlying principles empowers us to confidently compare fractions in diverse situations, extending beyond academic exercises to real-world scenarios across various fields. The ability to compare fractions accurately is a fundamental skill that unlocks deeper understanding and efficient problem-solving in mathematics and beyond. It's a key building block for tackling more complex mathematical concepts and applications in the real world.
Latest Posts
Latest Posts
-
How Many Minutes Are In 360 Seconds
Aug 03, 2025
-
How To Calculate Square Feet Into Linear Feet
Aug 03, 2025
-
What Is A 56 Out Of 60
Aug 03, 2025
-
How Long Does Brandy Melville Take To Ship
Aug 03, 2025
-
Which Element Is More Likely To Become A Anion
Aug 03, 2025
Related Post
Thank you for visiting our website which covers about What Is Bigger 2 3 Or 1 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.