What Is Bigger 5 8 Or 1 2
Kalali
Jul 15, 2025 · 4 min read
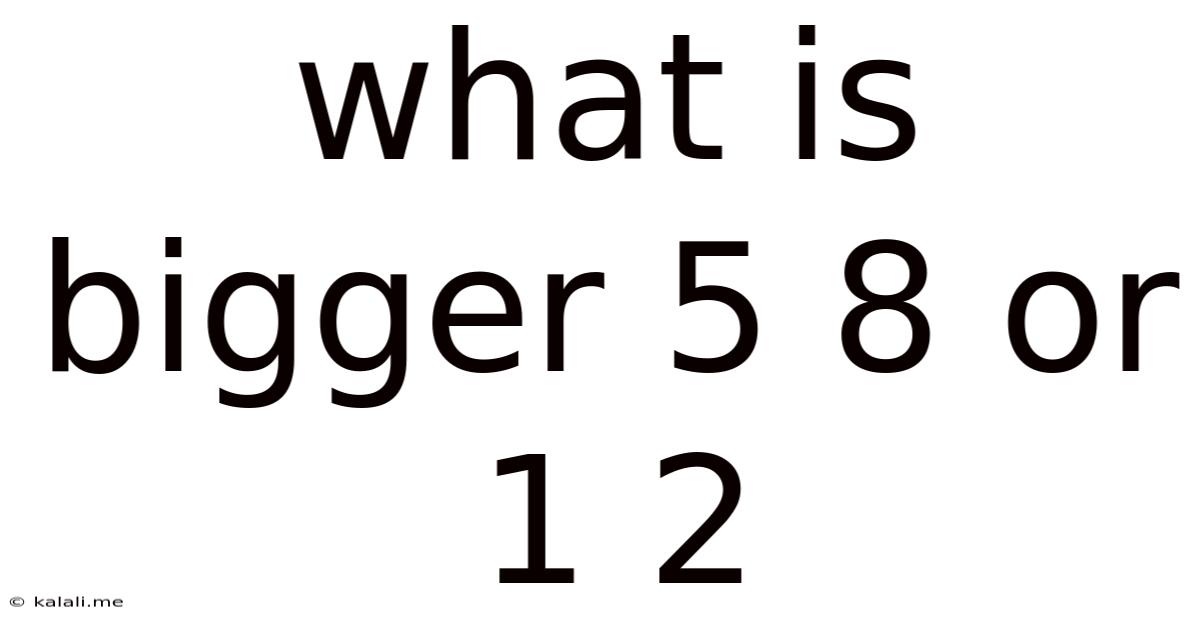
Table of Contents
What's Bigger: 5/8 or 1/2? A Deep Dive into Fraction Comparison
This seemingly simple question – "What's bigger: 5/8 or 1/2?" – can actually unlock a deeper understanding of fractions and their manipulation. While the answer might seem immediately obvious to some, exploring the various methods of comparison offers valuable insights into mathematical reasoning and problem-solving skills. This article will delve into multiple approaches to determine which fraction is larger, 5/8 or 1/2, and will also explore broader concepts related to fraction comparison and their applications. Understanding these concepts is crucial not only for mathematical proficiency but also for everyday problem-solving and even more advanced mathematical concepts.
Understanding Fractions: A Quick Recap
Before we embark on the comparison, let's refresh our understanding of fractions. A fraction represents a part of a whole. It's composed of two main parts:
- Numerator: The top number, indicating the number of parts we have.
- Denominator: The bottom number, indicating the total number of equal parts the whole is divided into.
For example, in the fraction 5/8, the numerator is 5 (we have 5 parts), and the denominator is 8 (the whole is divided into 8 equal parts).
Method 1: Finding a Common Denominator
This is arguably the most straightforward method for comparing fractions. The goal is to rewrite both fractions so they share the same denominator. This allows for a direct comparison of the numerators.
To find a common denominator for 5/8 and 1/2, we need to find the least common multiple (LCM) of 8 and 2. The LCM is 8.
- We don't need to change 5/8, as its denominator is already 8.
- To convert 1/2 to a fraction with a denominator of 8, we multiply both the numerator and the denominator by 4: (1 x 4) / (2 x 4) = 4/8
Now we can compare 5/8 and 4/8. Since 5 > 4, we conclude that 5/8 is bigger than 1/2.
Method 2: Converting to Decimals
Another effective method involves converting both fractions into decimals. This allows for a simple numerical comparison.
- To convert 5/8 to a decimal, we divide the numerator by the denominator: 5 ÷ 8 = 0.625
- To convert 1/2 to a decimal, we divide the numerator by the denominator: 1 ÷ 2 = 0.5
Comparing the decimals, 0.625 > 0.5, confirming that 5/8 is bigger than 1/2. This method is particularly useful when dealing with more complex fractions where finding a common denominator might be challenging.
Method 3: Visual Representation
Visual aids can be extremely helpful, especially when explaining fractions to beginners. Imagine a pizza cut into 8 equal slices.
- 5/8 represents 5 slices out of the 8 total slices.
- 1/2 represents half the pizza, which is equivalent to 4 slices (8 slices / 2 = 4 slices).
By visualizing this, it's clear that 5 slices (5/8) are more than 4 slices (1/2), once again demonstrating that 5/8 is greater than 1/2. This method is excellent for building intuitive understanding.
Method 4: Using a Number Line
A number line provides a visual representation of the relative positions of fractions. Plotting both 5/8 and 1/2 on a number line clearly shows that 5/8 lies to the right of 1/2, indicating that 5/8 is greater. This method reinforces the concept of magnitude and ordering of fractions.
Beyond the Basic Comparison: Exploring Related Concepts
The comparison of 5/8 and 1/2 serves as a springboard for understanding more advanced concepts within the realm of fractions:
Equivalent Fractions:
Equivalent fractions represent the same value but have different numerators and denominators. For example, 1/2, 2/4, 4/8, and 8/16 are all equivalent fractions. Understanding equivalent fractions is crucial for simplifying fractions and finding common denominators.
Improper Fractions and Mixed Numbers:
An improper fraction has a numerator that is larger than or equal to its denominator (e.g., 5/4). A mixed number combines a whole number and a fraction (e.g., 1 ¼). Converting between improper fractions and mixed numbers is a fundamental skill in fraction manipulation.
Fraction Operations:
Adding, subtracting, multiplying, and dividing fractions require a solid understanding of the underlying principles. These operations are essential for solving more complex problems involving fractions.
Applications of Fractions in Real Life:
Fractions are used extensively in everyday life, from cooking and baking to measuring ingredients and calculating proportions. They are also crucial in many fields, including engineering, finance, and computer science. Understanding fraction comparison directly translates to real-world scenarios such as determining which deal offers a better discount or deciding between different package sizes.
Conclusion:
The seemingly simple question of whether 5/8 or 1/2 is bigger offers a rich opportunity to explore fundamental concepts in mathematics. By employing various methods – finding a common denominator, converting to decimals, using visual representations, or employing a number line – we can confidently determine that 5/8 is greater than 1/2. Furthermore, understanding the underlying principles of fraction comparison lays the groundwork for mastering more advanced mathematical concepts and applying these skills effectively in various aspects of life. Remember, a deep understanding of fractions is not merely an academic pursuit; it's a practical tool with far-reaching applications in the real world.
Latest Posts
Latest Posts
-
How Much Does 5 Gallons Of Sand Weigh
Jul 15, 2025
-
How Many Hours Are In 4 Months
Jul 15, 2025
-
Gifts That Start With The Letter V
Jul 15, 2025
-
How Many Copper Pennies To A Pound
Jul 15, 2025
-
How Many Cups Of Sour Cream In A Pound
Jul 15, 2025
Related Post
Thank you for visiting our website which covers about What Is Bigger 5 8 Or 1 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.