What Is Diameter Of A Cylinder
Kalali
Apr 01, 2025 · 6 min read
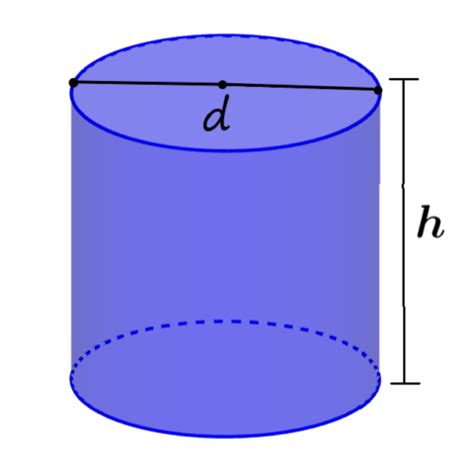
Table of Contents
What is the Diameter of a Cylinder? A Comprehensive Guide
The diameter of a cylinder is a fundamental concept in geometry and engineering, crucial for calculating volume, surface area, and various other properties. Understanding what it is and how to calculate it is essential in numerous fields, from designing engine components to calculating the capacity of storage tanks. This comprehensive guide will delve deep into the definition, calculation, real-world applications, and related concepts of the cylinder's diameter.
Defining the Diameter of a Cylinder
A cylinder is a three-dimensional geometric shape with two parallel circular bases connected by a curved surface. The diameter of a cylinder refers to the distance across the circular base, passing through the center. It's essentially the longest chord of the circle forming the base. Think of it as the distance you'd measure if you stretched a string across the widest part of the circular end of the cylinder.
Crucially, the cylinder's diameter is constant throughout its length. This means that no matter where you measure the diameter on the base, the value remains the same. This consistent diameter differentiates it from other three-dimensional shapes like cones or spheres, where measurements can vary depending on the point of measurement.
Distinguishing Diameter from Radius and Circumference
It's important to distinguish the diameter from two closely related concepts: the radius and the circumference.
-
Radius: The radius is half the diameter. It's the distance from the center of the circular base to any point on the circumference. The formula connecting radius (r) and diameter (d) is:
d = 2rorr = d/2. -
Circumference: The circumference is the distance around the circular base. It's calculated using the formula:
C = πdorC = 2πr, where π (pi) is approximately 3.14159.
Understanding these relationships is vital for accurate calculations involving cylinders.
Calculating the Diameter of a Cylinder
The method for determining the diameter of a cylinder depends on the information available.
1. When the Radius is Known:
The simplest scenario is when the radius of the cylinder's base is known. Using the formula mentioned earlier, the diameter (d) can be easily calculated:
d = 2r
For example, if the radius is 5 cm, the diameter is 2 * 5 cm = 10 cm.
2. When the Circumference is Known:
If the circumference (C) of the cylinder's base is known, the diameter can be calculated using the following formula:
d = C/π
This formula is derived by rearranging the circumference formula (C = πd). Remember to use a sufficiently accurate value for π (e.g., 3.14159 or the π button on your calculator) for precise results.
For instance, if the circumference is 30 cm, the diameter is approximately 30 cm / 3.14159 ≈ 9.55 cm.
3. When the Area of the Base is Known:
The area (A) of the circular base is related to the diameter by the formula:
A = π(d/2)² or A = πr²
To find the diameter, we need to rearrange this formula:
d = 2√(A/π)
If the area of the base is 78.54 cm², the diameter is approximately 2√(78.54 cm²/3.14159) ≈ 10 cm.
4. Measuring the Diameter Directly:
In many practical situations, the simplest way to find the diameter is to measure it directly using a ruler, caliper, or other appropriate measuring tool. This method is particularly useful when dealing with physical objects. Accuracy depends on the precision of the measuring instrument and the care taken during measurement.
Real-World Applications of Cylinder Diameter Calculations
Understanding and calculating the diameter of a cylinder has numerous real-world applications across various fields:
1. Engineering and Manufacturing:
- Engine design: Cylinder diameters are crucial in designing internal combustion engines. The diameter determines the engine's displacement and power output.
- Pipe sizing: In plumbing and pipefitting, the diameter dictates the flow rate of liquids or gases.
- Mechanical design: Cylinder diameters are fundamental in designing various mechanical components, such as pistons, hydraulic cylinders, and rollers.
- Manufacturing processes: Accurate diameter calculations are essential in manufacturing processes involving cylindrical components, ensuring proper fit and function.
2. Architecture and Construction:
- Column dimensions: In structural engineering, the diameter of cylindrical columns influences their load-bearing capacity.
- Pipe and conduit sizing: The diameter of pipes and conduits used in building services affects the flow of water, electricity, and other utilities.
- Tank design: The diameter of cylindrical tanks is crucial in determining their storage capacity.
3. Science and Research:
- Fluid dynamics: Cylinder diameter is a key parameter in studying fluid flow and pressure.
- Material science: Analyzing cylindrical specimens requires accurate diameter measurements for material property testing.
- Physics experiments: Numerous physics experiments utilize cylinders, and diameter measurements are essential for data analysis.
4. Everyday Life:
- Packaging: Many products are packaged in cylindrical containers, and the diameter is crucial for packaging design and storage.
- Food and beverage industry: The diameter of cylindrical cans and bottles is important for storage, transportation, and marketing.
- Household items: Many everyday items, such as candles, drinking glasses, and batteries, are cylindrical in shape, and their diameters are relevant for their usability and storage.
Advanced Concepts and Related Calculations
Beyond the basic diameter calculations, understanding certain related concepts can enhance your comprehension of cylindrical geometry:
1. Surface Area:
The surface area of a cylinder includes the areas of its two circular bases and its curved lateral surface. The formula for the total surface area (TSA) is:
TSA = 2πr² + 2πrh
where 'r' is the radius and 'h' is the height of the cylinder. Knowing the diameter allows you to easily calculate the radius and thus the surface area.
2. Volume:
The volume of a cylinder is the amount of space it occupies. It's calculated using the formula:
V = πr²h
Again, knowing the diameter helps in determining the radius and subsequently the volume.
3. Cross-sectional Area:
The cross-sectional area of a cylinder is the area of a section obtained by cutting it perpendicular to its axis. For a cylinder, this is simply the area of the circular base:
A = πr²
Conclusion: Mastering Cylinder Diameter Calculations
The diameter of a cylinder is a fundamental geometric property with widespread applications in numerous fields. Understanding its definition, calculation methods, and related concepts is crucial for anyone working with cylindrical shapes, whether in engineering, architecture, science, or everyday life. By mastering these calculations, you gain valuable skills applicable to various practical and theoretical problems involving cylinders. Accurate diameter measurement and calculation are vital for ensuring the functionality, safety, and efficiency of countless applications. Remember to choose the appropriate method depending on the available information, and always double-check your calculations for accuracy.
Latest Posts
Latest Posts
-
Bromine Readily Forms The Following Monatomic Ion
Apr 02, 2025
-
Cuanto Es 20 Libras En Kilos
Apr 02, 2025
-
The Shaft Of A Long Bone Is The
Apr 02, 2025
-
What Four Substances Are Recycled During Photosynthesis And Respiration
Apr 02, 2025
-
What Is 4 Inches In Millimeters
Apr 02, 2025
Related Post
Thank you for visiting our website which covers about What Is Diameter Of A Cylinder . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
