What Is Greater 1 2 Or 2 3
Kalali
Aug 22, 2025 · 5 min read
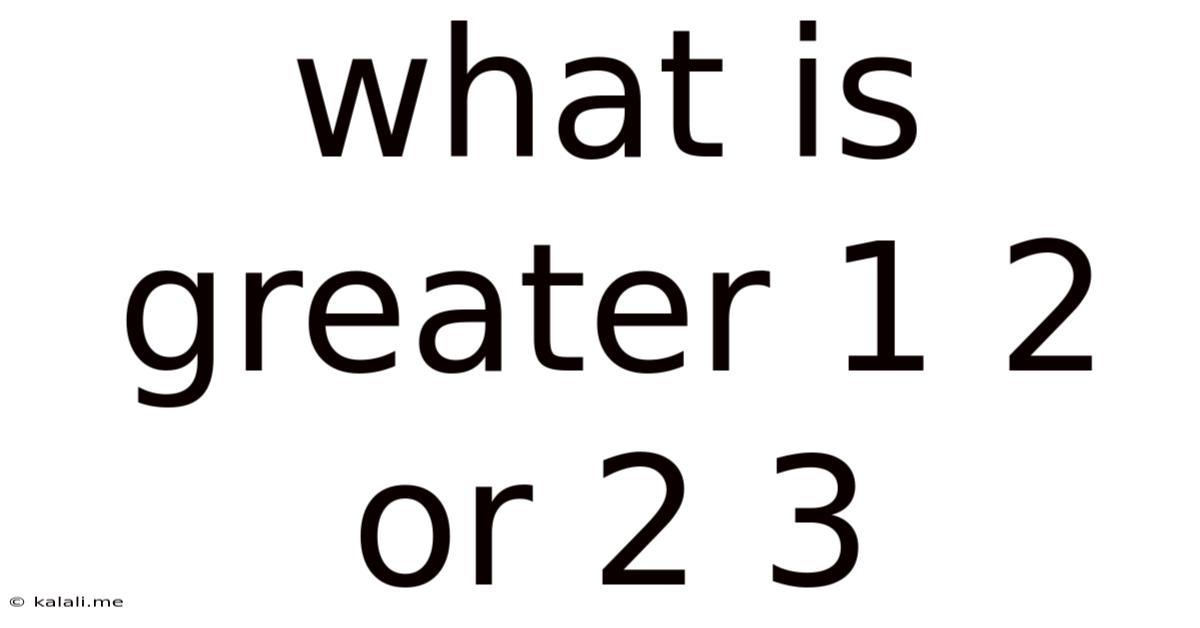
Table of Contents
What's Greater: 1/2 or 2/3? A Deep Dive into Fraction Comparison
This article will explore the seemingly simple question: which is greater, 1/2 or 2/3? While the answer might seem immediately obvious to some, a deeper dive reveals opportunities to solidify foundational mathematical understanding and explore various methods for comparing fractions. This exploration is beneficial not only for students but also for anyone looking to refresh their understanding of fractions and build stronger numerical reasoning skills. This will include methods applicable to more complex fraction comparisons.
Understanding Fractions: A Quick Refresher
Before we delve into comparing 1/2 and 2/3, let's briefly review the fundamental components of a fraction. A fraction represents a part of a whole. It's composed of two key elements:
- Numerator: The top number, indicating the number of parts we have.
- Denominator: The bottom number, indicating the total number of equal parts the whole is divided into.
For example, in the fraction 1/2, the numerator (1) represents one part, and the denominator (2) indicates the whole is divided into two equal parts.
Method 1: Finding a Common Denominator
The most common and perhaps most straightforward method for comparing fractions is finding a common denominator. This involves converting both fractions to equivalent fractions with the same denominator. We can then easily compare the numerators.
To find a common denominator for 1/2 and 2/3, we need to find a number that is a multiple of both 2 and 3. The least common multiple (LCM) of 2 and 3 is 6.
- Converting 1/2: To change the denominator from 2 to 6, we multiply both the numerator and the denominator by 3: (1 x 3) / (2 x 3) = 3/6
- Converting 2/3: To change the denominator from 3 to 6, we multiply both the numerator and the denominator by 2: (2 x 2) / (3 x 2) = 4/6
Now we have 3/6 and 4/6. Since both fractions have the same denominator, we can compare the numerators directly. 4 > 3, therefore, 2/3 > 1/2.
Method 2: Visual Representation
Visualizing fractions can be a highly effective method, especially for those who benefit from a more concrete approach to understanding mathematical concepts. We can represent 1/2 and 2/3 using diagrams, such as circles or rectangles, divided into equal parts.
Imagine two identical circles. Divide one circle into two equal halves and shade one half to represent 1/2. Divide the second circle into three equal parts and shade two of those parts to represent 2/3. By visually comparing the shaded areas, it becomes clear that the shaded area representing 2/3 is larger than the shaded area representing 1/2. This visual confirmation reinforces the conclusion that 2/3 > 1/2.
Method 3: Converting to Decimals
Another effective way to compare fractions is to convert them into decimal numbers. This method involves dividing the numerator by the denominator for each fraction.
- Converting 1/2 to a decimal: 1 ÷ 2 = 0.5
- Converting 2/3 to a decimal: 2 ÷ 3 ≈ 0.6667 (This is a repeating decimal)
Comparing the decimal equivalents, 0.6667 > 0.5, confirming that 2/3 > 1/2. This method is particularly helpful when dealing with more complex fractions or when needing to perform further calculations.
Method 4: Using Cross-Multiplication
Cross-multiplication offers a quick and efficient method for comparing two fractions. This method involves multiplying the numerator of one fraction by the denominator of the other and vice-versa. The fraction with the larger product is the greater fraction.
Let's compare 1/2 and 2/3 using cross-multiplication:
- Multiply the numerator of 1/2 (1) by the denominator of 2/3 (3): 1 x 3 = 3
- Multiply the numerator of 2/3 (2) by the denominator of 1/2 (2): 2 x 2 = 4
Since 4 > 3, the fraction 2/3 is greater than 1/2. Therefore, 2/3 > 1/2.
Extending the Concepts: Comparing More Complex Fractions
The methods discussed above are not limited to simple fractions like 1/2 and 2/3. They can be applied to more complex fractions, even those with larger numerators and denominators. For instance, let's consider comparing 5/8 and 7/12.
Using the common denominator method:
The LCM of 8 and 12 is 24.
- Converting 5/8: (5 x 3) / (8 x 3) = 15/24
- Converting 7/12: (7 x 2) / (12 x 2) = 14/24
Since 15 > 14, 5/8 > 7/12.
Using cross-multiplication:
- 5 x 12 = 60
- 7 x 8 = 56
Since 60 > 56, 5/8 > 7/12.
Practical Applications and Real-World Examples
The ability to compare fractions is a crucial skill with numerous practical applications in everyday life and various fields. Here are a few examples:
- Cooking and Baking: Recipes often involve fractional measurements of ingredients. Understanding fraction comparison is essential for accurately adjusting recipes or ensuring the correct proportions are used.
- Construction and Engineering: Precise measurements and calculations are critical in construction and engineering. Fractions are frequently used, and the ability to compare and manipulate them is essential for accuracy.
- Finance and Budgeting: Understanding fractions is vital for managing finances and budgets effectively. Calculating percentages, comparing loan rates, and understanding proportions all involve working with fractions.
- Data Analysis: Many data analysis tasks involve working with fractions and proportions. Being able to accurately compare fractions is crucial for making informed decisions based on the data.
Conclusion: Mastering Fraction Comparison
The seemingly simple question of whether 1/2 or 2/3 is greater provides a springboard for a deeper exploration of fractional arithmetic. Mastering the methods of comparing fractions – finding a common denominator, visual representation, decimal conversion, and cross-multiplication – is essential for various mathematical and real-world applications. By understanding these methods, individuals can confidently tackle more complex fraction comparisons and enhance their overall numerical reasoning skills. The ability to compare fractions accurately is a fundamental building block for success in higher-level mathematics and countless practical situations. Continuous practice and application are key to solidifying this important skill.
Latest Posts
Latest Posts
-
The Product Of 6 And A Number
Aug 22, 2025
-
What Does Brian Robeson Look Like In Hatchet
Aug 22, 2025
-
Is Flip Wilson Son David Still Alive
Aug 22, 2025
-
If Born In 1974 How Old Are You
Aug 22, 2025
-
What Is The Gcf Of 18 30
Aug 22, 2025
Related Post
Thank you for visiting our website which covers about What Is Greater 1 2 Or 2 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.