What Is Half Of 1 1 2
Kalali
Jul 03, 2025 · 5 min read
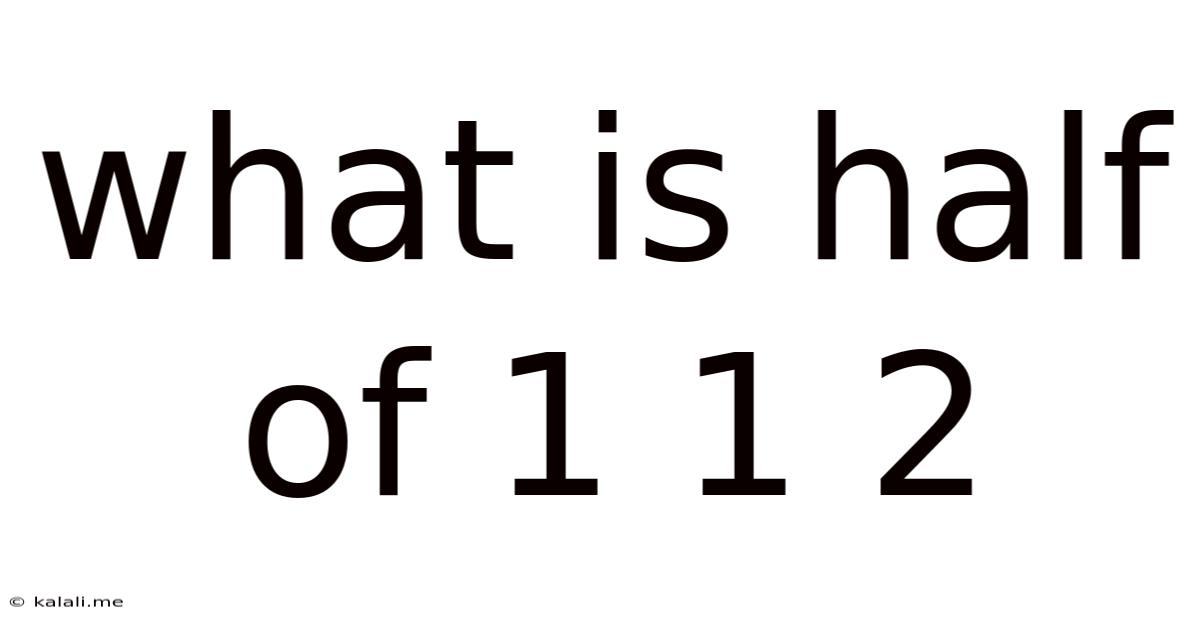
Table of Contents
What is Half of 1 1 2? Unpacking the Ambiguity and Exploring Mathematical Concepts
This seemingly simple question, "What is half of 1 1 2?", hides a fascinating ambiguity that allows us to explore several key mathematical concepts. The answer isn't immediately obvious because the notation "1 1 2" isn't standard mathematical notation. It lacks explicit operators, leaving room for interpretation. This ambiguity, however, offers a rich opportunity to delve into different approaches and highlight the importance of clear communication in mathematics. This article will explore multiple interpretations and the mathematical principles behind each.
Understanding the Ambiguity: Interpreting "1 1 2"
The core issue lies in the lack of operators between the digits. Do the numbers represent a single concatenated number, separate numbers to be added, or something else entirely? Let's examine the possibilities:
Interpretation 1: Concatenated Number
One way to interpret "1 1 2" is as the single number one hundred and twelve (112). In this case, the question becomes: "What is half of 112?"
This is a straightforward calculation: 112 / 2 = 56. Therefore, under this interpretation, half of 1 1 2 is 56.
This interpretation relies on the common practice of concatenating digits to form larger numbers. We frequently use this in everyday life, for example, when writing phone numbers or addresses.
Interpretation 2: Summation of Separate Numbers
Another plausible interpretation is that "1 1 2" represents the sum of the individual digits: 1 + 1 + 2 = 4. The question then transforms into: "What is half of 4?"
This is equally straightforward: 4 / 2 = 2. Under this interpretation, half of 1 1 2 is 2.
This interpretation highlights the importance of explicitly defining operators in mathematical expressions to avoid ambiguity. The absence of '+' signs between the digits could lead to this interpretation, particularly if the reader is used to seeing digit sums in puzzles or games.
Interpretation 3: Base Systems and Number Representation
We can extend our exploration by considering different number bases. While our standard number system is base-10 (decimal), other bases exist. This interpretation requires a deeper understanding of number systems.
For example, if "1 1 2" were a representation in a base-3 system, it would represent:
(1 * 3²) + (1 * 3¹) + (2 * 3⁰) = 9 + 3 + 2 = 14 (in base-10).
Half of 14 is 7. Therefore, under this base-3 interpretation, half of 1 1 2 is 7.
Exploring different bases demonstrates the contextual nature of mathematical notation. The same sequence of digits can represent different numerical values depending on the chosen base. This highlights the importance of clearly stating the base when working with non-decimal numbers.
Expanding the Mathematical Context: Exploring Related Concepts
The ambiguity in the original question allows us to branch out into related mathematical topics, solidifying our understanding of fundamental principles.
A. Order of Operations (PEMDAS/BODMAS)
While not directly applicable to interpretations 1 and 2, the ambiguity highlights the significance of order of operations (PEMDAS/BODMAS). If additional operators were introduced, the order in which operations are performed would become crucial. For example, if the expression were "1 + 1 x 2," the order of operations dictates that multiplication is performed before addition, resulting in 3, not 4. Understanding PEMDAS/BODMAS is crucial for solving complex mathematical problems.
B. Number Theory
Exploring different interpretations touches upon basic number theory concepts such as factorization, divisibility, and even and odd numbers. Analyzing whether the different results (56, 2, 7) are even or odd, or their prime factorization, can be a further area of investigation. For example, 56 (2 x 2 x 2 x 7) is an even number, whereas 2 is a prime number, and 7 is also a prime number.
C. Abstract Algebra
At a more advanced level, we can think of "1 1 2" as a sequence within a larger algebraic structure. In abstract algebra, sequences of numbers can be manipulated and operated on according to defined rules. This highlights how the very structure of mathematics can influence how we interpret ambiguous notation.
D. The Importance of Clear Communication in Mathematics
The exercise underscores the paramount importance of clear and unambiguous notation in mathematics. The absence of operators in "1 1 2" creates multiple valid interpretations, leading to different answers. This stresses the need for precise language and notation when formulating mathematical problems to avoid confusion and ensure accurate results. In fields like programming, scientific research, or engineering, clarity is paramount to prevent costly errors.
Conclusion: The Value of Ambiguity in Learning
While the ambiguity of "What is half of 1 1 2?" might seem like a trivial problem, it serves as a powerful pedagogical tool. It highlights the importance of precise mathematical notation, exposes different interpretations based on assumed context, and provides a springboard for exploring several fundamental mathematical concepts. It encourages critical thinking and problem-solving skills, pushing beyond rote memorization and towards a deeper understanding of the underlying principles. The multiple answers – 56, 2, and 7 – aren't wrong; they are simply different answers resulting from different interpretations. The real lesson is understanding the importance of clarity and precision to avoid such ambiguity. By exploring these different interpretations, we've not only solved a simple problem but also gained a valuable understanding of mathematical rigor and the significance of communication in this field. The seemingly simple question has ultimately opened up a world of mathematical possibilities.
Latest Posts
Latest Posts
-
5 Letter Word With 3 Vowels And 2 Consonants
Jul 30, 2025
-
1 Lb Macaroni Is How Many Cups
Jul 30, 2025
-
How To Hand Sew Two Pieces Of Fabric Together
Jul 30, 2025
-
What Is 1 4 Cup 1 4 Cup
Jul 30, 2025
-
How Many Candy Corn In A Bag
Jul 30, 2025
Related Post
Thank you for visiting our website which covers about What Is Half Of 1 1 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.