What Is Half Of 1 And 1/3 Cups
Kalali
Jul 22, 2025 · 5 min read
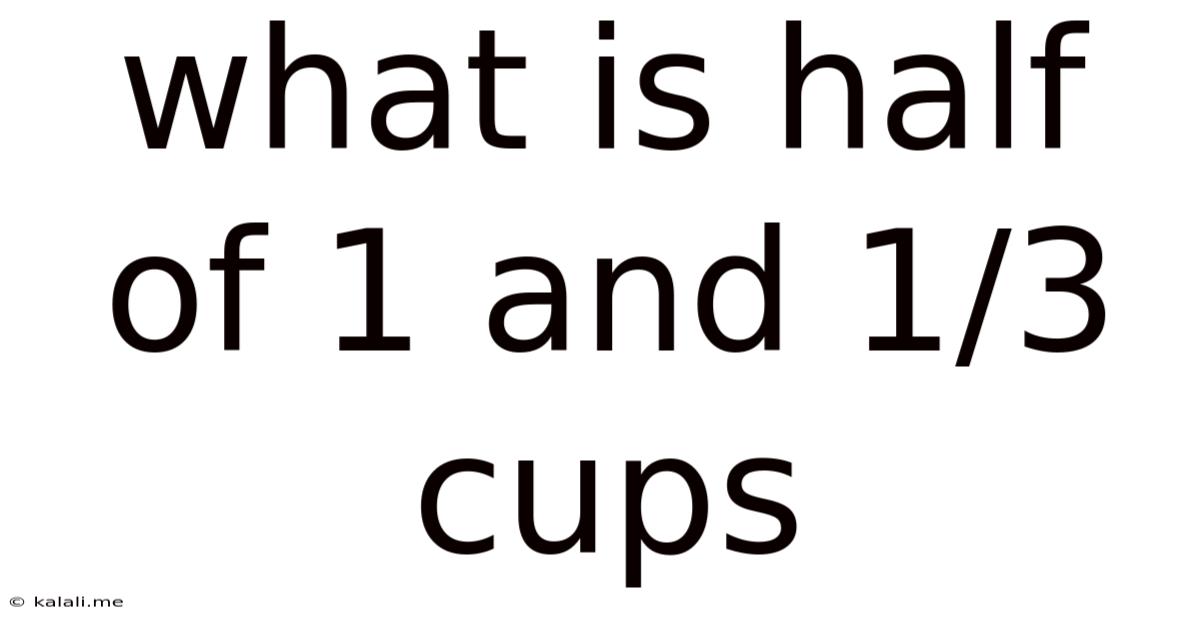
Table of Contents
What is Half of 1 and 1/3 Cups? A Comprehensive Guide to Fraction Division
This seemingly simple question – "What is half of 1 and 1/3 cups?" – actually opens a door to understanding fundamental concepts in fraction arithmetic, crucial for various applications from baking to engineering. This comprehensive guide will not only answer the question but also delve into the methodology, explore different approaches, and offer practical applications of this type of calculation. Understanding how to work with fractions is a valuable skill, and this article will equip you with the tools to confidently tackle similar problems.
Understanding the Problem: Breaking Down the Question
The core of the problem lies in understanding how to find half of a mixed number (a whole number and a fraction). "Half of" implies division by 2. Therefore, we need to divide 1 and 1/3 cups by 2. This seemingly simple task requires a solid grasp of fraction manipulation. Before we proceed, let's refresh some key concepts.
Fractions 101: A Quick Refresher
- Mixed Numbers: A mixed number combines a whole number and a fraction, like 1 and 1/3.
- Improper Fractions: An improper fraction has a numerator (top number) larger than or equal to its denominator (bottom number), such as 4/3.
- Converting Mixed Numbers to Improper Fractions: To convert a mixed number to an improper fraction, multiply the whole number by the denominator, add the numerator, and keep the same denominator. For example, 1 and 1/3 becomes (1 * 3) + 1 / 3 = 4/3.
- Dividing Fractions: To divide fractions, you multiply the first fraction by the reciprocal (inverse) of the second fraction. The reciprocal is found by flipping the numerator and denominator. For example, 1/2 divided by 2/3 is 1/2 * 3/2 = 3/4.
Method 1: Converting to an Improper Fraction and Dividing
This is the most common and generally preferred method for solving this type of problem.
-
Convert the mixed number to an improper fraction: As mentioned above, 1 and 1/3 cups is equal to 4/3 cups.
-
Rewrite the division problem: We need to find half of 4/3, which can be written as (4/3) ÷ 2.
-
Convert the whole number to a fraction: The whole number 2 can be written as 2/1.
-
Divide the fractions: To divide fractions, we multiply by the reciprocal. The reciprocal of 2/1 is 1/2. So, the calculation becomes (4/3) * (1/2).
-
Multiply the numerators and denominators: (4 * 1) / (3 * 2) = 4/6.
-
Simplify the fraction: 4/6 can be simplified by dividing both the numerator and denominator by their greatest common divisor, which is 2. This simplifies to 2/3.
Therefore, half of 1 and 1/3 cups is 2/3 cups.
Method 2: Dividing the Whole Number and Fraction Separately
This method offers a slightly different approach, useful for visualizing the problem.
-
Separate the whole number and fraction: We have 1 cup and 1/3 cup.
-
Find half of the whole number: Half of 1 cup is 1/2 cup.
-
Find half of the fraction: Half of 1/3 cup is (1/3) ÷ 2 = (1/3) * (1/2) = 1/6 cup.
-
Add the results: Combine the halves of the whole number and the fraction: 1/2 + 1/6. To add these fractions, we need a common denominator, which is 6. So, 1/2 becomes 3/6.
-
Add the fractions: 3/6 + 1/6 = 4/6.
-
Simplify the fraction: Again, we simplify 4/6 to 2/3.
Therefore, half of 1 and 1/3 cups is 2/3 cups.
Method 3: Using Decimal Conversion (Approximate Result)
While less precise for cooking and baking, converting to decimals can be useful in other contexts.
-
Convert the mixed number to a decimal: 1 and 1/3 is approximately 1.333...
-
Divide by 2: 1.333... ÷ 2 ≈ 0.666...
-
Convert back to a fraction (if needed): 0.666... is approximately 2/3.
Note: This method introduces a slight approximation due to the repeating decimal nature of 1/3. It's important to understand that this approach provides an approximate result, whereas the previous methods give the exact answer.
Practical Applications and Real-World Examples
Understanding fraction division has many practical applications:
-
Cooking and Baking: Recipes often require precise measurements. Knowing how to halve or double ingredients is essential for accurate results. If a recipe calls for 1 and 1/3 cups of flour, and you want to make half the recipe, you'll need 2/3 cups of flour.
-
Construction and Engineering: Precision is paramount in these fields. Calculations involving fractions are common when dealing with measurements and materials.
-
Sewing and Tailoring: Pattern adjustments frequently involve fractional measurements. Accurately calculating half or a quarter of a measurement is critical for proper fit and design.
-
Finance and Budgeting: Dividing budgets or calculating portions often involves fractions.
Troubleshooting Common Mistakes
- Forgetting to convert mixed numbers: Always convert mixed numbers to improper fractions before dividing.
- Incorrectly finding the reciprocal: Remember to flip the numerator and denominator when finding the reciprocal.
- Not simplifying fractions: Always simplify your final answer to its lowest terms.
- Rounding errors in decimal conversions: Be aware that decimal conversions can introduce inaccuracies, particularly with repeating decimals. Fractional methods generally provide more accurate results in these cases.
Conclusion: Mastering Fraction Division for Accurate Results
The seemingly simple task of finding half of 1 and 1/3 cups highlights the importance of understanding fraction arithmetic. This guide has explored three different methods for solving this problem, emphasizing the conversion to improper fractions as the most reliable and precise approach. Whether you're a baker needing precise ingredient measurements or an engineer working on intricate designs, mastering fraction division is an indispensable skill that will contribute to accuracy and success in various aspects of life. The ability to confidently manipulate fractions ensures accurate calculations and precise results, avoiding errors and ensuring successful outcomes in a wide array of applications. Remember to practice regularly to reinforce your understanding and build confidence in tackling similar problems.
Latest Posts
Latest Posts
-
Oil Filter Cross Reference Napa To Fram
Jul 24, 2025
-
How Many Tablespoons In A Hidden Valley Ranch Packet
Jul 24, 2025
Related Post
Thank you for visiting our website which covers about What Is Half Of 1 And 1/3 Cups . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.