What Is Half Of 3 1 2
Kalali
Jul 04, 2025 · 5 min read
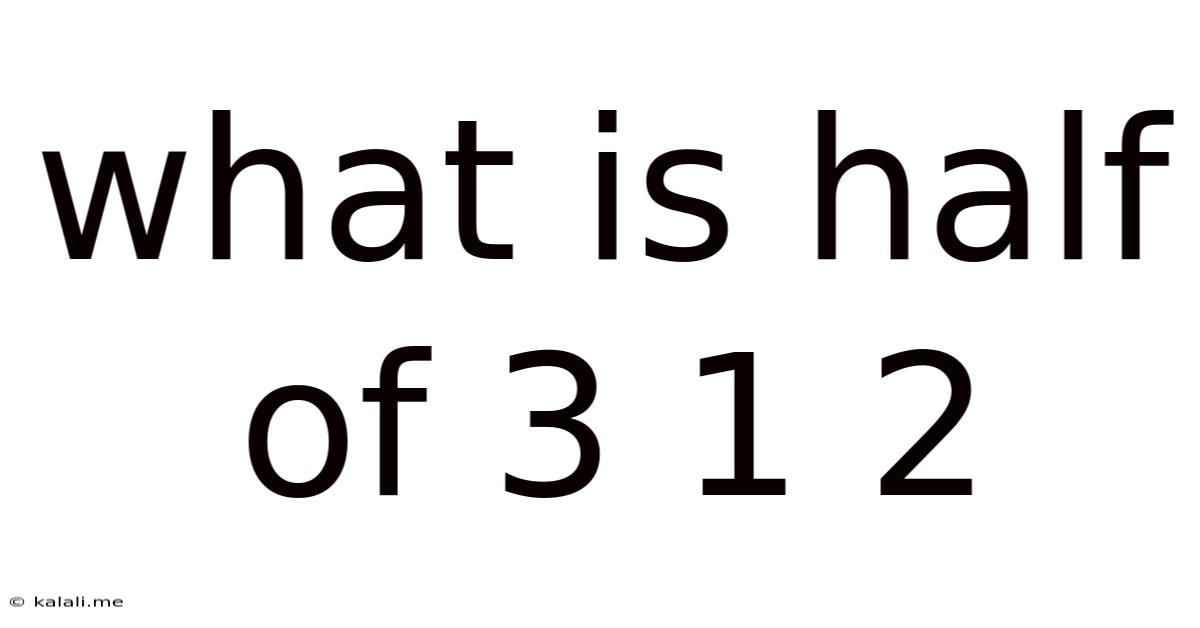
Table of Contents
What is Half of 3 1/2? A Deep Dive into Fractions and Their Applications
This seemingly simple question, "What is half of 3 1/2?", opens the door to a fascinating exploration of fractions, their manipulation, and their surprisingly broad applications in everyday life. While the answer might seem immediately obvious to some, understanding the underlying mathematical principles allows for a much deeper comprehension and empowers us to tackle more complex fractional problems with ease. This article will not only provide the answer but also delve into the various methods for solving this problem, exploring the concepts behind them and showcasing their relevance in real-world scenarios.
Understanding the Problem: Breaking Down "Half of 3 1/2"
The question asks us to find one-half (1/2) of three and one-half (3 1/2). This involves understanding how to multiply fractions and mixed numbers. Mixed numbers, like 3 1/2, combine whole numbers and fractions. Before we begin calculating, let's clarify the core concepts.
-
Fractions: Fractions represent parts of a whole. They consist of a numerator (the top number) and a denominator (the bottom number). The numerator indicates how many parts we have, while the denominator shows how many equal parts the whole is divided into.
-
Mixed Numbers: Mixed numbers, as mentioned, combine a whole number and a fraction. For example, 3 1/2 represents three whole units and one-half of another unit.
-
Multiplication of Fractions: To multiply fractions, we simply multiply the numerators together and the denominators together. For instance, (1/2) * (1/4) = 1/8.
Method 1: Converting to an Improper Fraction
This is arguably the most straightforward method. It involves converting the mixed number (3 1/2) into an improper fraction before performing the multiplication.
-
Convert 3 1/2 to an improper fraction: To do this, we multiply the whole number (3) by the denominator (2) and add the numerator (1). This result becomes the new numerator, while the denominator remains the same. Therefore, 3 1/2 becomes (3*2 + 1)/2 = 7/2.
-
Multiply the fractions: Now we multiply 1/2 by 7/2: (1/2) * (7/2) = 7/4.
-
Simplify (if necessary): The fraction 7/4 is an improper fraction (the numerator is larger than the denominator). We can convert it back to a mixed number by dividing the numerator (7) by the denominator (4): 7 ÷ 4 = 1 with a remainder of 3. Thus, 7/4 is equivalent to 1 3/4.
Method 2: Distributive Property
The distributive property of multiplication allows us to break down the problem into smaller, more manageable parts. We can multiply one-half by the whole number part and the fractional part separately, then add the results.
-
Multiply 1/2 by 3: (1/2) * 3 = 3/2 = 1 1/2
-
Multiply 1/2 by 1/2: (1/2) * (1/2) = 1/4
-
Add the results: 1 1/2 + 1/4 = 1 2/4 + 1/4 = 1 3/4
Method 3: Visual Representation
Visualizing the problem can be helpful, especially for those who prefer a more intuitive approach. Imagine a rectangular shape representing 3 1/2 units. Dividing this shape in half will give you a clear visual representation of the answer: 1 3/4. This method is particularly useful for beginners grasping the concept of fractions.
Real-World Applications of Fractions and Mixed Numbers
The seemingly simple task of finding half of 3 1/2 has far-reaching implications in various fields. Here are some examples:
-
Cooking and Baking: Recipes often require fractional measurements of ingredients. Understanding fractions is crucial for accurate measurements and successful cooking. Scaling recipes up or down requires manipulating fractions and mixed numbers.
-
Construction and Engineering: Precision is paramount in construction and engineering. Accurate measurements involving fractions and decimals are essential for building structures that are both safe and functional. Calculations involving dimensions, materials, and angles often rely heavily on fractional arithmetic.
-
Finance: Calculating interest rates, discounts, and shares often involves fractions and percentages (which are essentially fractions expressed as a hundredth). Understanding these calculations is crucial for managing personal finances and making informed investment decisions.
-
Data Analysis: In statistics and data analysis, fractions and proportions are used extensively to represent data and draw meaningful conclusions. Interpreting data visualizations often requires an understanding of fractions and ratios.
-
Sewing and Tailoring: In the world of sewing and tailoring, precise measurements are key. Working with patterns and altering clothing often involves fractions of inches or centimeters, demanding proficiency in fractional arithmetic.
-
Time Management: Dividing tasks and managing time effectively frequently involves fractional concepts. For instance, allotting 1/3 of your workday to a specific project or calculating the time remaining for a task relies on understanding fractional representation of time.
Beyond the Basics: Extending Your Understanding
The problem of finding half of 3 1/2 is a springboard to more advanced mathematical concepts. Understanding fractions thoroughly allows you to progress to more complex operations involving:
-
Adding and Subtracting Fractions: Requires finding common denominators.
-
Dividing Fractions: Involves inverting the second fraction and multiplying.
-
Working with Decimals: Converting between fractions and decimals is a valuable skill.
-
Solving Equations with Fractions: Using algebraic techniques to solve problems containing fractions.
Conclusion:
The answer to "What is half of 3 1/2?" is 1 3/4. However, the true value lies in the journey of understanding the different methods used to arrive at this solution. By exploring the concepts of fractions, mixed numbers, and their various applications, we gain a deeper appreciation for the fundamental role of fractional arithmetic in various aspects of our lives. Mastering these concepts not only solves simple problems but also equips us to handle more complex mathematical challenges with confidence and precision. This fundamental understanding serves as a robust foundation for tackling more advanced mathematical concepts in the future.
Latest Posts
Latest Posts
-
What Does Purple Mean On A Mood Necklace
Jul 04, 2025
-
How Much Is A Half A Billion Dollars
Jul 04, 2025
-
How Many Ears In A Bushel Of Corn
Jul 04, 2025
-
How Many Sheets Of Osb In A Bundle
Jul 04, 2025
-
Which Shakespeare Clown Is The Most Musical
Jul 04, 2025
Related Post
Thank you for visiting our website which covers about What Is Half Of 3 1 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.