What Is Half Of 5 1 2
Kalali
Jul 20, 2025 · 5 min read
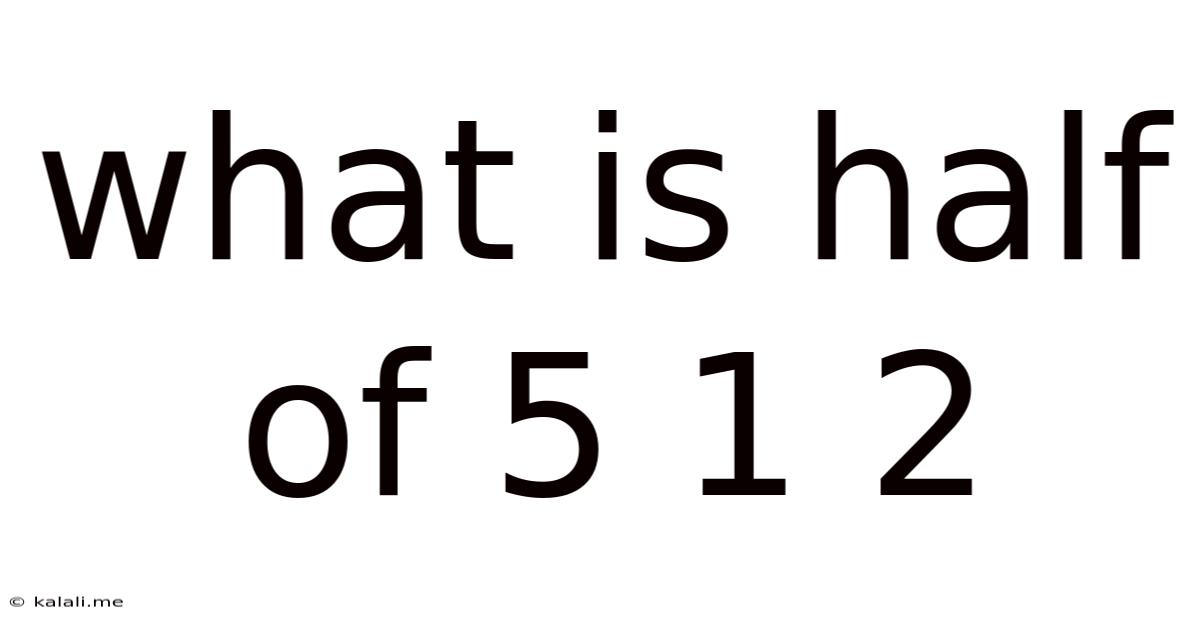
Table of Contents
What is Half of 5 1/2? A Deep Dive into Fractions and Their Applications
This seemingly simple question, "What is half of 5 1/2?", opens the door to a broader understanding of fractions, their manipulation, and their surprising relevance in everyday life. While the answer itself is straightforward, exploring the different methods to arrive at the solution reveals fundamental mathematical principles applicable far beyond this single calculation. This article will delve into various approaches to solving this problem, demonstrating different techniques and highlighting the importance of fractional arithmetic in numerous contexts.
Meta Description: Discover multiple ways to calculate half of 5 1/2, exploring the fundamentals of fraction manipulation and highlighting its real-world applications. Learn about converting mixed numbers, decimal equivalents, and the practical uses of fractional arithmetic.
Understanding the Problem: Breaking Down 5 1/2
Before we jump into the solutions, let's solidify our understanding of the question. We're asked to find half of 5 1/2. This means we need to divide 5 1/2 by 2, or find a value that, when doubled, equals 5 1/2. This involves working with a mixed number – a whole number (5) and a fraction (1/2) combined. Understanding how to handle mixed numbers is crucial for solving this and similar problems.
Method 1: Converting to an Improper Fraction
This method is a standard approach for solving fraction problems involving mixed numbers. We first convert the mixed number 5 1/2 into an improper fraction. An improper fraction has a numerator larger than or equal to its denominator.
-
Step 1: Convert to an improper fraction: To do this, multiply the whole number (5) by the denominator (2), then add the numerator (1). This gives us 11. The denominator remains the same (2). Therefore, 5 1/2 becomes 11/2.
-
Step 2: Divide by 2: Now we divide the improper fraction by 2. Dividing fractions involves multiplying by the reciprocal. The reciprocal of 2 is 1/2. So, we have (11/2) * (1/2) = 11/4.
-
Step 3: Simplify (optional): The fraction 11/4 is an improper fraction. We can convert it back to a mixed number by dividing the numerator (11) by the denominator (4). This gives us 2 with a remainder of 3. Therefore, 11/4 is equal to 2 3/4.
Method 2: Dividing the Whole Number and Fraction Separately
This method offers a more intuitive approach for some. We divide the whole number and the fractional part separately and then combine the results.
-
Step 1: Halve the whole number: Half of 5 is 5/2 = 2.5 or 2 1/2.
-
Step 2: Halve the fraction: Half of 1/2 is (1/2) * (1/2) = 1/4.
-
Step 3: Combine the results: Adding the results from steps 1 and 2, we get 2 1/2 + 1/4. To add these, we need a common denominator, which is 4. So, 2 1/2 becomes 2 2/4. Adding 2 2/4 and 1/4 gives us 2 3/4.
Method 3: Using Decimal Equivalents
This method involves converting the mixed number into a decimal and then performing the division.
-
Step 1: Convert to a decimal: 5 1/2 is equal to 5.5.
-
Step 2: Divide by 2: 5.5 / 2 = 2.75.
-
Step 3: Convert back to a fraction (optional): 2.75 can be written as 2 and 75/100. Simplifying this fraction by dividing both numerator and denominator by 25 gives us 2 and 3/4.
Real-World Applications of Fractional Arithmetic
The seemingly simple problem of finding half of 5 1/2 has far-reaching applications in various real-world scenarios. Understanding fractions and their manipulation is vital in many fields:
-
Cooking and Baking: Recipes often require precise measurements, frequently using fractions like 1/2, 1/4, and 1/3 cups or tablespoons. Scaling a recipe up or down necessitates a firm grasp of fractional arithmetic. For example, if a recipe calls for 5 1/2 cups of flour and you want to halve the recipe, you'll need to calculate half of 5 1/2 cups.
-
Construction and Engineering: Precise measurements are crucial in construction and engineering. Calculations involving fractions are common when dealing with dimensions, materials, and angles.
-
Finance: Calculating interest, discounts, and proportions often involves working with fractions and percentages, which are essentially fractions expressed as parts of 100.
-
Data Analysis: Understanding and interpreting data often involves calculating proportions and percentages, which are directly related to fractional arithmetic. Data scientists frequently use fractions to represent probabilities and proportions within datasets.
-
Sewing and Tailoring: Patterns and measurements in sewing and tailoring rely heavily on fractional precision. Adjusting patterns or calculating fabric needs often necessitates fractional calculations.
Beyond the Basics: Advanced Fraction Concepts
While this article focused on a relatively simple fractional calculation, mastering fractions opens the door to more advanced mathematical concepts:
-
Algebra: Fractions are fundamental to algebraic equations and manipulations. Solving for unknown variables often involves working with fractions.
-
Calculus: Differential and integral calculus, which are cornerstones of higher-level mathematics and physics, rely heavily on a deep understanding of fractional and rational functions.
-
Probability and Statistics: Fractions are ubiquitous in probability and statistics, representing the likelihood of events or proportions within a population.
Conclusion: The Importance of Mastering Fractions
The question "What is half of 5 1/2?" might seem trivial at first glance. However, exploring its solution reveals the fundamental importance of understanding and mastering fractional arithmetic. The ability to confidently manipulate fractions is a crucial skill, not only for academic success but also for navigating numerous aspects of everyday life and professional endeavors. This article provided three different approaches to solving this problem, demonstrating the flexibility and versatility of working with fractions, and highlighted their relevance across a wide range of disciplines. Mastering fractions equips individuals with a valuable tool for problem-solving in diverse contexts, underscoring their enduring importance in mathematics and beyond. The answer, 2 3/4, is just the beginning of a much larger and fascinating mathematical journey.
Latest Posts
Latest Posts
-
Where To Find Poppy Seeds In Grocery Store
Jul 20, 2025
-
How Many Miles Are In 32 Km
Jul 20, 2025
-
Do Directors Make More Money Than Actors
Jul 20, 2025
-
4 Oz Of Chocolate Chips In Cups
Jul 20, 2025
-
How Much Is A Half A Liter Of Water
Jul 20, 2025
Related Post
Thank you for visiting our website which covers about What Is Half Of 5 1 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.