What Is Half Of 5 3 8
Kalali
Jun 29, 2025 · 6 min read
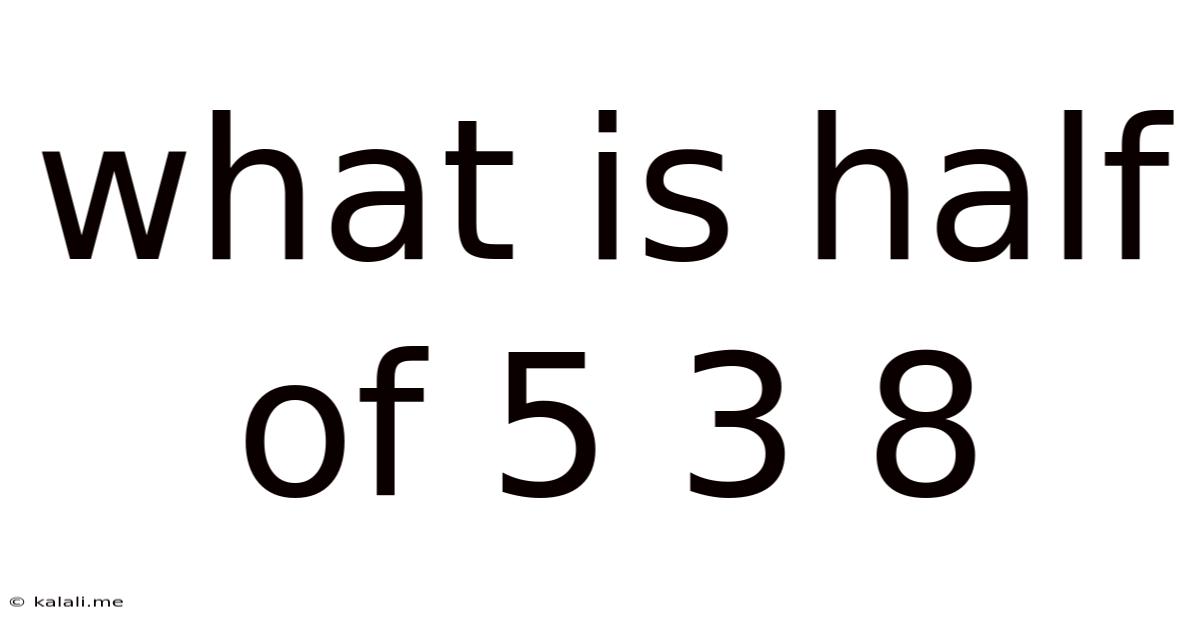
Table of Contents
Decoding "Half of 5 3 8": A Deep Dive into Number Systems and Fractional Representation
What is half of 5 3 8? This seemingly simple question opens a fascinating exploration into different number systems and the nuanced ways we represent fractions. At first glance, it appears straightforward, but a closer examination reveals layers of interpretation depending on how we understand "5 3 8". Is this a single number expressed in an unusual format, a mixed number, or perhaps something else entirely? This article will delve into these possibilities, examining different mathematical approaches and clarifying the ambiguity. We'll explore the core concepts of mixed numbers, improper fractions, decimal representations, and how these relate to finding half of a given value.
Understanding the Ambiguity of "5 3 8"
The core challenge lies in deciphering the meaning behind "5 3 8". There are several interpretations:
-
Mixed Number Interpretation: The most likely interpretation is that "5 3 8" represents a mixed number, a number that combines a whole number and a fraction. In this case, it would be read as "five and three-eighths," which is mathematically written as 5 3/8.
-
Concatenated Number Interpretation: Another possibility, although less probable given typical mathematical notation, is that "5 3 8" represents a concatenated number, meaning the digits are simply placed together without implicit mathematical operations. This would result in the number 538.
-
Other Interpretations: While less likely, there could be other interpretations depending on the context in which this expression was presented. For example, it could represent coordinates, a code, or part of a larger mathematical expression.
Given the context of the question – "What is half of 5 3 8?" – the mixed number interpretation (5 3/8) is the most logical and will be the primary focus of this article.
Calculating Half of 5 3/8: A Step-by-Step Guide
To find half of 5 3/8, we must first convert the mixed number into an improper fraction. This is a fraction where the numerator (the top number) is greater than or equal to the denominator (the bottom number). This conversion is crucial for easier calculation.
1. Converting the Mixed Number to an Improper Fraction:
To convert 5 3/8 to an improper fraction, we follow these steps:
- Multiply the whole number by the denominator: 5 * 8 = 40
- Add the numerator: 40 + 3 = 43
- Keep the same denominator: 8
Therefore, 5 3/8 is equivalent to the improper fraction 43/8.
2. Finding Half of the Improper Fraction:
Now that we have the improper fraction, finding half is a simple matter of dividing by 2. We can do this by multiplying by 1/2:
(43/8) * (1/2) = 43/16
3. Converting the Improper Fraction Back to a Mixed Number (Optional):
The result, 43/16, is an improper fraction. While this is a perfectly valid answer, it's often more intuitive to express it as a mixed number. To do this:
- Divide the numerator by the denominator: 43 ÷ 16 = 2 with a remainder of 11
- The whole number part of the mixed number is the quotient: 2
- The numerator of the fractional part is the remainder: 11
- The denominator remains the same: 16
Therefore, 43/16 is equivalent to the mixed number 2 11/16.
Conclusion: Half of 5 3/8 is 43/16 or 2 11/16
Expanding on Fractional Concepts: Decimal Representation and Beyond
While the mixed number and improper fraction representations are accurate, understanding the decimal equivalent can offer further insight and clarity. Converting 43/16 to a decimal involves simple division:
43 ÷ 16 ≈ 2.6875
This decimal representation provides a different perspective on the value, allowing for easier comparison and use in various applications. The decimal representation is particularly useful when dealing with calculations involving other decimal numbers.
Exploring Alternative Interpretations: The Case of Concatenated Numbers
As previously mentioned, another, albeit less likely, interpretation of "5 3 8" is as a concatenated number – 538. In this case, calculating half is straightforward:
538 ÷ 2 = 269
This demonstrates the importance of clarifying the representation of numbers to avoid ambiguity and ensure accurate calculations. The context is crucial in determining the correct interpretation.
Real-World Applications: Where Fractions and Mixed Numbers Matter
Understanding how to work with mixed numbers and fractions isn't just an academic exercise. These concepts are fundamental in numerous real-world applications, including:
- Cooking and Baking: Recipes often involve fractional measurements of ingredients. Knowing how to halve or double recipes requires a solid understanding of fraction manipulation.
- Construction and Engineering: Precise measurements are paramount in these fields, and fractions and decimals are essential tools for accuracy.
- Finance and Budgeting: Calculating percentages, interest rates, and proportions frequently involves working with fractions and decimals.
- Data Analysis and Statistics: Understanding fractions and their decimal equivalents is crucial for interpreting data and presenting findings effectively.
Beyond the Basics: Advanced Fraction Operations
While this article focused on finding half of a mixed number, working with fractions extends far beyond this. Other important operations include:
- Addition and Subtraction of Fractions: Requires finding a common denominator.
- Multiplication of Fractions: Involves multiplying numerators and denominators separately.
- Division of Fractions: Involves inverting the second fraction and multiplying.
Mastering these operations is crucial for anyone who needs to regularly work with fractions in their daily life or professional endeavors.
Troubleshooting Common Mistakes in Fraction Calculations
Many errors arise from misunderstanding the fundamental rules of fraction manipulation. Here are some common mistakes to avoid:
- Incorrect Conversion of Mixed Numbers: Ensure you correctly multiply the whole number by the denominator before adding the numerator when converting to an improper fraction.
- Forgetting Common Denominators: When adding or subtracting fractions, remember to find a common denominator before combining the numerators.
- Incorrectly Inverting Fractions: When dividing fractions, make sure you invert the second fraction (reciprocal) before multiplying.
By carefully reviewing these steps and understanding the underlying principles, you can significantly reduce the chances of making errors in your calculations.
Conclusion: The Power of Precision in Mathematical Representation
The seemingly simple question, "What is half of 5 3 8?" highlights the importance of precise mathematical notation and understanding different number systems. We've explored the various interpretations of "5 3 8," calculated half using different approaches, and highlighted the practical applications of these concepts. Understanding fractions, mixed numbers, and their decimal equivalents is a fundamental skill with broad applications across numerous fields. By mastering these concepts, one gains a powerful tool for problem-solving and precise calculation in various aspects of life. Remember to always consider the context and choose the most appropriate representation to ensure accurate and reliable results.
Latest Posts
Latest Posts
-
Is Wiz Khalifa Related To Snoop Dogg
Jun 29, 2025
-
How Many Cups Are In A Fifth
Jun 29, 2025
-
Are Scott Hanson And Chris Hanson Related
Jun 29, 2025
-
How Many Cups Is A Fifth Of Vodka
Jun 29, 2025
-
What Is Big Gray And Lives In California
Jun 29, 2025
Related Post
Thank you for visiting our website which covers about What Is Half Of 5 3 8 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.