What Is Half Of One And A Half
Kalali
Jul 14, 2025 · 5 min read
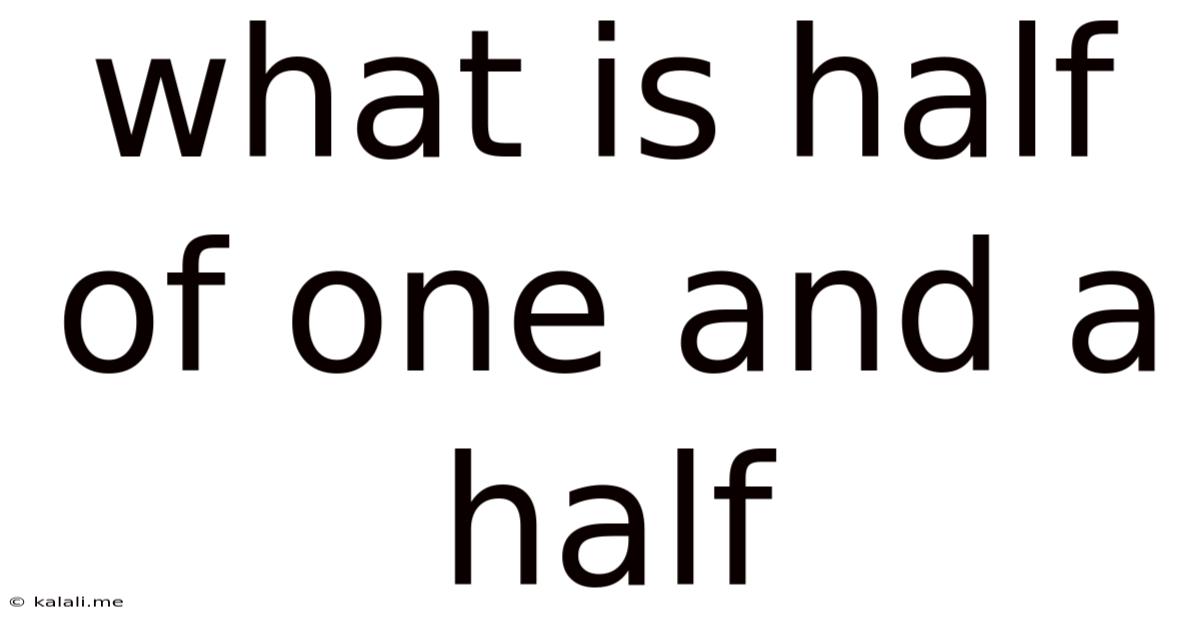
Table of Contents
What is Half of One and a Half? A Deep Dive into Fractions and Decimal Conversions
What is half of one and a half? This seemingly simple question can open the door to a deeper understanding of fractions, decimals, and mathematical operations. While the answer itself is straightforward, exploring the different methods of solving it reveals valuable insights into mathematical principles and reinforces fundamental skills. This article will delve into various approaches to solving this problem, explaining the concepts involved and providing practical examples to solidify your understanding. We'll also explore related concepts that build upon this foundation. This comprehensive guide aims to not only answer the question but also enhance your mathematical literacy.
Understanding the Problem: Deconstructing "One and a Half"
Before tackling the calculation, let's break down the core component: "one and a half." This phrase represents a mixed number – a combination of a whole number (1) and a fraction (1/2). Understanding mixed numbers is crucial for working with fractions effectively.
We can represent "one and a half" in several ways:
- Mixed Number: 1 ½
- Improper Fraction: 3/2 (This is achieved by multiplying the whole number by the denominator and adding the numerator, then placing the result over the original denominator: (1 x 2) + 1 = 3/2)
- Decimal: 1.5 (This is found by dividing the numerator of the improper fraction by the denominator: 3 ÷ 2 = 1.5)
Method 1: Working with Fractions
The most direct approach to finding half of one and a half is to work directly with the improper fraction representation.
-
Represent "one and a half" as an improper fraction: As shown above, one and a half is equal to 3/2.
-
Find half: To find half of a number, we divide it by 2, or equivalently, multiply it by 1/2. Therefore, we perform the calculation: (3/2) x (1/2).
-
Multiply the numerators and denominators: Multiply the numerators together (3 x 1 = 3) and the denominators together (2 x 2 = 4). This gives us the fraction 3/4.
Therefore, half of one and a half is 3/4.
Method 2: Working with Decimals
Alternatively, we can solve this problem using decimal representation.
-
Represent "one and a half" as a decimal: One and a half is equal to 1.5.
-
Find half: To find half, we divide by 2: 1.5 ÷ 2 = 0.75
Therefore, half of one and a half is 0.75.
Method 3: Visual Representation
A visual approach can further solidify the understanding. Imagine a circle divided into two halves. "One and a half" represents one whole circle and another half circle. To find half of this, we divide the two and a half circles into two equal parts. This results in three quarters of a circle, visually representing 3/4.
Connecting Fractions and Decimals: A Crucial Mathematical Link
The equivalence of 3/4 and 0.75 highlights the fundamental relationship between fractions and decimals. Both represent the same quantity, but in different forms. Understanding this connection is vital for mastering mathematical operations. The ability to seamlessly convert between fractions and decimals allows for flexibility in problem-solving and simplifies calculations in various contexts. This conversion is essential for tasks ranging from simple arithmetic to advanced calculus.
Expanding the Concept: Working with Other Fractions and Mixed Numbers
The principles applied to finding half of one and a half can be extended to other fractions and mixed numbers. The key is to convert mixed numbers into improper fractions before performing any calculations. This approach ensures accuracy and consistency in your mathematical operations.
Example 1: Finding 1/3 of 2 1/2
-
Convert the mixed number to an improper fraction: 2 1/2 = (2 x 2) + 1 / 2 = 5/2
-
Multiply by the fraction: (5/2) x (1/3) = 5/6
Therefore, 1/3 of 2 1/2 is 5/6.
Example 2: Finding 2/5 of 3 1/4
-
Convert the mixed number to an improper fraction: 3 1/4 = (3 x 4) + 1 / 4 = 13/4
-
Multiply by the fraction: (13/4) x (2/5) = 26/20
-
Simplify the fraction: 26/20 simplifies to 13/10 or 1 3/10
Therefore, 2/5 of 3 1/4 is 13/10 or 1 3/10.
Practical Applications: Real-World Scenarios
Understanding fractions and their manipulation is essential in numerous real-world situations. From baking and cooking (measuring ingredients) to carpentry (measuring materials) and finance (calculating percentages and proportions), the ability to work with fractions and decimals is indispensable.
Beyond the Basics: Further Exploration of Mathematical Concepts
This seemingly simple problem opens doors to more complex mathematical concepts:
- Ratio and Proportion: The concept of "half" implies a ratio of 1:2. Understanding ratios and proportions is fundamental in various fields, including science, engineering, and finance.
- Percentage Calculations: Decimals are directly related to percentages. 0.75 is equivalent to 75%. Understanding percentage calculations is crucial for financial literacy and everyday problem-solving.
- Algebraic Expressions: This problem can be expressed algebraically, providing a foundation for more advanced mathematical concepts.
Conclusion:
The question "What is half of one and a half?" while simple on the surface, offers a rich opportunity to explore fundamental mathematical concepts. By understanding the various methods of solving this problem – using fractions, decimals, and visual representations – we strengthen our mathematical literacy and build a solid foundation for tackling more complex calculations. The ability to convert between fractions and decimals, to work with mixed numbers, and to understand the underlying principles of ratios and proportions is crucial for success in various academic and real-world situations. This exploration highlights the interconnectedness of mathematical concepts and their practical applications in our daily lives.
Latest Posts
Latest Posts
-
Can You Be A Professor With A Masters
Jul 14, 2025
-
How Many Bottles Of Water Is 1 Liter
Jul 14, 2025
-
How Many Days In A Million Minutes
Jul 14, 2025
-
How Many Days Is In 11 Weeks
Jul 14, 2025
-
How Many Grams Are In One Tola Gold
Jul 14, 2025
Related Post
Thank you for visiting our website which covers about What Is Half Of One And A Half . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.