What Is Negative 2 Minus Negative 2
Kalali
Aug 24, 2025 · 5 min read
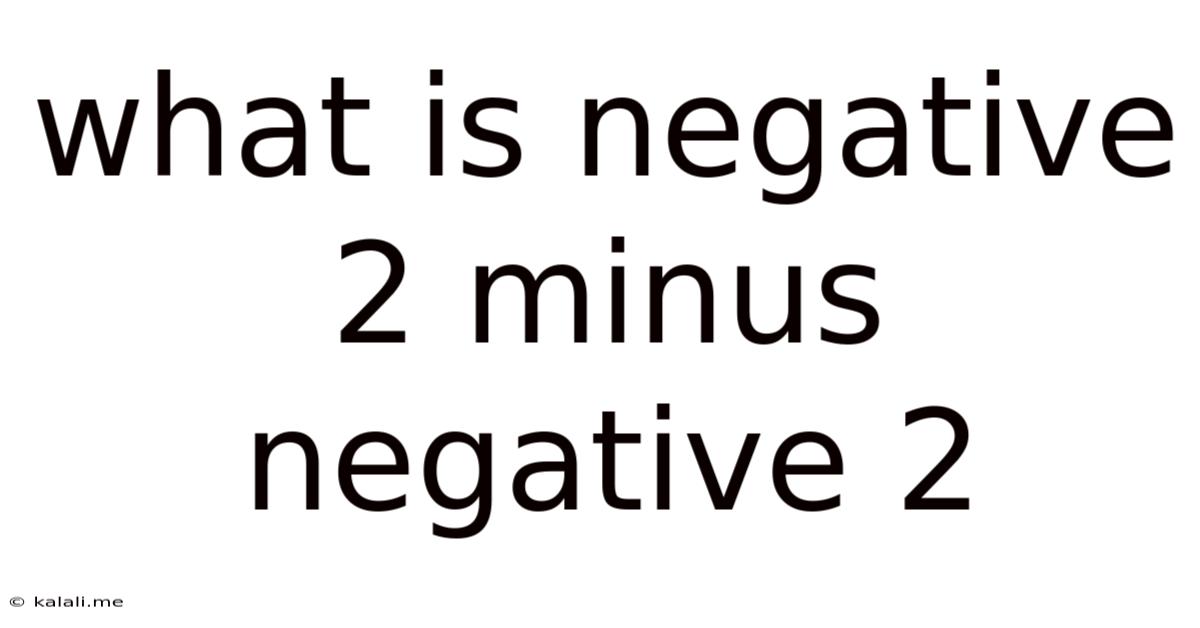
Table of Contents
What is Negative 2 Minus Negative 2? A Deep Dive into Integer Subtraction
This seemingly simple question, "What is negative 2 minus negative 2?", opens the door to a fascinating exploration of integer arithmetic, number lines, and the crucial concept of subtracting negative numbers. While the answer itself is straightforward, understanding the underlying principles solidifies a strong foundation in mathematics and enhances problem-solving skills. This article will not only answer the question but delve into the 'why' behind the solution, providing a comprehensive guide suitable for learners of all levels.
Meta Description: Learn the solution to -2 - (-2) and explore the fundamental principles of integer subtraction. This comprehensive guide explains the concept using number lines, real-world examples, and various mathematical approaches, solidifying your understanding of negative numbers.
Understanding the Basics of Integer Subtraction
Before tackling the specific problem, let's refresh our understanding of integer subtraction. Integers are whole numbers, including zero, positive numbers, and negative numbers. Subtraction, at its core, represents the process of taking away a quantity from another. When dealing with negative numbers, this process can seem counter-intuitive, but it follows consistent rules.
One helpful way to visualize subtraction is using a number line. Imagine a number line stretching from negative infinity to positive infinity. Subtracting a positive number means moving to the left on the number line, while subtracting a negative number means moving to the right. This seemingly paradoxical behavior arises from the very nature of negative numbers.
Visualizing -2 - (-2) on a Number Line
Let's use the number line to visualize the problem: -2 - (-2).
-
Start at -2: Place your finger on -2 on the number line.
-
Subtract -2: Subtracting a negative number is equivalent to adding its positive counterpart. So, subtracting -2 is the same as adding +2. Therefore, move your finger two units to the right on the number line.
-
The Result: Your finger should now be at 0. Therefore, -2 - (-2) = 0.
This visual representation clarifies the process and demonstrates the effect of subtracting a negative number. It's a crucial step in understanding the mechanics behind the operation, especially for beginners grappling with the concept of negative numbers.
The Mathematical Explanation: Double Negative Rule
The core principle at play here is the "double negative" rule, a fundamental concept in algebra. The rule states that subtracting a negative number is equivalent to adding its positive counterpart. Mathematically, this can be expressed as:
-a - (-b) = -a + b
Applying this rule to our problem:
-2 - (-2) = -2 + 2 = 0
This equation clearly shows the transformation from subtraction of a negative number to addition of a positive number. This simplification is key to solving the problem efficiently and accurately. The double negative cancels itself out, resulting in a simple addition problem.
Real-World Applications of Subtracting Negative Numbers
The concept of subtracting negative numbers might seem abstract, but it has numerous real-world applications. Consider these scenarios:
-
Temperature Changes: Imagine the temperature is -2 degrees Celsius, and it then increases by 2 degrees. This increase can be represented as -2 - (-2), resulting in a final temperature of 0 degrees Celsius. Here, subtracting the negative change (+2 degrees) reflects the temperature increase.
-
Financial Transactions: If you owe someone $2 (represented as -$2), and they forgive that debt ($2), this can be represented mathematically as -2 - (-2) = 0, signifying that your debt is now eliminated.
-
Altitude Changes: If a submarine is at a depth of -2 meters (2 meters below sea level), and it ascends by 2 meters, its new depth is 0 meters (sea level). This is another illustration of subtracting a negative value to reflect positive movement.
These examples illustrate that subtracting negative numbers is not just a mathematical abstraction but a practical tool for modeling various real-world situations involving changes and reversals. Understanding this application strengthens the practical relevance of the concept.
Different Approaches to Solving -2 - (-2)
While the number line and double negative rule provide the most intuitive methods, other mathematical approaches can also be used to arrive at the same answer:
-
Using the additive inverse: Every number has an additive inverse, a number that, when added to the original number, results in zero. The additive inverse of -2 is +2. Therefore, -2 - (-2) can be rewritten as -2 + (+2) = 0.
-
Adding zero: We can add zero to an equation without changing its value. We can rewrite -2 - (-2) as -2 + 0 - (-2). Then, we know that 0 = 2 + (-2), substituting this in gives -2 + (2 + (-2)) - (-2). This simplifies to (-2 + 2) + (-2) - (-2) = 0 + 0 = 0.
These alternative approaches demonstrate the flexibility and robustness of mathematical operations. They provide different perspectives on the same problem, leading to a deeper understanding of the underlying principles.
Expanding the Concept: More Complex Integer Subtraction
The principles discussed above can be extended to solve more complex problems involving integer subtraction. Consider the following:
-
-5 - (-3): Using the double negative rule, this becomes -5 + 3 = -2.
-
7 - (-4): This simplifies to 7 + 4 = 11.
-
-8 - (-12): This becomes -8 + 12 = 4.
By consistently applying the double negative rule and visualizing the process on a number line, even more complicated integer subtraction problems become manageable and easily solvable.
Common Mistakes to Avoid
Students often make mistakes when dealing with negative numbers. Some common errors include:
-
Ignoring the double negative: Failing to recognize that subtracting a negative is equivalent to adding a positive is a frequent source of errors.
-
Incorrect sign manipulation: Incorrectly handling the signs during the simplification process can lead to the wrong answer.
-
Misinterpreting the number line: Misunderstanding how movement on the number line corresponds to addition and subtraction can result in errors.
Conclusion: Mastering Integer Subtraction
The seemingly simple question, "What is negative 2 minus negative 2?", has led us on a journey through the fascinating world of integer arithmetic. We’ve established that the answer is 0, and we've explored this solution through various methods including the number line visualization, the double negative rule, and alternative mathematical approaches. Understanding integer subtraction is crucial for mastering more advanced mathematical concepts. By solidifying your grasp of the fundamental principles, you'll build a strong foundation for future mathematical endeavors and improve your problem-solving abilities in various contexts. Remember the double negative rule, practice using the number line, and you'll confidently navigate the world of integer subtraction.
Latest Posts
Latest Posts
-
When Organizing Your Career Portfolio You Should
Aug 25, 2025
-
Did Td Jakes Wife File For Divorce
Aug 25, 2025
-
What Is Larger 1 3 Or 1 4
Aug 25, 2025
-
Greg Read Rowleys Diary To Find Out
Aug 25, 2025
-
Pokemon Mystery Dungeon Red Rescue Team Gba Gameshark Codes
Aug 25, 2025
Related Post
Thank you for visiting our website which covers about What Is Negative 2 Minus Negative 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.