What Is Subset Of Real Numbers
Kalali
Apr 02, 2025 · 5 min read
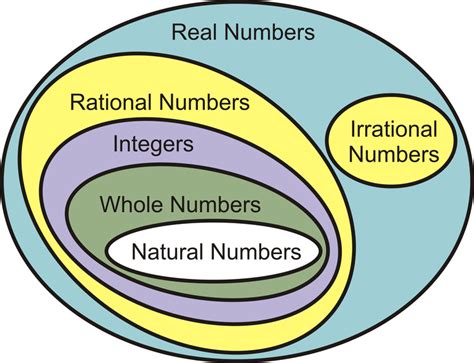
Table of Contents
What is a Subset of Real Numbers? A Comprehensive Guide
The real numbers, denoted by ℝ, form the foundation of much of mathematics and its applications. Understanding their subsets is crucial for grasping many mathematical concepts, from calculus to linear algebra and beyond. This comprehensive guide delves deep into the subsets of real numbers, exploring their definitions, properties, and significance. We'll examine key subsets with illustrative examples and explanations designed for both beginners and those seeking a deeper understanding.
The Realm of Real Numbers: A Quick Recap
Before diving into subsets, let's briefly revisit what constitutes the real numbers. The real numbers encompass all rational and irrational numbers.
-
Rational Numbers (ℚ): These numbers can be expressed as a fraction p/q, where p and q are integers, and q is not zero. Examples include 1/2, -3, 0, and 2.7 (which is 27/10). Rational numbers have either terminating or repeating decimal representations.
-
Irrational Numbers: These numbers cannot be expressed as a fraction of two integers. Their decimal representations are non-terminating and non-repeating. Famous examples include π (pi), e (Euler's number), and √2.
Key Subsets of Real Numbers
The real numbers are vast, so mathematicians categorize them into smaller, more manageable subsets based on their properties. Let's explore some of the most important ones:
1. Natural Numbers (ℕ)
Also known as counting numbers, these are the positive whole numbers: {1, 2, 3, 4, ...}. They're fundamental for counting and form the basis for many other number systems. ℕ is a subset of all other number systems discussed here.
Properties:
- Closure under addition and multiplication: Adding or multiplying two natural numbers always results in another natural number.
- Well-ordered: Every non-empty subset of natural numbers has a least element. This property is crucial in mathematical induction proofs.
2. Whole Numbers (ℤ₀ or ℕ₀)
This set extends the natural numbers by including zero: {0, 1, 2, 3, 4, ...}. The inclusion of zero is significant, particularly in algebra and various mathematical applications.
Properties:
- It inherits the closure under addition and multiplication from natural numbers.
- Zero acts as an additive identity (a + 0 = a).
3. Integers (ℤ)
Integers include all positive and negative whole numbers, along with zero: {..., -3, -2, -1, 0, 1, 2, 3, ...}. They are essential for representing quantities that can be both positive and negative, such as temperature or financial balance.
Properties:
- Closed under addition, subtraction, and multiplication.
- Every integer has an additive inverse (a + (-a) = 0).
4. Rational Numbers (ℚ) - Revisited
As mentioned earlier, rational numbers are those that can be expressed as a fraction of two integers. They form a dense subset of the real numbers, meaning between any two rational numbers, there exists another rational number.
Properties:
- Closed under addition, subtraction, multiplication, and division (excluding division by zero).
- They have either terminating or repeating decimal expansions.
5. Irrational Numbers (ℝ \ ℚ)
Irrational numbers are the real numbers that are not rational. They have non-terminating and non-repeating decimal expansions. Many important mathematical constants, like π and e, are irrational.
Properties:
- They cannot be expressed as a fraction of two integers.
- Their decimal expansions are infinite and non-repeating.
- They are also dense in the real numbers.
6. Real Numbers (ℝ) - The Big Picture
The real numbers encompass all rational and irrational numbers. They form a complete ordered field, meaning they satisfy a specific set of axioms that define their properties. The real number line is a visual representation of this set, where each point corresponds to a unique real number.
Properties:
- Completeness: Every Cauchy sequence of real numbers converges to a real number. This is a crucial property for calculus and analysis.
- Order: Real numbers can be ordered (a < b, a = b, or a > b).
- Field axioms: Real numbers satisfy the axioms of a field (addition, subtraction, multiplication, division, etc.).
7. Subsets Defined by Intervals
Real numbers can also be grouped into subsets defined by intervals on the real number line. These are defined using inequalities:
- Open Interval: (a, b) = {x ∈ ℝ | a < x < b}. The endpoints a and b are not included.
- Closed Interval: [a, b] = {x ∈ ℝ | a ≤ x ≤ b}. The endpoints a and b are included.
- Half-Open Intervals: (a, b] = {x ∈ ℝ | a < x ≤ b} and [a, b) = {x ∈ ℝ | a ≤ x < b}.
8. Other Important Subsets
Beyond the fundamental subsets, many others exist, often defined based on specific properties:
- Even Numbers: Integers divisible by 2.
- Odd Numbers: Integers not divisible by 2.
- Prime Numbers: Natural numbers greater than 1 that are only divisible by 1 and themselves.
- Composite Numbers: Natural numbers greater than 1 that are not prime.
- Algebraic Numbers: Numbers that are roots of a polynomial equation with integer coefficients.
- Transcendental Numbers: Numbers that are not algebraic (e.g., π and e).
Applications and Significance
Understanding these subsets is paramount in various mathematical fields and applications:
- Calculus: Understanding intervals is crucial for defining limits, derivatives, and integrals.
- Linear Algebra: Real numbers form the scalars in vector spaces.
- Probability and Statistics: Real numbers represent probabilities and statistical measures.
- Computer Science: Representing and manipulating real numbers in computers involves careful consideration of their subsets and limitations due to finite precision.
Conclusion
The subsets of real numbers provide a powerful framework for organizing and understanding the vast landscape of numbers. From the simplicity of natural numbers to the complexities of irrational and transcendental numbers, each subset plays a vital role in mathematics and its numerous applications. A firm grasp of these subsets is essential for anyone pursuing further studies in mathematics or any field that relies heavily on mathematical concepts. This comprehensive overview has aimed to illuminate these subsets and their importance, fostering a deeper appreciation for the rich structure of the real number system. Further exploration into specific subsets and their unique properties will undoubtedly enrich your understanding of mathematics as a whole.
Latest Posts
Latest Posts
-
True Or False Prehistoric Humans Felt Stress
Apr 03, 2025
-
120 Out Of 150 As A Percentage
Apr 03, 2025
-
Cuanto Son 40 Onzas En Litros
Apr 03, 2025
-
What Is 19 Out Of 25
Apr 03, 2025
-
Cuantos Grados Son 64 Fahrenheit En Centigrados
Apr 03, 2025
Related Post
Thank you for visiting our website which covers about What Is Subset Of Real Numbers . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
