What Is The Fraction For 0.375
Kalali
Apr 23, 2025 · 5 min read
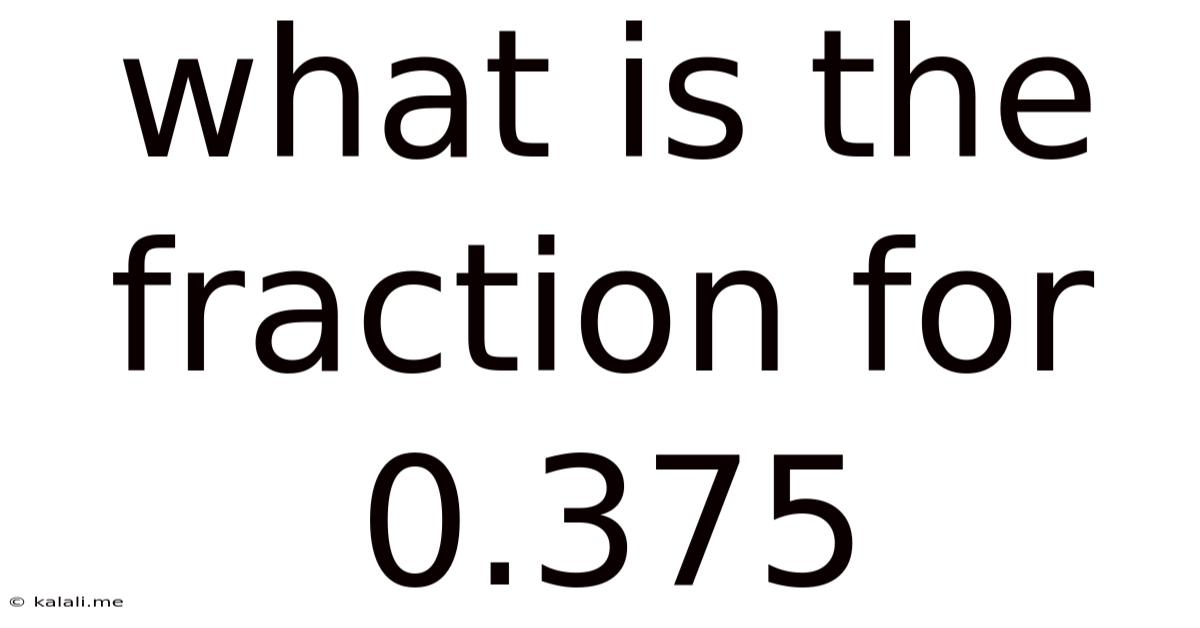
Table of Contents
What is the Fraction for 0.375? A Deep Dive into Decimal to Fraction Conversion
The seemingly simple question, "What is the fraction for 0.375?", opens a door to a fascinating world of mathematical concepts. While the answer itself is straightforward, understanding the process of converting decimals to fractions reveals fundamental principles of number systems and provides valuable skills applicable in various fields, from basic arithmetic to advanced calculus. This article will not only answer the question directly but also explore the underlying mechanics, different approaches, and practical applications of decimal-to-fraction conversions.
Meta Description: Learn how to convert decimals to fractions with a detailed explanation of the process, using 0.375 as an example. Discover different methods and practical applications of this essential mathematical skill.
The immediate answer to the question, "What is the fraction for 0.375?", is 3/8. But let's delve deeper into how we arrive at this solution and explore the broader context of decimal-fraction conversion.
Understanding Decimal and Fraction Representation
Before diving into the conversion process, it's crucial to understand the fundamental difference between decimal and fraction representations of numbers.
-
Decimals: Decimals represent numbers as a sum of powers of 10. Each digit to the right of the decimal point represents a fraction with a denominator that is a power of 10 (10, 100, 1000, and so on). For instance, 0.375 can be broken down as 3/10 + 7/100 + 5/1000.
-
Fractions: Fractions represent numbers as a ratio of two integers, a numerator (top number) and a denominator (bottom number). They represent parts of a whole. The fraction 3/8 means 3 out of 8 equal parts.
The process of converting a decimal to a fraction involves transforming the decimal representation into an equivalent ratio of two integers.
Method 1: Using the Place Value Method
This is perhaps the most intuitive method, especially for decimals with a limited number of digits after the decimal point. Let's apply this to 0.375:
-
Identify the place value of the last digit: The last digit, 5, is in the thousandths place. This means the denominator of our fraction will be 1000.
-
Write the decimal as a fraction: The decimal 0.375 can be written as the fraction 375/1000.
-
Simplify the fraction: Now, we need to simplify the fraction to its lowest terms. This involves finding the greatest common divisor (GCD) of the numerator (375) and the denominator (1000) and dividing both by it. The GCD of 375 and 1000 is 125.
-
Simplify and arrive at the final answer: Dividing both the numerator and the denominator by 125, we get: 375 ÷ 125 = 3 and 1000 ÷ 125 = 8. Therefore, the simplified fraction is 3/8.
Method 2: Using the Power of 10 Method
This method is closely related to the place value method but emphasizes the concept of powers of 10. It's particularly useful for understanding the underlying mathematical principles.
-
Express the decimal as a fraction with a power of 10 as the denominator: 0.375 can be written as 375/1000 (since 1000 = 10³).
-
Find the prime factorization of the numerator and denominator:
- 375 = 3 × 5³
- 1000 = 2³ × 5³
-
Simplify by canceling common factors: Both the numerator and the denominator share a factor of 5³. Canceling these factors, we are left with 3/2³.
-
Calculate the simplified fraction: 2³ = 8, so the simplified fraction is 3/8.
Method 3: Using Repeated Division (for recurring decimals)
While 0.375 is a terminating decimal (it ends after a finite number of digits), this method is crucial for converting recurring or repeating decimals to fractions. For example, consider 0.333... (0.3 recurring):
-
Let x equal the recurring decimal: x = 0.333...
-
Multiply x by a power of 10 to shift the decimal point: 10x = 3.333...
-
Subtract the original equation from the new equation: 10x - x = 3.333... - 0.333... This simplifies to 9x = 3.
-
Solve for x: x = 3/9 = 1/3.
This method demonstrates a powerful technique for handling repeating decimals, which cannot be directly converted using the place value method.
Practical Applications of Decimal to Fraction Conversions
The ability to convert decimals to fractions is not just an academic exercise; it's a valuable skill with diverse applications:
-
Baking and Cooking: Recipes often use fractions for ingredient measurements. Converting decimal measurements from a digital scale to fractions for easier understanding and consistency is essential.
-
Engineering and Construction: Precise measurements are paramount in engineering and construction. Converting decimal measurements to fractions ensures accuracy and compatibility with standard measurement systems.
-
Finance and Accounting: Understanding fractions is crucial for handling percentages, interest rates, and financial ratios accurately.
-
Science and Data Analysis: Scientific measurements and data analysis often involve working with fractions and decimals interchangeably.
-
Software Development: Programming often requires converting between different number representations for accurate calculations and data manipulation.
Beyond 0.375: Tackling More Complex Decimals
The methods described above can be applied to convert any decimal, whether terminating or recurring, into its fractional equivalent. For more complex decimals, employing the power of 10 method and simplifying using prime factorization often leads to the most efficient solution. Remember, the key is to find the greatest common divisor of the numerator and denominator to simplify the fraction to its lowest terms.
Conclusion
Converting 0.375 to a fraction, resulting in 3/8, is a straightforward process. However, understanding the underlying methods and their applications extends far beyond this single example. Mastering decimal-to-fraction conversion empowers you with a fundamental mathematical skill applicable across various disciplines and contexts. Whether you're following a recipe, working on an engineering project, or analyzing data, the ability to seamlessly translate between decimal and fractional representations is invaluable. This article provided a comprehensive guide, incorporating several different approaches to help solidify your understanding of this important mathematical concept.
Latest Posts
Latest Posts
-
What Is The Importance Of Crossing Over
Apr 23, 2025
-
Which Unit Is Used To Measure Force
Apr 23, 2025
-
Cuanto Es 6 Onzas En Ml
Apr 23, 2025
-
How To Identify A Redox Reaction
Apr 23, 2025
-
How Many Oz In 75 Ml
Apr 23, 2025
Related Post
Thank you for visiting our website which covers about What Is The Fraction For 0.375 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.