What Is The Gcf Of 10 And 25
Kalali
Jul 20, 2025 · 5 min read
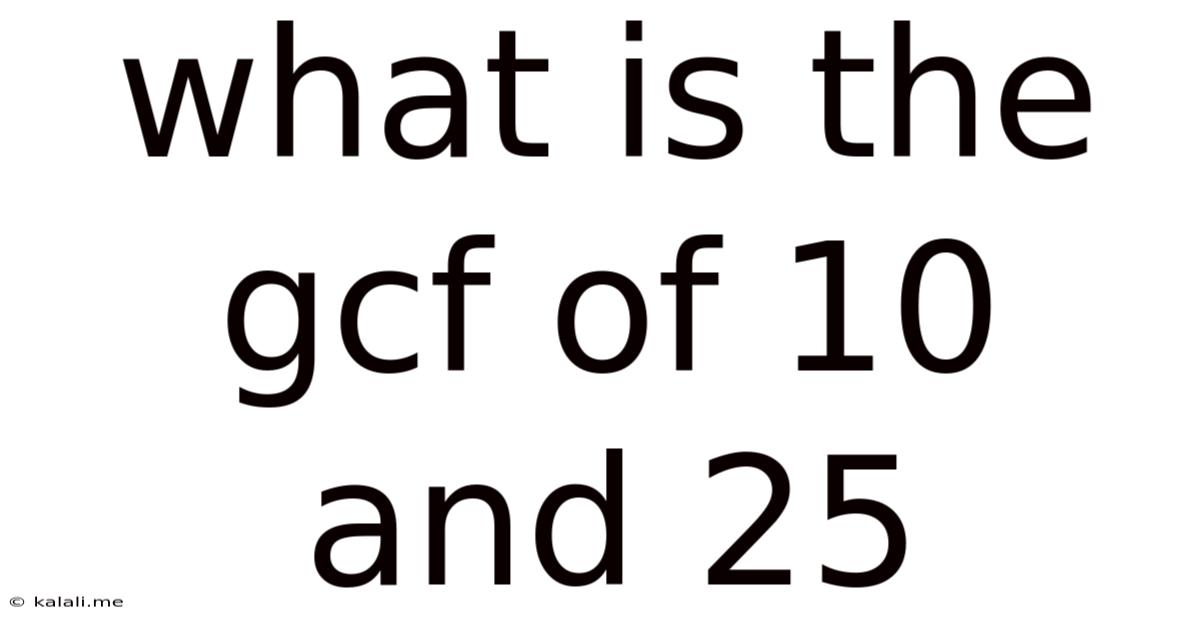
Table of Contents
Unveiling the GCF: A Deep Dive into the Greatest Common Factor of 10 and 25
Finding the greatest common factor (GCF) of two numbers might seem like a simple arithmetic task, but understanding the underlying concepts and exploring different methods can unlock a deeper appreciation of number theory and its applications. This article will delve into the GCF of 10 and 25, demonstrating various techniques to calculate it and exploring the broader implications of GCF in mathematics and beyond. We'll go beyond a simple answer and examine the process, offering a comprehensive guide suitable for students and anyone curious about the intricacies of number theory.
Meta Description: Discover the greatest common factor (GCF) of 10 and 25 through various methods, exploring prime factorization, the Euclidean algorithm, and the significance of GCF in mathematics and real-world applications. This comprehensive guide simplifies a fundamental concept in number theory.
Understanding the Greatest Common Factor (GCF)
Before we tackle the specific case of 10 and 25, let's establish a clear understanding of what the GCF actually represents. The greatest common factor, also known as the greatest common divisor (GCD), is the largest positive integer that divides each of the integers without leaving a remainder. In simpler terms, it's the biggest number that goes evenly into both numbers. This concept is fundamental in various areas of mathematics, including simplifying fractions, solving equations, and understanding number relationships.
Method 1: Prime Factorization
This is perhaps the most intuitive method for finding the GCF. It involves breaking down each number into its prime factors – the smallest prime numbers that multiply together to give the original number. Let's apply this to 10 and 25:
- Prime factorization of 10: 2 x 5
- Prime factorization of 25: 5 x 5
Now, we identify the common prime factors. Both 10 and 25 share a single prime factor: 5. The GCF is the product of these common prime factors. In this case, the GCF(10, 25) = 5.
Method 2: Listing Factors
This method is particularly useful for smaller numbers. We list all the factors (numbers that divide evenly) of each number and then identify the largest factor they have in common.
- Factors of 10: 1, 2, 5, 10
- Factors of 25: 1, 5, 25
Comparing the two lists, we see that the common factors are 1 and 5. The greatest of these common factors is 5. Therefore, the GCF(10, 25) = 5. This method is straightforward but becomes less efficient as the numbers get larger.
Method 3: The Euclidean Algorithm
The Euclidean algorithm is a highly efficient method for finding the GCF of two numbers, especially when dealing with larger numbers. It's based on the principle that the GCF of two numbers does not change if the larger number is replaced by its difference with the smaller number. This process is repeated until the two numbers are equal, and that number is the GCF.
Let's apply the Euclidean algorithm to 10 and 25:
- Start with the larger number (25) and the smaller number (10).
- Subtract the smaller number from the larger number: 25 - 10 = 15. Now we have 10 and 15.
- Repeat the process: 15 - 10 = 5. Now we have 10 and 5.
- Repeat again: 10 - 5 = 5. Now we have 5 and 5.
- The numbers are equal, so the GCF is 5.
The Euclidean algorithm provides a systematic and efficient way to find the GCF, regardless of the size of the numbers. This method is particularly advantageous when working with larger numbers where prime factorization might become cumbersome.
Significance of the GCF
Understanding the GCF is more than just an academic exercise; it has practical applications across various fields:
-
Simplifying Fractions: The GCF is crucial for simplifying fractions to their lowest terms. For example, the fraction 10/25 can be simplified by dividing both the numerator and the denominator by their GCF (5), resulting in the equivalent fraction 2/5.
-
Solving Equations: The GCF plays a role in solving Diophantine equations, which involve finding integer solutions to algebraic equations.
-
Geometry: GCF is used in geometry problems involving dividing shapes into equal parts or finding the dimensions of similar figures.
-
Modular Arithmetic: The GCF is fundamental in modular arithmetic, a branch of number theory with applications in cryptography and computer science.
-
Music Theory: The GCF helps in understanding musical intervals and harmony.
Beyond the Basics: Exploring Related Concepts
Understanding the GCF opens doors to exploring more advanced concepts in number theory:
-
Least Common Multiple (LCM): The LCM is the smallest positive integer that is a multiple of both numbers. The relationship between GCF and LCM is given by the formula: LCM(a, b) * GCF(a, b) = a * b. For 10 and 25, the LCM is 50.
-
Coprime Numbers: Two numbers are considered coprime (or relatively prime) if their GCF is 1. For example, 15 and 28 are coprime.
-
Divisibility Rules: Understanding GCF can help in applying divisibility rules, which are shortcuts to determine if a number is divisible by another number without performing the actual division.
Conclusion: The Power of a Simple Concept
While the GCF of 10 and 25 might seem trivial at first glance, the journey of discovering it unveils a world of mathematical concepts and applications. From the simple methods of prime factorization and listing factors to the efficient Euclidean algorithm, the process itself is educational. Understanding the GCF is not merely about finding a single number; it's about grasping the fundamental principles of number theory and appreciating its importance in diverse fields. This knowledge provides a solid foundation for further exploration of mathematical concepts and their real-world implications. The seemingly simple question, "What is the GCF of 10 and 25?" opens a door to a deeper understanding of the intricate beauty of mathematics. The answer, 5, is just the beginning.
Latest Posts
Latest Posts
-
How Many Ounces In A Quarter Teaspoon
Jul 21, 2025
-
How Many Cups In 3 Lbs Of Sour Cream
Jul 21, 2025
-
How Many Grams In 1 Cup Of Rice
Jul 21, 2025
-
Which Pair Of Lines Demonstrates Slant Rhyme
Jul 21, 2025
-
The Triangles Shown Below Must Be Congruent
Jul 21, 2025
Related Post
Thank you for visiting our website which covers about What Is The Gcf Of 10 And 25 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.