What Is The Gcf Of 36 And 45
Kalali
Aug 23, 2025 · 6 min read
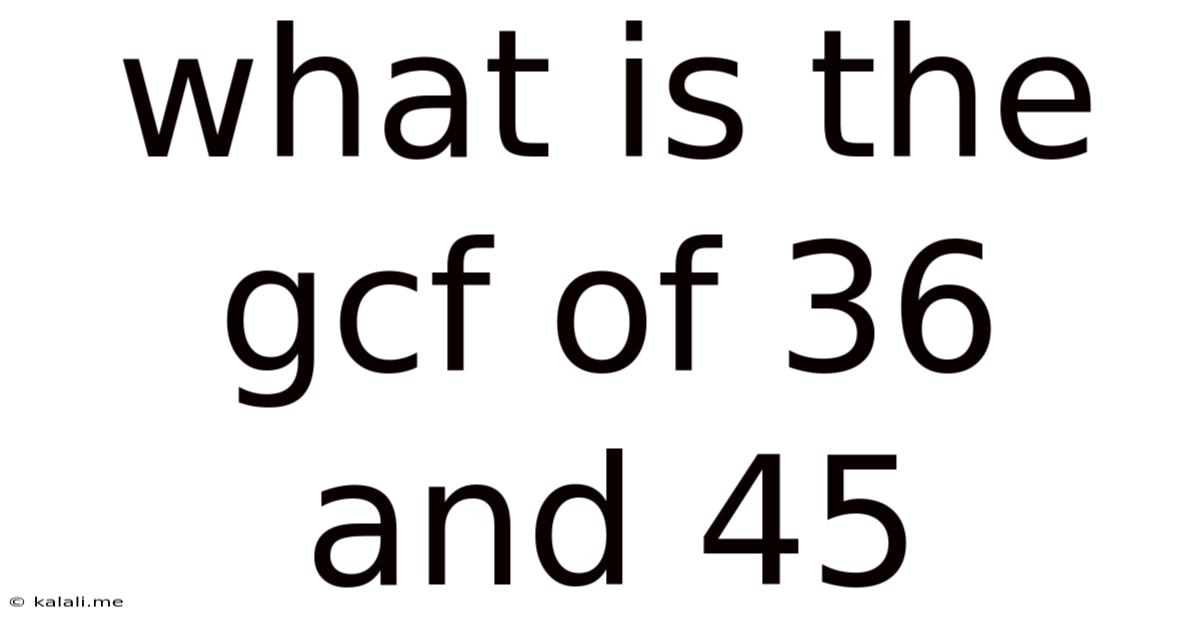
Table of Contents
Unveiling the Greatest Common Factor (GCF) of 36 and 45: A Comprehensive Guide
Finding the greatest common factor (GCF), also known as the greatest common divisor (GCD), of two numbers might seem like a simple arithmetic problem. However, understanding the underlying concepts and various methods for calculating the GCF is crucial, not just for basic math but also for more advanced applications in algebra, number theory, and even computer science. This article will delve deep into the GCF of 36 and 45, explaining various methods to find it and exploring the broader implications of this fundamental concept. We'll explore the practical uses of GCF and demonstrate how to solve similar problems.
What is the Greatest Common Factor (GCF)?
The greatest common factor (GCF) of two or more integers is the largest positive integer that divides each of the integers without leaving a remainder. In simpler terms, it's the biggest number that can perfectly divide both numbers. For example, the GCF of 12 and 18 is 6 because 6 is the largest number that divides both 12 and 18 evenly. Understanding the GCF is essential for simplifying fractions, solving algebraic equations, and various other mathematical operations.
Methods for Finding the GCF
Several methods can be used to determine the GCF of two numbers. Let's explore the most common ones, focusing on how they apply to finding the GCF of 36 and 45.
1. Listing Factors Method:
This is the most straightforward approach, especially for smaller numbers. We list all the factors of each number and then identify the largest factor common to both.
- Factors of 36: 1, 2, 3, 4, 6, 9, 12, 18, 36
- Factors of 45: 1, 3, 5, 9, 15, 45
Comparing the two lists, we see that the common factors are 1, 3, and 9. The largest of these common factors is 9. Therefore, the GCF of 36 and 45 is 9.
2. Prime Factorization Method:
This method involves expressing each number as a product of its prime factors. The GCF is then found by multiplying the common prime factors raised to their lowest powers.
- Prime factorization of 36: 2² × 3² (36 = 2 x 2 x 3 x 3)
- Prime factorization of 45: 3² × 5 (45 = 3 x 3 x 5)
The common prime factor is 3, and its lowest power is 3². Therefore, the GCF of 36 and 45 is 3² = 9.
3. Euclidean Algorithm:
The Euclidean algorithm is a highly efficient method for finding the GCF of two numbers, especially when dealing with larger numbers. It involves repeatedly applying the division algorithm until the remainder is 0. The last non-zero remainder is the GCF.
Let's apply the Euclidean algorithm to 36 and 45:
- Divide the larger number (45) by the smaller number (36): 45 ÷ 36 = 1 with a remainder of 9.
- Replace the larger number with the smaller number (36) and the smaller number with the remainder (9): 36 ÷ 9 = 4 with a remainder of 0.
Since the remainder is 0, the GCF is the last non-zero remainder, which is 9.
Understanding the Significance of the GCF
The GCF has numerous practical applications across various mathematical and real-world scenarios:
-
Simplifying Fractions: The GCF is crucial for simplifying fractions to their lowest terms. For example, the fraction 36/45 can be simplified by dividing both the numerator and denominator by their GCF (9), resulting in the simplified fraction 4/5.
-
Solving Equations: The GCF plays a vital role in solving certain types of algebraic equations, particularly those involving factoring.
-
Geometry Problems: The GCF is frequently used in geometry problems involving finding the dimensions of objects or determining the greatest possible size of square tiles that can perfectly cover a rectangular area. For instance, if you have a rectangular area of 36 inches by 45 inches, the largest square tiles you could use without cutting any would be 9 inches x 9 inches.
-
Number Theory: The GCF is a fundamental concept in number theory, used in various theorems and proofs related to prime numbers, divisibility, and modular arithmetic.
-
Computer Science: The Euclidean algorithm, a method for finding the GCF, is widely used in computer science for various cryptographic applications and other computational tasks. Its efficiency makes it a preferred choice for handling large numbers.
GCF and LCM: A Complementary Relationship
The GCF is closely related to the least common multiple (LCM). The LCM of two numbers is the smallest positive integer that is a multiple of both numbers. There's a simple relationship between the GCF and LCM of two numbers (a and b):
GCF(a, b) × LCM(a, b) = a × b
For 36 and 45:
GCF(36, 45) = 9 LCM(36, 45) = 180
9 × 180 = 1620 36 × 45 = 1620
This relationship demonstrates the interconnectedness of these two fundamental concepts in number theory.
Extending the Concept: GCF of More Than Two Numbers
The methods described above can be extended to find the GCF of more than two numbers. For the prime factorization method, you would find the prime factorization of each number and then identify the common prime factors raised to their lowest powers. For the Euclidean algorithm, you would repeatedly apply the algorithm to pairs of numbers until you find the GCF of all the numbers.
Real-World Applications and Examples
Let's illustrate the practical application of the GCF with some real-world examples:
-
Baking: You are baking cookies and have 36 chocolate chips and 45 peanut butter chips. You want to divide the chips evenly among the cookies, ensuring each cookie has the same number of chocolate and peanut butter chips. The GCF (9) tells you that you can make 9 cookies, each with 4 chocolate chips and 5 peanut butter chips.
-
Gardening: You have a rectangular garden plot measuring 36 feet by 45 feet. You want to divide the garden into square plots of equal size without any leftover space. The GCF (9) indicates the largest possible square plot size is 9 feet by 9 feet.
-
Sharing Items: You have 36 pencils and 45 erasers to distribute evenly among students. The GCF (9) indicates you can give each student 4 pencils and 5 erasers.
Conclusion: Mastering the GCF
Understanding the GCF is a fundamental skill in mathematics with diverse applications across various fields. Whether you are simplifying fractions, solving equations, or tackling real-world problems involving equal distribution or size optimization, the GCF provides a crucial tool for finding efficient and elegant solutions. The methods discussed – listing factors, prime factorization, and the Euclidean algorithm – offer different approaches to finding the GCF, each with its own strengths and weaknesses. By mastering these methods and understanding the underlying concepts, you equip yourself with a powerful mathematical tool for tackling a wide range of challenges. The seemingly simple question of "What is the GCF of 36 and 45?" opens up a fascinating world of mathematical concepts and practical applications.
Latest Posts
Latest Posts
-
How Big Is 100 X 70 Cm
Aug 23, 2025
-
Why Did The Cow Give Only Buttermilk
Aug 23, 2025
-
How Do You Say Hazel In Spanish
Aug 23, 2025
-
How Far Is Chandler Arizona From Phoenix
Aug 23, 2025
-
What Is Five Percent Of One Million
Aug 23, 2025
Related Post
Thank you for visiting our website which covers about What Is The Gcf Of 36 And 45 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.