What Is The Gcf Of 45 And 60
Kalali
Aug 24, 2025 · 6 min read
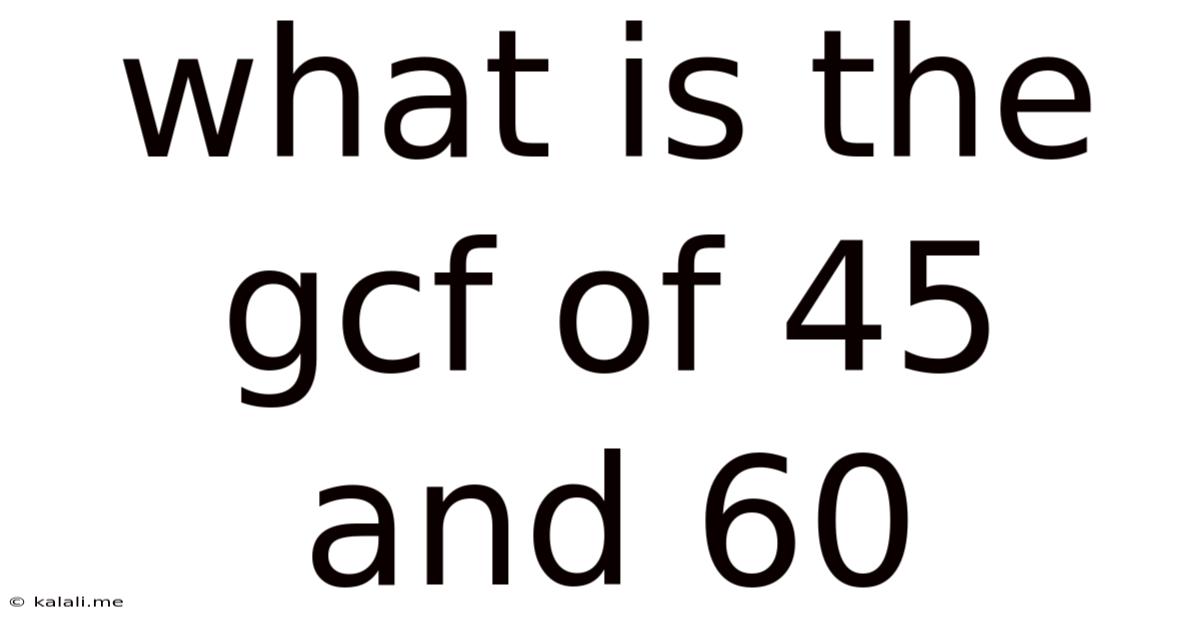
Table of Contents
Unveiling the GCF: A Deep Dive into Finding the Greatest Common Factor of 45 and 60
Finding the greatest common factor (GCF) of two numbers might seem like a simple arithmetic task, but understanding the underlying concepts and different methods for calculating it unlocks a deeper appreciation for number theory and its applications in various fields. This article will explore the GCF of 45 and 60 in detail, covering multiple approaches, demonstrating the practical applications, and delving into the related concepts of least common multiple (LCM) and prime factorization. This in-depth analysis aims to provide a comprehensive understanding of the topic, suitable for students, educators, and anyone interested in mathematics.
What is the Greatest Common Factor (GCF)?
The greatest common factor (GCF), also known as the greatest common divisor (GCD), is the largest number that divides exactly into two or more numbers without leaving a remainder. It represents the largest shared factor among the given numbers. In simpler terms, it's the biggest number that fits perfectly into all the numbers involved. Understanding the GCF is fundamental to simplifying fractions, solving algebraic equations, and working with geometric problems.
Methods for Finding the GCF of 45 and 60
Several methods can be used to determine the GCF of 45 and 60. We'll explore the most common and effective techniques:
1. Listing Factors:
This method involves listing all the factors of each number and then identifying the largest common factor.
- Factors of 45: 1, 3, 5, 9, 15, 45
- Factors of 60: 1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30, 60
Comparing the lists, we see that the common factors are 1, 3, 5, and 15. The greatest among these is 15. Therefore, the GCF of 45 and 60 is 15. While straightforward for smaller numbers, this method can become cumbersome with larger numbers.
2. Prime Factorization:
Prime factorization involves breaking down each number into its prime factors—numbers divisible only by 1 and themselves. This method is particularly efficient for larger numbers.
- Prime factorization of 45: 3 x 3 x 5 = 3² x 5
- Prime factorization of 60: 2 x 2 x 3 x 5 = 2² x 3 x 5
To find the GCF, identify the common prime factors and their lowest powers. Both 45 and 60 share a 3 and a 5. The lowest power of 3 is 3¹ (or simply 3), and the lowest power of 5 is 5¹. Multiplying these together gives us 3 x 5 = 15, confirming the GCF.
3. Euclidean Algorithm:
The Euclidean algorithm is a highly efficient method, especially for larger numbers. It uses successive divisions until the remainder is zero. The last non-zero remainder is the GCF.
- Divide the larger number (60) by the smaller number (45): 60 ÷ 45 = 1 with a remainder of 15.
- Replace the larger number with the smaller number (45) and the smaller number with the remainder (15).
- Repeat the division: 45 ÷ 15 = 3 with a remainder of 0.
- Since the remainder is 0, the GCF is the last non-zero remainder, which is 15.
The Euclidean algorithm is computationally efficient and avoids the need to list all factors, making it ideal for larger numbers where the listing method becomes impractical.
Applications of the Greatest Common Factor
Understanding and calculating the GCF has numerous practical applications across various fields:
-
Simplifying Fractions: The GCF is crucial for reducing fractions to their simplest form. For example, the fraction 45/60 can be simplified by dividing both the numerator and the denominator by their GCF, 15, resulting in the equivalent fraction 3/4.
-
Algebraic Expressions: The GCF helps in factoring algebraic expressions. For example, consider the expression 45x + 60y. The GCF of 45 and 60 is 15, so we can factor the expression as 15(3x + 4y).
-
Geometry: The GCF plays a role in solving geometric problems. For example, determining the largest square tile that can perfectly cover a rectangular area with dimensions 45 units and 60 units requires finding the GCF of 45 and 60, which is 15.
-
Number Theory: The GCF is a fundamental concept in number theory, used in various advanced mathematical proofs and theorems.
-
Computer Science: Algorithms for finding the GCF are employed in computer science for tasks such as cryptography and data compression.
Connecting GCF and LCM: The Relationship Between Two Key Concepts
The least common multiple (LCM) is another important concept related to the GCF. The LCM is the smallest number that is a multiple of both given numbers. There's a crucial relationship between the GCF and LCM:
For any two numbers 'a' and 'b', the product of their GCF and LCM is equal to the product of the two numbers themselves. Mathematically:
GCF(a, b) × LCM(a, b) = a × b
Using this relationship, we can calculate the LCM of 45 and 60, knowing their GCF is 15:
15 × LCM(45, 60) = 45 × 60 LCM(45, 60) = (45 × 60) / 15 = 180
Therefore, the LCM of 45 and 60 is 180. This relationship provides a convenient method for calculating the LCM once the GCF is known.
Expanding the Concept: GCF of More Than Two Numbers
The concept of GCF extends to finding the greatest common factor of more than two numbers. The methods discussed earlier can be adapted for this scenario. For example, let's find the GCF of 45, 60, and 75:
- Prime Factorization:
- 45 = 3² x 5
- 60 = 2² x 3 x 5
- 75 = 3 x 5²
The common prime factors are 3 and 5. The lowest powers are 3¹ and 5¹. Therefore, the GCF(45, 60, 75) = 3 x 5 = 15.
- Euclidean Algorithm (Adaptation): The Euclidean algorithm can be extended to multiple numbers by iteratively finding the GCF of pairs of numbers. First, find the GCF of 45 and 60 (which is 15). Then, find the GCF of 15 and 75 (which is 15). Thus, the GCF(45, 60, 75) = 15.
Conclusion: Mastering the GCF and its Applications
Understanding the greatest common factor is a fundamental skill in mathematics with wide-ranging applications. This article has explored various methods for calculating the GCF, highlighting their strengths and weaknesses. We've demonstrated the importance of the GCF in simplifying fractions, factoring algebraic expressions, solving geometric problems, and its connection to the least common multiple. By mastering these concepts and techniques, you'll enhance your mathematical problem-solving abilities and gain a deeper understanding of number theory. The ability to efficiently determine the GCF, whether using prime factorization or the Euclidean algorithm, is a valuable asset in various mathematical and computational contexts. Remember, the seemingly simple task of finding the GCF of 45 and 60 opens doors to a much broader understanding of mathematical principles and their practical relevance.
Latest Posts
Latest Posts
-
How Much Should A 5th Grader Weigh
Aug 25, 2025
-
Songs From Madea One Big Happy Family
Aug 25, 2025
-
What Satan Meant For Evil Bible Verse
Aug 25, 2025
-
What Animals Eyes Glow Orange At Night
Aug 25, 2025
-
How Many Feet Are In 24 Yards
Aug 25, 2025
Related Post
Thank you for visiting our website which covers about What Is The Gcf Of 45 And 60 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.