What Is The Gcf Of 81 And 72
Kalali
Aug 22, 2025 · 6 min read
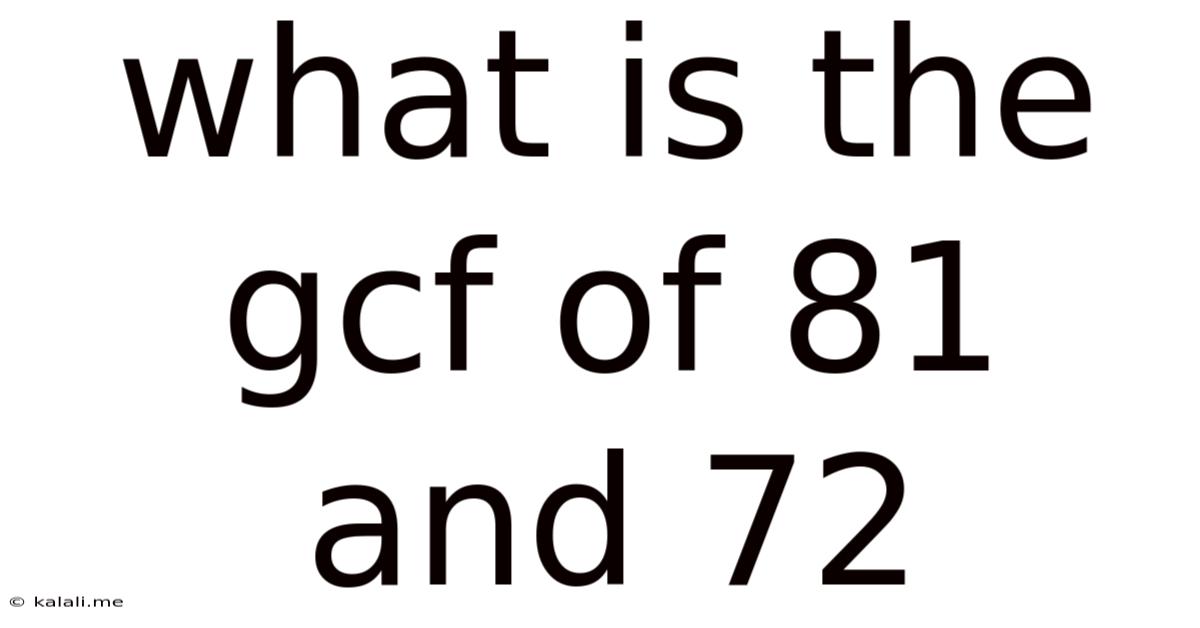
Table of Contents
What is the GCF of 81 and 72? A Deep Dive into Finding the Greatest Common Factor
Finding the greatest common factor (GCF) of two numbers might seem like a simple arithmetic problem, but understanding the underlying concepts and different methods for solving it opens up a world of mathematical understanding, useful in various applications beyond basic arithmetic. This article explores multiple ways to find the GCF of 81 and 72, delving into the theory behind the methods, their practical applications, and related mathematical concepts. We'll also explore why understanding GCF is crucial, not just for academic purposes, but also for real-world problem-solving. The meta description for this article is: Learn how to find the greatest common factor (GCF) of 81 and 72 using various methods, including prime factorization and the Euclidean algorithm. Discover practical applications and related mathematical concepts.
Understanding the Greatest Common Factor (GCF)
Before we dive into finding the GCF of 81 and 72, let's define what the GCF actually is. The greatest common factor (GCF), also known as the greatest common divisor (GCD), is the largest positive integer that divides each of the integers without leaving a remainder. In simpler terms, it's the biggest number that goes evenly into both numbers. This concept is fundamental in number theory and has widespread applications in various fields, including algebra, geometry, and computer science. Finding the GCF is a crucial step in simplifying fractions, solving equations, and understanding the relationships between numbers.
Method 1: Prime Factorization
The prime factorization method is a classic and intuitive approach to finding the GCF. It involves breaking down each number into its prime factors – numbers divisible only by 1 and themselves. Let's apply this method to find the GCF of 81 and 72:
1. Prime Factorization of 81:
81 can be factored as follows:
- 81 = 3 x 27
- 81 = 3 x 3 x 9
- 81 = 3 x 3 x 3 x 3 or 3<sup>4</sup>
2. Prime Factorization of 72:
72 can be factored as follows:
- 72 = 2 x 36
- 72 = 2 x 2 x 18
- 72 = 2 x 2 x 2 x 9
- 72 = 2 x 2 x 2 x 3 x 3 or 2<sup>3</sup> x 3<sup>2</sup>
3. Identifying Common Factors:
Now, let's compare the prime factorizations of 81 and 72:
81 = 3<sup>4</sup> 72 = 2<sup>3</sup> x 3<sup>2</sup>
The common prime factor is 3. The lowest power of 3 present in both factorizations is 3².
4. Calculating the GCF:
The GCF is the product of the common prime factors raised to their lowest power. In this case, the GCF of 81 and 72 is 3² = 9.
Therefore, the greatest common factor of 81 and 72 is 9.
Method 2: Listing Factors
This method is straightforward, particularly useful for smaller numbers. We list all the factors of each number and identify the largest factor common to both.
1. Factors of 81: 1, 3, 9, 27, 81
2. Factors of 72: 1, 2, 3, 4, 6, 8, 9, 12, 18, 24, 36, 72
3. Common Factors: Comparing the two lists, we find the common factors are 1, 3, and 9.
4. Greatest Common Factor: The largest common factor is 9.
This method is less efficient for larger numbers, as listing all factors becomes time-consuming. The prime factorization method is generally preferred for larger numbers.
Method 3: Euclidean Algorithm
The Euclidean algorithm is a highly efficient method for finding the GCF, especially for larger numbers. It's based on the principle that the GCF of two numbers doesn't change if the larger number is replaced by its difference with the smaller number. This process is repeated until the two numbers are equal, and that number is the GCF.
Let's apply the Euclidean algorithm to find the GCF of 81 and 72:
-
Start with the larger number (81) and the smaller number (72): 81, 72
-
Subtract the smaller number from the larger number: 81 - 72 = 9
-
Replace the larger number with the result (9) and repeat the process: 72, 9
-
Subtract the smaller number from the larger number: 72 - (9 x 8) = 0
Since the remainder is 0, the GCF is the last non-zero remainder, which is 9.
The Euclidean algorithm provides a systematic and efficient way to find the GCF, especially when dealing with large numbers where prime factorization might be cumbersome.
Real-World Applications of GCF
Understanding and calculating the GCF has numerous practical applications beyond the classroom:
-
Simplifying Fractions: Finding the GCF is crucial for simplifying fractions to their lowest terms. For example, the fraction 72/81 can be simplified to 8/9 by dividing both the numerator and denominator by their GCF, which is 9.
-
Geometry: GCF is used in solving geometric problems involving the dimensions of shapes. For instance, finding the largest square tile that can perfectly cover a rectangular floor with dimensions 72 inches by 81 inches requires calculating the GCF of 72 and 81.
-
Measurement and Division: Determining the largest possible equal units for dividing quantities relies on calculating the GCF. Imagine dividing 81 apples and 72 oranges into equal groups; the GCF (9) helps determine the maximum number of identical groups possible.
-
Project Management: In project management, determining the optimal scheduling or resource allocation often benefits from calculating the GCF of task durations or resource quantities.
-
Computer Science: The Euclidean algorithm, used for finding the GCF, is a fundamental algorithm in computer science, used in cryptography and other computational tasks.
Beyond the GCF: Least Common Multiple (LCM)
Closely related to the GCF is the least common multiple (LCM). The LCM of two numbers is the smallest positive integer that is divisible by both numbers. While the GCF represents the largest common divisor, the LCM represents the smallest common multiple. The GCF and LCM are connected through the following formula:
LCM(a, b) x GCF(a, b) = a x b
Using this formula, we can calculate the LCM of 81 and 72:
LCM(81, 72) = (81 x 72) / GCF(81, 72) = (81 x 72) / 9 = 648
Therefore, the least common multiple of 81 and 72 is 648. The LCM is particularly useful in situations requiring finding the smallest common denominator when adding or subtracting fractions.
Conclusion: Mastering GCF for Mathematical Proficiency
Finding the greatest common factor of 81 and 72, as demonstrated through various methods, is more than just a simple arithmetic exercise. It's a gateway to understanding fundamental concepts in number theory with wide-ranging applications in various fields. Mastering these methods, particularly the Euclidean algorithm for larger numbers, enhances mathematical proficiency and problem-solving skills. The connection between the GCF and LCM further underscores the interconnectedness of mathematical concepts and their importance in tackling real-world challenges. By understanding the underlying principles and utilizing the most efficient methods, you can confidently tackle GCF problems and appreciate its significance in various mathematical and practical contexts.
Latest Posts
Latest Posts
-
How Long Is 300 Miles In Hours
Aug 22, 2025
-
When Does Ichigo Learn About His Dad
Aug 22, 2025
-
How Do You Say Mine In Spanish
Aug 22, 2025
-
How Many 4x8 Bricks In A Square Foot
Aug 22, 2025
-
How Much Does A Bar Weigh Without Weights
Aug 22, 2025
Related Post
Thank you for visiting our website which covers about What Is The Gcf Of 81 And 72 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.