What Is The Greatest Common Factor Of 16 And 28
Kalali
Aug 23, 2025 · 5 min read
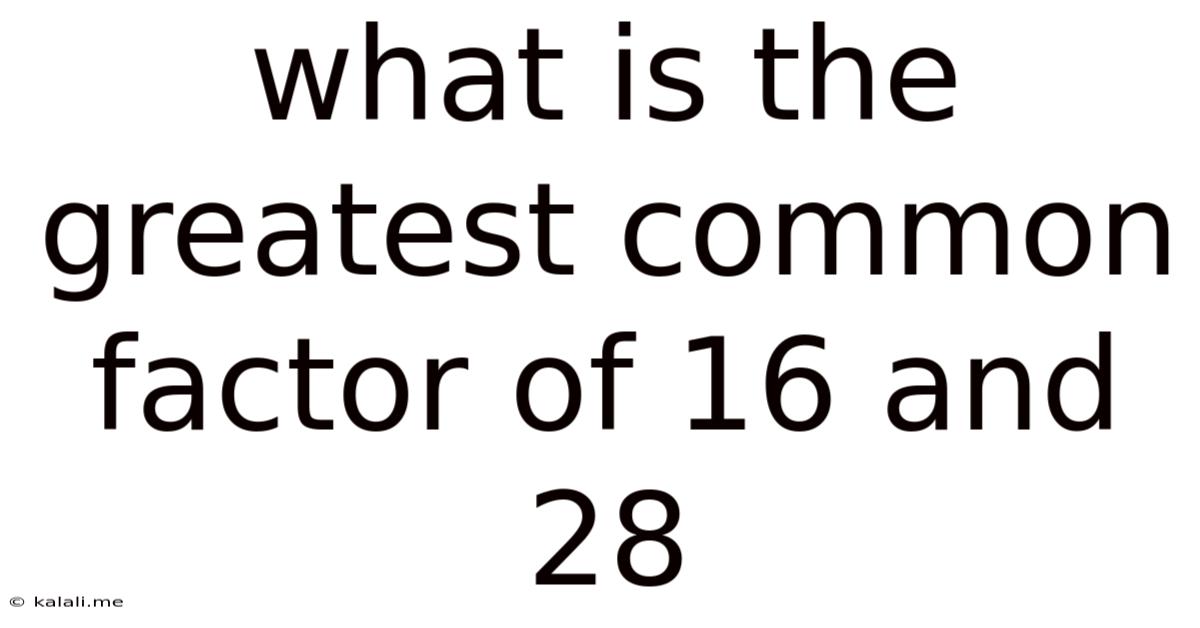
Table of Contents
Unveiling the Greatest Common Factor (GCF) of 16 and 28: A Deep Dive into Number Theory
Finding the greatest common factor (GCF), also known as the greatest common divisor (GCD), of two numbers might seem like a simple arithmetic problem. However, understanding the underlying concepts and exploring different methods for solving it opens up a fascinating world of number theory with practical applications in various fields. This article will delve into the GCF of 16 and 28, demonstrating multiple approaches and explaining the broader mathematical principles involved. We'll also explore the significance of GCF in areas beyond basic arithmetic.
What is the Greatest Common Factor (GCF)?
The greatest common factor (GCF) of two or more integers is the largest positive integer that divides each of the integers without leaving a remainder. In simpler terms, it's the biggest number that goes into both numbers evenly. For example, the GCF of 12 and 18 is 6, because 6 is the largest number that divides both 12 and 18 without leaving a remainder.
Finding the GCF of 16 and 28: Multiple Methods
Let's now focus on finding the GCF of 16 and 28. We'll explore several methods, each offering a unique perspective on this fundamental concept.
1. Listing Factors Method:
This is the most straightforward method, especially for smaller numbers. We list all the factors of each number and then identify the largest factor they share.
- Factors of 16: 1, 2, 4, 8, 16
- Factors of 28: 1, 2, 4, 7, 14, 28
Comparing the two lists, we see that the common factors are 1, 2, and 4. The largest of these is 4. Therefore, the GCF of 16 and 28 is 4.
2. Prime Factorization Method:
This method utilizes the fundamental theorem of arithmetic, which states that every integer greater than 1 can be uniquely represented as a product of prime numbers. Prime numbers are numbers greater than 1 that are only divisible by 1 and themselves (e.g., 2, 3, 5, 7, 11...).
- Prime factorization of 16: 2 x 2 x 2 x 2 = 2⁴
- Prime factorization of 28: 2 x 2 x 7 = 2² x 7
To find the GCF, we identify the common prime factors and their lowest powers. Both 16 and 28 share two factors of 2 (2²). Therefore, the GCF is 2² = 4.
3. Euclidean Algorithm:
The Euclidean algorithm is a highly efficient method for finding the GCF of two integers, especially for larger numbers. It's based on the principle that the GCF of two numbers does not change if the larger number is replaced by its difference with the smaller number. This process is repeated until the two numbers are equal, and that number is the GCF.
Let's apply the Euclidean algorithm to 16 and 28:
- 28 = 16 x 1 + 12 (Subtract 16 from 28)
- 16 = 12 x 1 + 4 (Subtract 12 from 16)
- 12 = 4 x 3 + 0 (Subtract multiples of 4 from 12 until remainder is 0)
The last non-zero remainder is 4, which is the GCF of 16 and 28.
4. Ladder Method (Staircase Method):
The ladder method is a visual representation of the Euclidean algorithm. It’s particularly helpful for demonstrating the step-by-step process.
28 | 16
12 | 2
4 |
We start by dividing the larger number (28) by the smaller number (16). The remainder (12) becomes the new divisor, and the previous divisor (16) becomes the new dividend. We repeat this process until the remainder is 0. The last non-zero remainder (4) is the GCF.
The Significance of GCF Beyond Basic Arithmetic
While finding the GCF might seem like a purely mathematical exercise, it has significant applications in various fields:
-
Simplification of Fractions: The GCF is crucial for simplifying fractions to their lowest terms. For example, the fraction 16/28 can be simplified to 4/7 by dividing both the numerator and the denominator by their GCF (4).
-
Solving Problems Involving Ratios and Proportions: GCF helps in simplifying ratios and proportions, making them easier to understand and work with.
-
Geometry and Measurement: GCF is used in geometric problems involving finding the dimensions of rectangles or other shapes with integer sides. For instance, if you need to cut squares of equal size from a rectangular piece of material (16 units by 28 units), the side length of the largest possible squares will be the GCF of 16 and 28 (4 units).
-
Cryptography: Concepts related to GCF, particularly the Euclidean algorithm, are fundamental in modern cryptography, playing a vital role in algorithms like RSA encryption.
-
Computer Science: GCF calculations are frequently used in computer algorithms for various tasks, such as optimizing data structures and simplifying computations.
-
Music Theory: The GCF can help determine the greatest common divisor of musical intervals, which is relevant in understanding harmonic relationships.
Conclusion: Understanding the Power of the GCF
The seemingly simple task of finding the greatest common factor of 16 and 28, as we've demonstrated, unlocks a deeper understanding of number theory and its wide-ranging applications. From simplifying fractions to securing sensitive data, the GCF plays a significant role in various disciplines. Mastering different methods for calculating the GCF, such as the listing factors method, prime factorization, Euclidean algorithm, and the ladder method, equips you with valuable tools for tackling mathematical problems and appreciating the elegance of number theory. The GCF is not just a simple arithmetic concept; it's a foundational element in many advanced mathematical and computational processes. The answer, consistently found through all methods, remains definitively 4.
Latest Posts
Latest Posts
-
How Fast Can A 90cc Atv Go
Aug 23, 2025
-
What Is The Best Example Of A Narrative
Aug 23, 2025
-
Can A Decimal Be A Natural Number
Aug 23, 2025
-
How Far Will A 380 Bullet Travel
Aug 23, 2025
-
How Many Ml Is A Coke Can
Aug 23, 2025
Related Post
Thank you for visiting our website which covers about What Is The Greatest Common Factor Of 16 And 28 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.