What Is The Greatest Common Factor Of 30 And 54
Kalali
Jul 15, 2025 · 5 min read
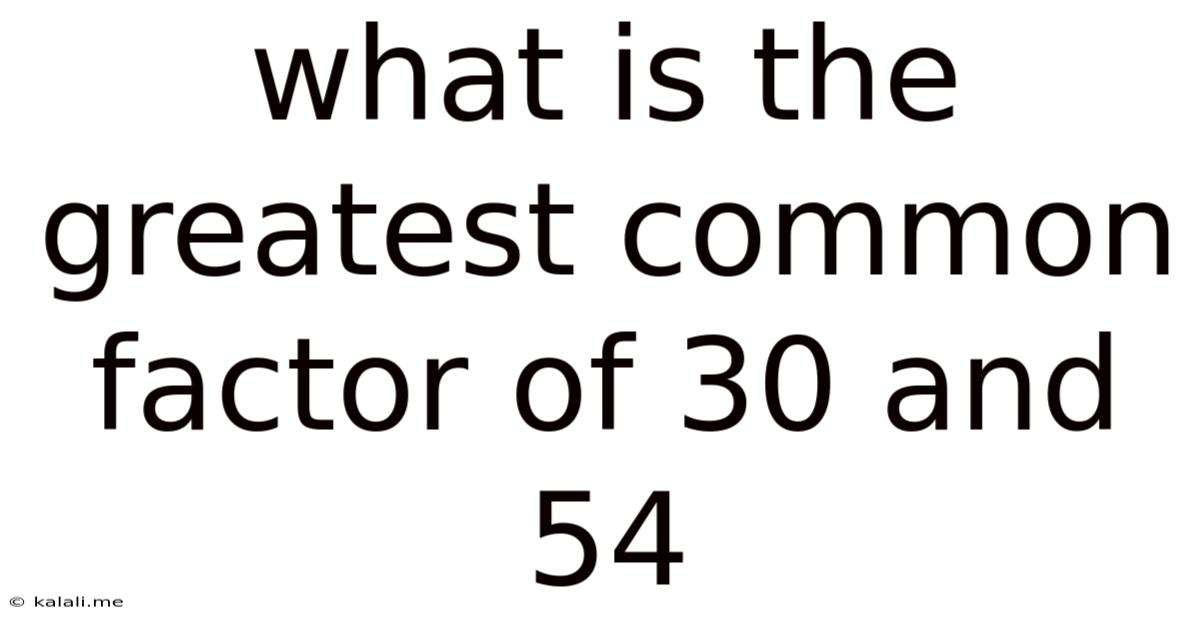
Table of Contents
Unlocking the Secrets of the Greatest Common Factor: A Deep Dive into 30 and 54
Finding the greatest common factor (GCF) might seem like a simple arithmetic task, but understanding the underlying principles unlocks a deeper appreciation for number theory and its applications in various fields. This article will delve into the fascinating world of GCFs, specifically focusing on the GCF of 30 and 54, while exploring various methods for calculating it and highlighting its significance in mathematics and beyond. We'll move beyond simply stating the answer to explore the "why" and "how" behind the calculations, making this more than just a simple math problem; it's an exploration of mathematical concepts.
What is the Greatest Common Factor (GCF)?
The greatest common factor (GCF), also known as the greatest common divisor (GCD), is the largest positive integer that divides each of the integers without leaving a remainder. In simpler terms, it's the biggest number that can perfectly divide both numbers. Understanding the GCF is crucial in simplifying fractions, solving algebraic equations, and understanding various mathematical relationships.
Methods for Finding the GCF of 30 and 54
Several methods exist for determining the GCF of two numbers. Let's explore the most common approaches, applying them to find the GCF of 30 and 54:
1. Listing Factors:
This is a straightforward method, especially useful for smaller numbers. We list all the factors of each number and then identify the largest factor common to both.
- Factors of 30: 1, 2, 3, 5, 6, 10, 15, 30
- Factors of 54: 1, 2, 3, 6, 9, 18, 27, 54
Comparing the lists, we see that the common factors are 1, 2, 3, and 6. The greatest among these is 6. Therefore, the GCF of 30 and 54 is 6.
2. Prime Factorization:
This method involves breaking down each number into its prime factors. The GCF is then found by multiplying the common prime factors raised to the lowest power.
- Prime factorization of 30: 2 × 3 × 5
- Prime factorization of 54: 2 × 3 × 3 × 3 = 2 × 3³
The common prime factors are 2 and 3. The lowest power of 2 is 2¹ and the lowest power of 3 is 3¹. Multiplying these together: 2 × 3 = 6. Therefore, the GCF of 30 and 54 is 6. This method is particularly efficient for larger numbers.
3. Euclidean Algorithm:
This is a highly efficient algorithm for finding the GCF, especially for larger numbers. It's based on the principle that the GCF of two numbers doesn't change if the larger number is replaced by its difference with the smaller number. We repeatedly apply this process until we reach a point where the remainder is 0. The last non-zero remainder is the GCF.
Let's apply the Euclidean Algorithm to 30 and 54:
- 54 = 30 × 1 + 24
- 30 = 24 × 1 + 6
- 24 = 6 × 4 + 0
The last non-zero remainder is 6. Therefore, the GCF of 30 and 54 is 6. The Euclidean algorithm is computationally efficient and is often preferred for larger numbers where listing factors or prime factorization become cumbersome.
Significance of the GCF
The GCF has numerous applications across various mathematical fields and real-world scenarios:
-
Simplifying Fractions: The GCF allows us to simplify fractions to their lowest terms. For instance, the fraction 30/54 can be simplified by dividing both the numerator and denominator by their GCF, 6, resulting in the equivalent fraction 5/9.
-
Solving Equations: The GCF plays a critical role in solving Diophantine equations, which are equations where solutions are restricted to integers.
-
Geometry: The GCF is used in geometric problems involving the dimensions of shapes. For example, finding the largest square tile that can perfectly cover a rectangular floor requires calculating the GCF of the floor's length and width.
-
Modular Arithmetic: In cryptography and computer science, the GCF is essential in modular arithmetic operations.
-
Abstract Algebra: The concept extends into abstract algebra, where it finds applications in ring theory and ideal theory.
Beyond the Basics: Exploring Related Concepts
Understanding the GCF opens doors to exploring related concepts in number theory:
-
Least Common Multiple (LCM): The LCM is the smallest positive integer that is a multiple of both numbers. The relationship between GCF and LCM is given by the formula: GCF(a, b) × LCM(a, b) = a × b. For 30 and 54, the LCM is 270.
-
Coprime Numbers: Two numbers are coprime (or relatively prime) if their GCF is 1. This concept is crucial in number theory and cryptography.
-
Divisibility Rules: Understanding divisibility rules can help quickly determine if a number is divisible by another, aiding in the process of finding factors and GCF.
Practical Applications and Real-World Examples:
The GCF isn't just a theoretical concept; it has practical applications in everyday life:
-
Baking: If you have 30 apples and 54 oranges, and you want to divide them into identical bags with the largest possible number of fruits in each bag, you would use the GCF (6) to determine that you can create 6 bags, each containing 5 apples and 9 oranges.
-
Construction: Imagine you're tiling a rectangular area with square tiles. Finding the GCF of the length and width of the area helps determine the largest possible size of the square tiles that can perfectly cover the area without any cutting or gaps.
-
Resource Allocation: Distributing resources fairly among groups often involves using the GCF to ensure equal distribution.
Conclusion:
Finding the greatest common factor of 30 and 54, which is 6, is more than just a simple arithmetic exercise. It's a gateway to understanding fundamental concepts in number theory with wide-ranging applications in mathematics, computer science, and everyday life. By exploring different methods for calculating the GCF and understanding its significance, we gain a deeper appreciation for the interconnectedness of mathematical ideas and their practical relevance. The seemingly simple act of finding the GCF reveals a rich tapestry of mathematical relationships, demonstrating the power and elegance of number theory. From simplifying fractions to solving complex equations, the GCF proves to be a crucial tool in the mathematician's arsenal.
Latest Posts
Latest Posts
-
How Many Oz In A Pint Of Tomatoes
Jul 15, 2025
-
How Long Does Condensed Milk Last In The Fridge
Jul 15, 2025
-
How Many Degrees Is A Straight Line
Jul 15, 2025
-
How Many Seconds Are In A Lifetime
Jul 15, 2025
-
List Of 4 Digit Combinations 1 9 No Repeats
Jul 15, 2025
Related Post
Thank you for visiting our website which covers about What Is The Greatest Common Factor Of 30 And 54 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.