What Is The Greatest Common Factor Of 35 And 21
Kalali
Jul 27, 2025 · 6 min read
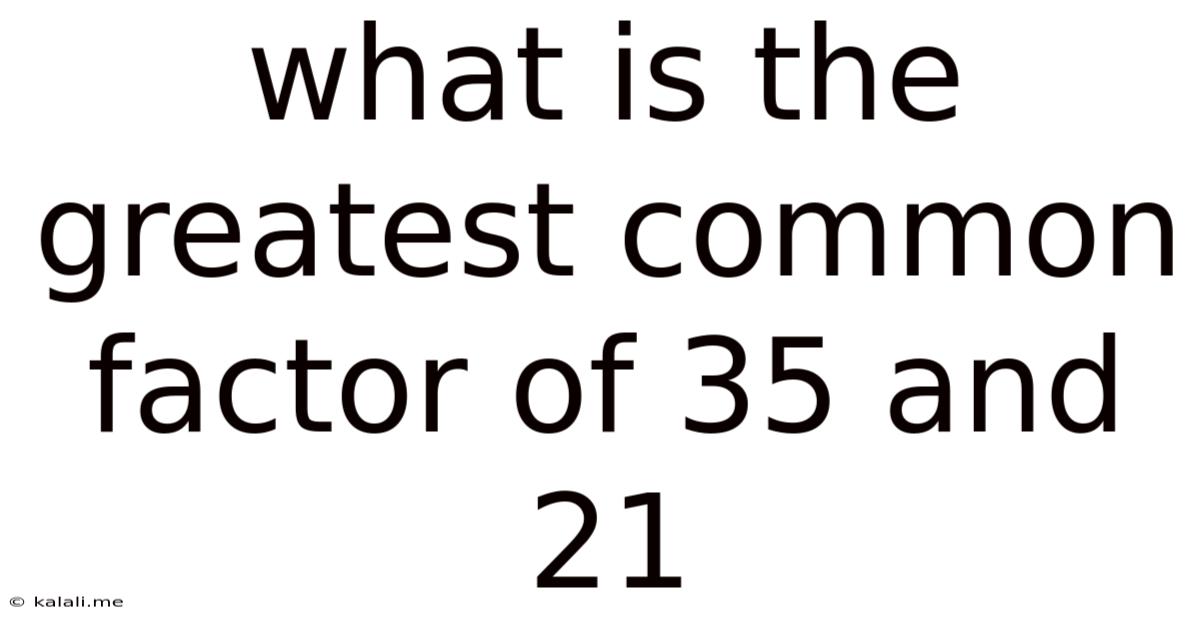
Table of Contents
Unveiling the Greatest Common Factor (GCF) of 35 and 21: A Deep Dive into Number Theory
Finding the greatest common factor (GCF) of two numbers might seem like a simple arithmetic task, suitable only for elementary school students. However, understanding the concept of GCF extends far beyond basic calculations. It's a fundamental concept in number theory with applications in various fields, from cryptography to computer science. This article will delve into the methods of finding the GCF of 35 and 21, exploring different approaches and highlighting the broader significance of this mathematical concept. We'll move beyond simply stating the answer and explore the underlying principles, providing a comprehensive understanding for both beginners and those seeking a refresher.
Meta Description: Discover the greatest common factor (GCF) of 35 and 21 using various methods. Learn about prime factorization, the Euclidean algorithm, and the significance of GCF in number theory and its applications. This comprehensive guide explores the concept beyond simple calculation.
Understanding the Greatest Common Factor (GCF)
Before we tackle the specific problem of finding the GCF of 35 and 21, let's define what a greatest common factor actually is. The GCF, also known as the greatest common divisor (GCD), is the largest positive integer that divides each of the integers without leaving a remainder. In simpler terms, it's the biggest number that perfectly divides both numbers. For example, the factors of 12 are 1, 2, 3, 4, 6, and 12. The factors of 18 are 1, 2, 3, 6, 9, and 18. The common factors of 12 and 18 are 1, 2, 3, and 6. Therefore, the greatest common factor of 12 and 18 is 6.
Finding the GCF is crucial in various mathematical operations, particularly when simplifying fractions and solving algebraic equations. It's a building block for more advanced concepts in number theory and algebra.
Method 1: Prime Factorization
One of the most common methods for determining the GCF is through prime factorization. This method involves breaking down each number into its prime factors – numbers divisible only by 1 and themselves.
Let's apply this method to find the GCF of 35 and 21:
- Prime factorization of 35: 35 = 5 x 7
- Prime factorization of 21: 21 = 3 x 7
Once we have the prime factorization of both numbers, we identify the common prime factors. In this case, both 35 and 21 share the prime factor 7. The GCF is the product of these common prime factors. Therefore, the GCF of 35 and 21 is 7.
Method 2: The Euclidean Algorithm
The Euclidean algorithm provides a more efficient method for finding the GCF, especially when dealing with larger numbers. This algorithm is based on the principle that the GCF of two numbers does not change if the larger number is replaced by its difference with the smaller number. This process is repeated until the two numbers are equal, and that number is the GCF.
Let's apply the Euclidean algorithm to find the GCF of 35 and 21:
- Start with the larger number (35) and the smaller number (21).
- Subtract the smaller number from the larger number: 35 - 21 = 14
- Replace the larger number with the result (14) and repeat the process: 21 - 14 = 7
- Repeat: 14 - 7 = 7
- The process stops when the result is 0. The GCF is the last non-zero remainder, which is 7.
Method 3: Listing Factors
A simpler, albeit less efficient for larger numbers, method involves listing all the factors of each number and identifying the greatest common factor.
- Factors of 35: 1, 5, 7, 35
- Factors of 21: 1, 3, 7, 21
By comparing the lists, we can see that the common factors are 1 and 7. The greatest of these common factors is 7. Therefore, the GCF of 35 and 21 is 7.
Applications of the Greatest Common Factor
The GCF has numerous applications across various fields:
-
Simplifying Fractions: The GCF is used to simplify fractions to their lowest terms. For example, the fraction 35/21 can be simplified by dividing both the numerator and denominator by their GCF, which is 7. This results in the simplified fraction 5/3.
-
Solving Algebraic Equations: The GCF is essential in factoring algebraic expressions. Factoring allows us to solve equations more easily and understand the structure of polynomials.
-
Cryptography: The GCF plays a critical role in cryptographic algorithms, such as the RSA algorithm, which is widely used for secure data transmission.
-
Computer Science: The GCF is used in various computer science algorithms, such as finding the least common multiple (LCM) of two numbers, which is closely related to the GCF. The LCM is used in scheduling tasks and managing resources in computer systems.
-
Geometry: The GCF can be used to solve problems related to geometric shapes, such as finding the dimensions of the largest square that can be used to tile a rectangle. This involves finding the GCF of the rectangle's length and width.
-
Music Theory: The concept of GCF finds application in music theory, specifically in determining the greatest common divisor of musical intervals. This helps in understanding harmonic relationships between notes.
Beyond the Basics: Exploring Related Concepts
Understanding the GCF opens doors to related and more advanced mathematical concepts:
-
Least Common Multiple (LCM): The LCM is the smallest positive integer that is a multiple of both numbers. The GCF and LCM are intimately related; their product is equal to the product of the two original numbers (GCF x LCM = number1 x number2).
-
Modular Arithmetic: This branch of number theory deals with remainders after division. The GCF is a fundamental concept in understanding modular arithmetic and its applications in cryptography.
-
Diophantine Equations: These are algebraic equations where only integer solutions are sought. The GCF often plays a crucial role in determining the solvability and finding the solutions of Diophantine equations.
Conclusion: The Enduring Significance of the GCF
While finding the GCF of 35 and 21 might appear straightforward, the underlying principles and applications of this concept extend far beyond basic arithmetic. This seemingly simple calculation serves as a cornerstone for numerous mathematical fields, showcasing the power and elegance of number theory. Mastering the GCF isn't just about finding the answer; it's about understanding the fundamental concepts that underpin a vast array of mathematical and computational problems. From simplifying fractions to securing online transactions, the GCF is a fundamental concept with far-reaching implications. Understanding its various methods of calculation and its diverse applications provides a deeper appreciation for the beauty and utility of mathematics. Therefore, the seemingly simple answer – 7 – represents far more than just a numerical result; it represents a gateway to a deeper understanding of the interconnectedness of mathematical concepts.
Latest Posts
Latest Posts
-
What Does Ditto Mean In A Text Message
Jul 27, 2025
-
How Many Pounds Are In 8 Tons
Jul 27, 2025
-
One Pound Of Strawberries Is How Many Cups
Jul 27, 2025
-
How Much Was A Gallon Of Milk In 1902
Jul 27, 2025
-
Math Words That Start With J 8th Grade
Jul 27, 2025
Related Post
Thank you for visiting our website which covers about What Is The Greatest Common Factor Of 35 And 21 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.