What Is The Highest Common Factor Of 18 And 27
Kalali
Jul 19, 2025 · 6 min read
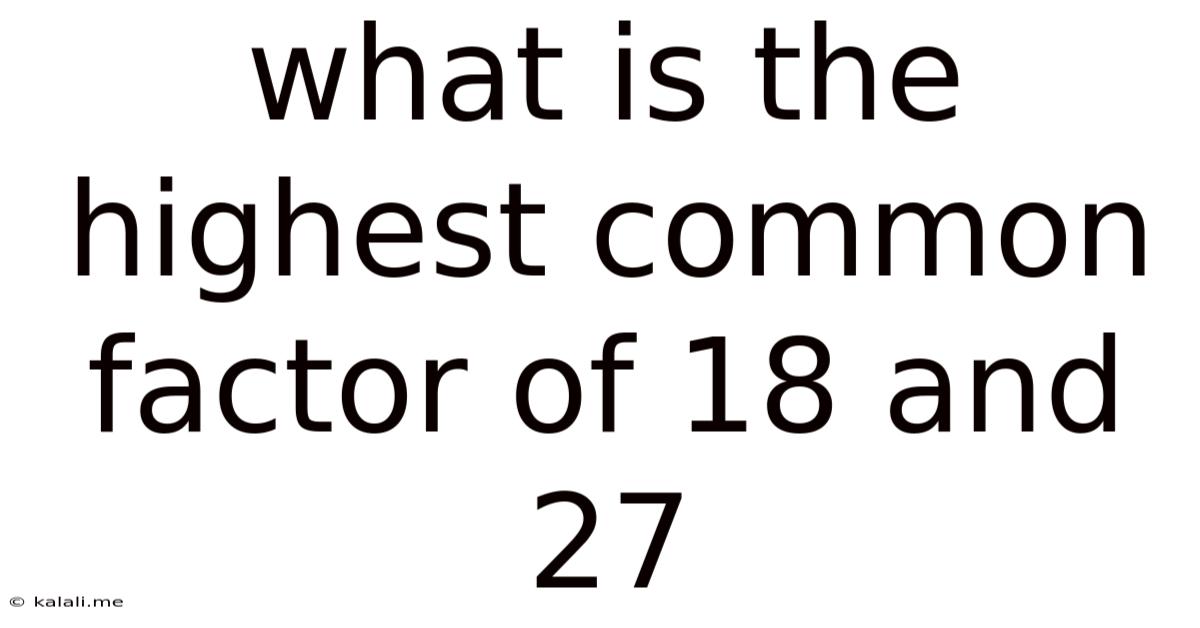
Table of Contents
Unlocking the Secrets of the Highest Common Factor: A Deep Dive into 18 and 27
Finding the Highest Common Factor (HCF), also known as the Greatest Common Divisor (GCD), might seem like a simple arithmetic problem. However, understanding the underlying concepts and exploring different methods to solve it reveals a fascinating journey into number theory. This article will delve deep into determining the HCF of 18 and 27, exploring various techniques, illustrating their applications, and showcasing the broader significance of HCF in mathematics and beyond. This detailed exploration will equip you with a comprehensive understanding, exceeding the typical explanation, ensuring you master this fundamental concept.
Meta Description: Discover the highest common factor of 18 and 27 through various methods, from prime factorization to the Euclidean algorithm. Learn the underlying principles and practical applications of HCF in mathematics and beyond. This comprehensive guide will take you beyond a simple answer, exploring the rich theory behind this fundamental concept.
What is the Highest Common Factor (HCF)?
The highest common factor (HCF) of two or more numbers is the largest number that divides each of them without leaving a remainder. In simpler terms, it's the biggest number that is a factor of all the given numbers. For example, the factors of 12 are 1, 2, 3, 4, 6, and 12. The factors of 18 are 1, 2, 3, 6, 9, and 18. The common factors of 12 and 18 are 1, 2, 3, and 6. Therefore, the highest common factor of 12 and 18 is 6.
Understanding the HCF is crucial in various mathematical operations and real-world applications, from simplifying fractions to solving problems involving proportions and ratios. Its applications extend beyond basic arithmetic, finding its use in areas like cryptography and computer science.
Finding the HCF of 18 and 27: Method 1 – Prime Factorization
The prime factorization method involves breaking down each number into its prime factors – numbers divisible only by 1 and themselves. This method provides a clear visual representation of the common factors.
1. Prime Factorization of 18:
18 can be broken down as follows:
18 = 2 x 9 = 2 x 3 x 3 = 2 x 3²
2. Prime Factorization of 27:
27 can be broken down as follows:
27 = 3 x 9 = 3 x 3 x 3 = 3³
3. Identifying Common Factors:
Comparing the prime factorizations of 18 and 27, we see that they share three factors of 3.
18 = 2 x 3² 27 = 3³
4. Calculating the HCF:
The HCF is the product of the common prime factors raised to the lowest power. In this case, the only common prime factor is 3, and the lowest power is 3¹. Therefore:
HCF(18, 27) = 3² = 9
Therefore, the highest common factor of 18 and 27 is 9.
Finding the HCF of 18 and 27: Method 2 – Listing Factors
This method involves listing all the factors of each number and then identifying the common factors. While straightforward for smaller numbers, it becomes less efficient for larger numbers.
1. Factors of 18: 1, 2, 3, 6, 9, 18
2. Factors of 27: 1, 3, 9, 27
3. Common Factors: 1, 3, 9
4. Highest Common Factor: The highest number among the common factors is 9.
Therefore, the highest common factor of 18 and 27 is 9.
Finding the HCF of 18 and 27: Method 3 – Euclidean Algorithm
The Euclidean algorithm is a highly efficient method for finding the HCF, especially for larger numbers. It’s based on the principle that the HCF of two numbers does not change if the larger number is replaced by its difference with the smaller number. This process is repeated until the two numbers are equal, and that number is the HCF.
1. Applying the Algorithm:
- Start with the larger number (27) and the smaller number (18).
- Subtract the smaller number from the larger number: 27 - 18 = 9
- Now, we have the numbers 18 and 9.
- Repeat the process: 18 - 9 = 9
- We now have the numbers 9 and 9. Since the numbers are equal, the HCF is 9.
Therefore, the highest common factor of 18 and 27 is 9.
Applications of HCF
The HCF has numerous applications across various fields:
-
Simplifying Fractions: The HCF helps simplify fractions to their lowest terms. For example, the fraction 18/27 can be simplified by dividing both the numerator and the denominator by their HCF (9), resulting in the simplified fraction 2/3.
-
Solving Word Problems: Many word problems involving sharing or grouping items equally require the use of HCF to find the largest possible group size or the maximum number of items that can be divided equally.
-
Geometry: HCF finds applications in geometric problems, particularly those involving measurements and divisions of shapes. For instance, finding the dimensions of the largest square tile that can perfectly cover a rectangular floor uses the HCF of the floor's length and width.
-
Cryptography: In cryptography, the HCF plays a vital role in algorithms like the RSA algorithm, which is widely used for secure data transmission.
-
Computer Science: HCF is essential in various computer algorithms and data structures, including those related to data compression and efficient data storage.
Beyond the Basics: Extending the Concept
While we’ve focused on finding the HCF of two numbers, the concept extends to finding the HCF of more than two numbers. The same methods – prime factorization and the Euclidean algorithm – can be adapted to handle multiple numbers. For example, to find the HCF of 18, 27, and 36, you would first find the HCF of any two numbers (say 18 and 27, which is 9), and then find the HCF of the result (9) and the remaining number (36). In this case, the HCF(18, 27, 36) would be 9.
The concept of the HCF is also closely related to the Least Common Multiple (LCM). The LCM is the smallest number that is a multiple of all the given numbers. The HCF and LCM are related by the following formula for two numbers a and b:
HCF(a, b) x LCM(a, b) = a x b
This relationship provides a powerful tool for solving problems involving both HCF and LCM.
Conclusion: Mastering the HCF
Finding the HCF of 18 and 27, as demonstrated through multiple methods, illustrates the fundamental concept and its practical applications. While seemingly straightforward for these small numbers, the underlying principles and techniques, particularly the Euclidean algorithm, prove invaluable when dealing with larger or multiple numbers. Understanding the HCF is not just about getting the right answer; it’s about grasping the core principles of number theory and their wide-ranging applications in mathematics, computer science, and beyond. This deep dive into the subject allows for a more comprehensive understanding and appreciation of this essential mathematical concept. The ability to efficiently and accurately calculate the HCF is a valuable skill applicable in diverse fields, making it a cornerstone of mathematical proficiency.
Latest Posts
Related Post
Thank you for visiting our website which covers about What Is The Highest Common Factor Of 18 And 27 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.