What Is The Lcm For 10 And 8
Kalali
Apr 11, 2025 · 6 min read
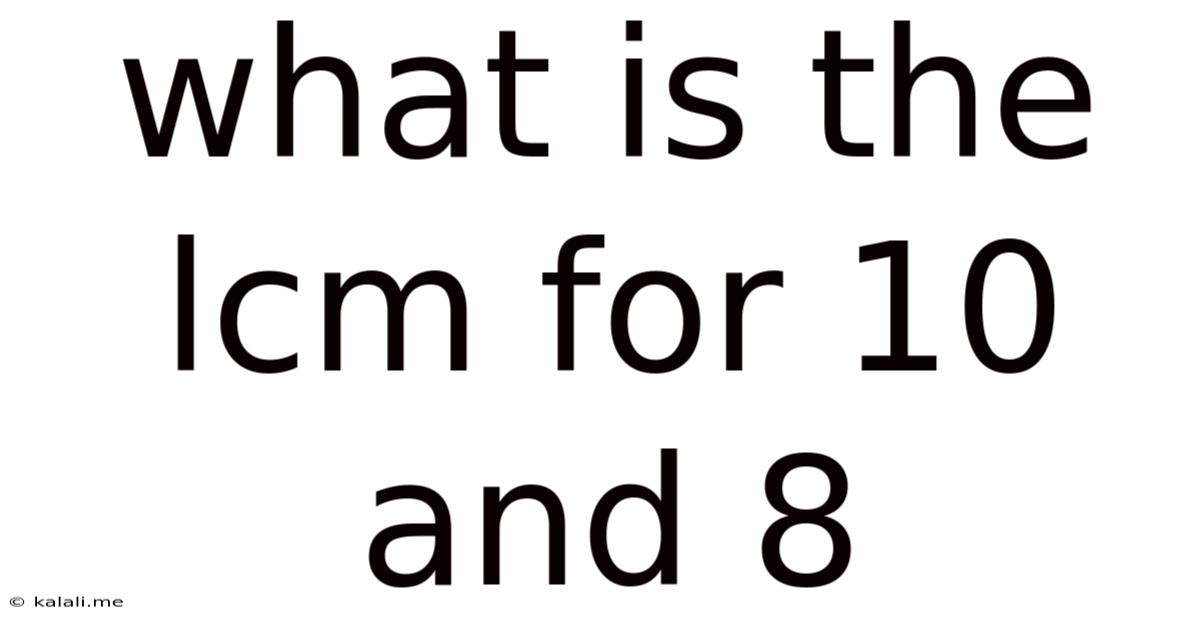
Table of Contents
What is the LCM for 10 and 8? A Deep Dive into Least Common Multiples
Finding the least common multiple (LCM) of two numbers might seem like a simple arithmetic problem, suitable only for elementary school students. However, understanding the LCM and its calculation methods is fundamental to various mathematical concepts and applications across diverse fields. This article will delve deep into determining the LCM of 10 and 8, exploring multiple approaches, and discussing the broader significance of LCM in mathematics and beyond. We'll uncover not just the answer, but the why behind the methods, making this more than just a simple calculation. This comprehensive guide will equip you with a solid understanding of LCM and its practical applications.
Meta Description: Learn how to calculate the least common multiple (LCM) of 10 and 8 using various methods. This in-depth guide explores different approaches, explains the underlying mathematical principles, and illustrates the importance of LCM in various applications.
Understanding Least Common Multiples (LCM)
Before we dive into calculating the LCM of 10 and 8, let's establish a clear understanding of what an LCM actually is. The least common multiple of two or more integers is the smallest positive integer that is divisible by all the integers without leaving a remainder. In simpler terms, it's the smallest number that contains all the numbers as factors. Think of it as the smallest common "measuring stick" that can accurately measure lengths related to all the given numbers.
For example, if we consider the numbers 2 and 3, their multiples are:
- Multiples of 2: 2, 4, 6, 8, 10, 12, 14, 16, 18...
- Multiples of 3: 3, 6, 9, 12, 15, 18, 21...
The common multiples are 6, 12, 18, and so on. The smallest of these common multiples is 6, therefore, the LCM of 2 and 3 is 6.
Method 1: Listing Multiples
The simplest method, suitable for smaller numbers, is to list the multiples of each number until a common multiple is found.
- Multiples of 10: 10, 20, 30, 40, 50, 60, 70, 80, 90, 100...
- Multiples of 8: 8, 16, 24, 32, 40, 48, 56, 64, 72, 80, 88, 96, 104...
By examining the lists, we can see that the smallest common multiple of 10 and 8 is 40.
This method is straightforward but becomes inefficient when dealing with larger numbers. Imagine trying to list the multiples of 144 and 252! It would be time-consuming and prone to error. Therefore, we need more efficient methods.
Method 2: Prime Factorization
This method leverages the fundamental theorem of arithmetic, which states that every integer greater than 1 can be uniquely represented as a product of prime numbers. This method is more efficient and scales better for larger numbers.
-
Find the prime factorization of each number:
- 10 = 2 × 5
- 8 = 2 × 2 × 2 = 2³
-
Identify the highest power of each prime factor present in the factorizations:
- The prime factors are 2 and 5.
- The highest power of 2 is 2³ = 8.
- The highest power of 5 is 5¹ = 5.
-
Multiply the highest powers of all prime factors together:
- LCM(10, 8) = 2³ × 5 = 8 × 5 = 40
This method is significantly more efficient, especially when dealing with larger numbers, as it avoids the tedious task of listing multiples.
Method 3: Using the Greatest Common Divisor (GCD)
The LCM and GCD (Greatest Common Divisor) of two numbers are related through a simple formula:
LCM(a, b) × GCD(a, b) = a × b
This means that if we know the GCD, we can easily calculate the LCM. Let's find the GCD of 10 and 8 using the Euclidean algorithm:
- Divide the larger number (10) by the smaller number (8): 10 ÷ 8 = 1 with a remainder of 2.
- Replace the larger number with the smaller number (8) and the smaller number with the remainder (2): 8 ÷ 2 = 4 with a remainder of 0.
- The GCD is the last non-zero remainder, which is 2.
Now, using the formula:
LCM(10, 8) = (10 × 8) / GCD(10, 8) = (80) / 2 = 40
This method is also efficient and particularly useful when dealing with larger numbers where prime factorization might be more computationally intensive.
Applications of LCM in Real Life
While finding the LCM of 10 and 8 might seem like a purely academic exercise, the concept of LCM has numerous practical applications:
-
Scheduling: Imagine two buses that depart from a bus station at different intervals. One bus departs every 10 minutes, and the other every 8 minutes. To find out when both buses will depart simultaneously, you need to calculate the LCM(10, 8) = 40. Both buses will depart together after 40 minutes.
-
Fractions: When adding or subtracting fractions with different denominators, finding the LCM of the denominators is crucial to find a common denominator.
-
Gear Ratios: In mechanical engineering, gear ratios often involve the LCM to determine the synchronization of rotating parts.
-
Music: The LCM is used in music theory to determine the least common multiple of note durations, helping synchronize musical rhythms.
-
Construction and Design: In construction and design, the LCM is often used in projects involving repeating patterns or cycles to determine the optimal spacing or timing.
-
Computer Science: The LCM concept plays a role in various algorithms and data structures, such as scheduling tasks in operating systems.
Beyond the Basics: LCM for More Than Two Numbers
The methods described above can be extended to find the LCM of more than two numbers. For prime factorization, you simply include all prime factors and their highest powers from all the numbers. For the GCD method, you'd need to iteratively calculate the GCD of pairs of numbers and then use the formula accordingly.
For example, to find the LCM of 10, 8, and 12:
-
Prime Factorization:
- 10 = 2 × 5
- 8 = 2³
- 12 = 2² × 3
-
Highest Powers:
- 2³ = 8
- 3¹ = 3
- 5¹ = 5
-
Multiply:
- LCM(10, 8, 12) = 2³ × 3 × 5 = 8 × 3 × 5 = 120
Therefore, the LCM of 10, 8, and 12 is 120.
Conclusion
Calculating the LCM, even for seemingly simple numbers like 10 and 8, provides a valuable opportunity to understand fundamental mathematical principles. This article has explored various methods for calculating the LCM, highlighting their strengths and weaknesses. Understanding the LCM is not merely an academic pursuit; it has significant practical implications across numerous fields, showcasing the power of seemingly basic mathematical concepts in solving real-world problems. Mastering these methods equips you with a powerful tool for tackling more complex mathematical challenges and opens doors to a deeper understanding of the interconnectedness of mathematical ideas. Remember, the core concept is finding the smallest number that's a multiple of all the given numbers – a concept with far-reaching applications beyond the classroom.
Latest Posts
Latest Posts
-
How Many Cups Of Chocolate Chips In 4 Oz
Jul 15, 2025
-
If Your 31 What Year Were You Born
Jul 15, 2025
-
How Many Tenths Are In An Inch
Jul 15, 2025
-
Which Word Has The Most Positive Connotation
Jul 15, 2025
-
How Do I Send An Evite Reminder
Jul 15, 2025
Related Post
Thank you for visiting our website which covers about What Is The Lcm For 10 And 8 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.